Закон всемирного тяготения. Сила тяжести

1. Силы, с которыми все тела притягиваются друг к другу, называют силами всемирного тяготения или гравитационными силами.

Закон всемирного тяготения был установлен Ньютоном, и он утверждает, что тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними.

​\( F=G\frac{m_1m_2}{r^2} \)​

где ​\( m_1 \)​ и ​\( m_2 \)​ — массы тел, ​\( r \)​ — расстояние между телами, ​\( G \)​ — постоянная всемирного тяготения или гравитационная постоянная.

Значение гравитационной постоянной установлено опытным путём, оно равно ​\( G \)​ = 6,67·10^-11 Нм²/кг². Смысл её заключается в следующем: два тела, каждое массой 1 кг, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой 6,67·10^-11 Н.

Значение гравитационной постоянной свидетельствует о том, что силы тяготения между телами малы. Они становятся заметными при больших значениях масс взаимодействующих тел. Например, притяжение шарика к Земле можно наблюдать без специальных приборов, а притяжение Земли к такому же шарику мы не можем наблюдать непосредственно.

Закон всемирного тяготения справедлив для тел, размерами которых можно пренебречь по сравнению с расстоянием между ними (для материальных точек). Закон применим также к шарам, в этом случае расстоянием между телами является расстояние между центрами шаров.

2. Все тела притягиваются к Земле. Силу притяжения тела к Земле называют силой тяжести ​\( (F_т) \)​.

По второму закону Ньютона сила равна произведению массы тела и ускорения, с которым оно движется под действием этой силы. Ускорение, с которым движется тело под действием силы тяжести, называется ускорением свободного падения и обозначается буквой ​\( g \)​. Ускорение свободного падения не зависит от массы тела. Соответственно, сила тяжести рассчитывается но формуле: ​\( F_т=mg \)​.

3. Закон всемирного тяготения позволяет получить формулу для вычисления значения ускорения свободного падения. С одной стороны, сила тяжести равна \( F_т=mg \), с другой стороны, сила притяжения тела к Земле может быть вычислена, исходя из закона всемирного тяготения: ​\( F_т=G\frac{M_Зm}{R^2} \)​, где ​\( M_З \)​ — масса Земли, ​\( m \)​ — масса тела, ​\( r \)​ — радиус Земли. Приравнивая правые части записанных равенств, получим: \( mg=G\frac{M_Зm}{R^2} \) или \( g=G\frac{M_З}{R^2} \).

Полученная формула позволяет вычислить ускорение свободного падения тела, находящегося на поверхности Земли. Она наглядно показывает, что значение ускорения свободного падения зависит от расстояния тела до центра Земли. Именно поэтому оно на экваторе больше, чем на полюсах.

По этой формуле можно вычислить ускорение свободного падения на любой планете, подставив вместо массы Земли массу соответствующей планеты, а вместо радиуса
Земли радиус планеты.

4. Если тело находится на высоте ​\( h \)​ относительно поверхности Земли, то ускорение свободного падения определяется равенством ​\( g=G\frac{M_З}{(R_З+h)^2} \)​. Из приведенного равенства понятно, что чем дальше тело находится от центра Земли, тем меньше ускорение свободного падения. Например, на высоте 18 км, на которой летают современные истребители, оно равно 9,72 м/с².

5. Пользуясь законом всемирного тяготения, можно вычислить скорость, которую необходимо сообщить телу для того, чтобы оно стало спутником Земли. Эта скорость
называется первой космической скоростью.

Центростремительное ускорение ​\( a \)​ спутнику массой ​\( m \)​ обеспечивает сила тяготения ​\( F_т \)​, которая по второму закону Ньютона равна ​\( F_т=ma \)​. Сила тяготения ​\( F_т=G\frac{M_Зm}{R^2} \)​, центростремительное ускорение равно ​\( a=\frac{v^2}{R} \)​, где ​\( v \)​ — линейная скорость спутника, ​\( R \)​ — радиус Земли. Откуда следует: ​\( G\frac{M_Зm}{R^2}=m\cdot\frac{v^2}{R} \)​ или ​\( g=\frac{v^2}{R} \)​. Отсюда ​\( v=\sqrt{gR} \)​, т.е. первая космическая скорость равна 7,9 км/с. Первый в мире искусственный спутник Земли был запущен в СССР в 1957 г.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Сила тяготения между двумя телами уменьшится в 2 раза, если массу каждого тела

1) увеличить в √2 раз
2) уменьшить в √2 раз
3) увеличить в 2 раза
4) уменьшить в 2 раза

2. Массу каждого из двух однородных шаров увеличили в 4 раза. Расстояние между ними тоже увеличили в 4 раза. Сила тяготения между ними

1) увеличилась в 64 раза
2) увеличилась в 16 раз
3) увеличилась в 4 раза
4) не изменилась

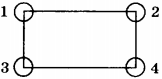
3. В вершинах прямоугольника расположены тела одинаковой массы. Со стороны какого тела на тело 1 действует наибольшая сила?

1) со стороны тела 2
2) со стороны тела 3
3) со стороны тела 4
4) со стороны всех тел одинаковая

4. Закон всемирного тяготения справедлив

A. Для всех тел
Б. Для однородных шаров
B. Для материальных точек

Правильный ответ

1) А
2) только Б
3) только В
4) и А, и Б

5. На ящик массой 5 кг, лежащий на полу лифта, движущегося с ускорением ​\( a \)​ вертикально вниз, действует сила тяжести

1) равная 50 Н
2) большая 50 Н
3) меньшая 50 Н
4) равная 5 Н

6. Сравните значения силы тяжести ​\( F_э \)​, действующей на груз на экваторе, с силой тяжести \( F_м \), действующей на этот же груз на широте Москвы, если груз находится на одной и той же высоте относительно поверхности Земли.

1) ​\( F_э=F_м \)​
2) \( F_э>F_м \)​
3) \( F_э<F_м \)​
4) ответ может быть любым в зависимости от массы тел

7. Сила тяжести, действующая на космонавта на поверхности Луны,

1) больше силы тяжести, действующей на него на поверхности Земли
2) меньше силы тяжести, действующей на него на поверхности Земли
3) равна силе тяжести, действующей на него на поверхности Земли
4) больше силы тяжести, действующей на него на поверхности Земли на экваторе, и меньше силы тяжести, действующей на него, на поверхности Земли на полюсе

8. Сила тяжести, действующая на тело, зависит от

А. Географической широты местности
Б. Скорости падения тела на поверхность Земли

Правильный ответ

1) только А
2) только Б
3) ни А, ни Б
4) и А, и Б

9. Какое(-ие) из утверждений верно(-ы)?

Сила тяжести, действующая на тело у поверхности некоторой планеты, зависит от

А. Массы планеты.
Б. Массы тела.

1) только А
2) только Б
3) ни А, ни Б
4) и А, и Б

10. Первая космическая скорость зависит

A. От радиуса планеты
Б. От массы планеты
B. От массы спутника

Правильный ответ

1) только А
2) только Б
3) только А и Б
4) А, Б, В

11. Установите соответствие между физической величиной (левый столбец) и формулой, выражающей её взаимосвязь с другими величинами (правый столбец). В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Сила тяжести
Б. Ускорение свободного падения на поверхности Земли
B. Закон всемирного тяготения

ФОРМУЛА
1) ​\( F=G\frac{m_1m_2}{r^2} \)​
2) ​\( F_т=mg \)​
3) ​\( g=G\frac{M_З}{(R_З+h)^2} \)​
4) ​\( g=G\frac{M_З}{R^2} \)​

12. Среди приведённых утверждений выберите два правильных и запишите их номера в таблицу

1) Гравитационная постоянная показывает, с какой силой притягиваются друг к другу два тела массой 1 кг.
2) Значение силы тяжести, действующей на тело, зависит от скорости его движения.
3) Ускорение свободного падения зависит от массы и радиуса планеты.
4) При увеличении расстояния между телами в 3 раза сила тяготения между ними уменьшается в 9 раз.
5) Изменение массы одного из взаимодействующих тел не влияет на значение силы тяготения.

Часть 2

13. Человек на Земле притягивается к ней с силой 700 Н. С какой силой он притягивался бы к Марсу, находясь на его поверхности, если радиус Марса в 2 раза меньше радиуса Земли, а масса в 10 раз меньше, чем масса Земли?

Ответы