Сила упругости. Вес тела

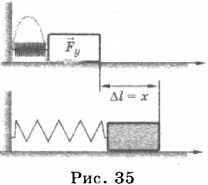
1. Твёрдые тела под действием силы способны изменять свои форму и (или) объём. Взяв за концы металлическую линейку, можно её согнуть. Если перестать прикладывать силу, то линейка восстановит свою форму. Если сжать пружину (рис. 35), то она сократится, т.е. деформируется. При прекращении действия силы пружина вернётся в первоначальное
состояние.

Изменение формы или объёма тела при действии на него силы называется деформацией.

Если длина пружины в недеформированном состоянии \( l_0 \), а после растяжения \( l \), то изменение её длины \( l=l-l_0=x \), где \( l \) или \( x \) – удлинение или деформация.

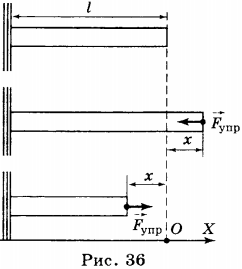
2. При деформации в теле возникает сила упругости, которая стремится вернуть его в первоначальное состояние. Сила упругости \( (\vec{F}_{упр}) \) — сила, возникающая в теле в результате деформации, стремящаяся вернуть тело в первоначальное состояние и направленная в сторону, противоположную деформации (удлинению).

Так, при растяжении пружины эта сила направлена влево к положению равновесия, при
сжатии пружины сила упругости направлена вправо (рис. 36).

Если тело после прекращения действия силы принимает первоначальную форму, то деформация является упругой. Если тело после прекращения действия силы не принимает первоначальную форму, то деформация является неупругой или пластической.

3. При малых деформациях сила упругости прямо пропорциональна удлинению. Поскольку сила упругости и деформация направлены в противоположные стороны, то: \( F_{упр}=-k\Delta l \), где \( k \) — коэффициент пропорциональности, называемый жёсткостью тела. Жёсткость зависит от размеров тела, его формы, материала, из которого сделано тело.

Единица жесткости \( [\,k\,]=\frac{[\,F\,]}{[\,\Delta l\,]} \); \( [\,k\,]=\frac{1\,Н}{1\,м}=1\frac{Н}{м} \).

Формула \( F_{упр}=-k\Delta l \) выражает закон Гука: сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению (деформации) тела и направлена в сторону, противоположную деформации.

Важно понимать, что закон Гука справедлив при малых деформациях.

На рисунке 37 приведён график зависимости модуля силы упругости от деформации. Поскольку эта зависимость линейная, то графиком зависимости является прямая, проходящая через начало координат и составляющая угол \( \alpha \) с осью абсцисс. По графику можно определить жёсткость тела. Например, значению деформации 2 см соответствует сила упругости 4 Н. Разделив 4 Н на 0,02 м, получим \( k \) = 200 Н/м. В треугольнике АОВ жёсткость \( k \) равна тангенсу угла \( \alpha \): \( k=\mathrm{tg}\alpha \).

4. Существуют разные виды деформации: растяжения, сжатия, сдвига, изгиба и кручения. В рассмотренных примерах линейка подвергалась деформации изгиба, пружина — деформации растяжения и сжатия, винты, гайки, болты при закручивании испытывают деформацию кручения, тяжёлые предметы при перемещении по полу — деформацию сдвига.

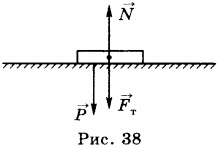
5. Предположим, что на полу стоит ящик (рис. 38). На него действует сила тяжести \( \vec{F}_т \), направленная вертикально вниз. Ящик, взаимодействуя с полом, деформирует его и деформируется сам. И на ящик, и на пол действует сила упругости, характеризующая их взаимодействие. Сила упругости \( \vec{N} \), действующая на ящик со стороны пола, приложена к ящику и направлена вертикально вверх; сила упругости \( \vec{P} \), действующая со стороны ящика на пол, приложена к полу и направлена вертикально вниз. Эта сила называется весом тела.

Весом тела называют силу, с которой тело, вследствие его притяжения к Земле, действует на опору или подвес. В отличие от силы тяжести, вес тела приложен не к телу, а к опоре или к подвесу. Вес — это сила упругости.

6. Если тело покоится или движется равномерно и прямолинейно, вес тела численно равен силе тяжести, действующей на него: \( \vec{P}=m\vec{g} \).

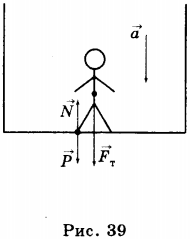
На тело, движущееся вместе с платформой или подвесом вертикально вниз с ускорением \( \vec{a} \), направленным в сторону движения, действуют сила тяжести \( \vec{F}_{т} \) и сила упругости \( N \) со стороны опоры или подвеса (рис. 39, 40).

Второй закон Ньютона для этой ситуации: \( m\vec{g}+\vec{N}=m\vec{a} \). В проекциях на координатную ось: \( mg-N=ma \) или \( N=mg-ma \). Поскольку \( N=P \), \( P = m(g — a) \).

Если тело движется вниз вместе с опорой или подвесом с ускорением, направленным так же, как и ускорение свободного падения, то его вес меньше силы тяжести, т.е. меньше веса покоящегося тела. Если ускорение тела равно ускорению свободного падения \( \vec{a}=\vec{g} \), то тело находится в состоянии невесомости.

В таком состоянии находится космонавт в космическом корабле, прыгун с трамплина во время полёта вниз.

7. На тело, движущееся вместе с платформой или подвесом вертикально вверх с ускорением \( \vec{a} \), направленным в сторону движения, действуют сила тяжести \( \vec{F}_т \) и сила упругости \( \vec{N} \) со стороны опоры или подвеса (рис. 40).

Второй закон Ньютона для этой ситуации: \( m\vec{g}+\vec{N}=m\vec{a} \). В проекциях на координатную ось: \( mg-N=-ma \) или \( N=mg+ma \). Поскольку \( N=P \), \( P=m(g+a) \).

Таким образом, если тело движется вверх вместе с опорой или подвесом с ускорением, направленным противоположно ускорению свободного падения, то его вес больше силы тяжести, т.е. больше веса покоящегося тела. Увеличение веса тела при движении с ускорением называют перегрузкой. Перегрузки испытывают космонавт в космическом корабле, пилот реактивного самолёта при взлёте и посадке.

Содержание

ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
Ответы

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Имеются две абсолютно упругие пружины. Под действием одной и той же силы первая пружина удлинилась на 8 см, а вторая — на 4 см. Сравните жёсткость \( k_2 \) второй пружины с жёсткостью \( k_1 \) первой пружины.

1) \( k_1=k_2 \)
2) \( 4k_1=k_2 \)
3) \( 2k_1=k_2 \)
4) \( k_1=2k_2 \)

2. Имеются две абсолютно упругие пружины: одна жёсткостью 200 Н/м, другая жёсткостью 400 Н/м. Сравните силу упругости \( F_2 \), возникающую во второй пружине, с силой упругости \( F_1 \), возникающей в первой пружине, при одинаковом их удлинении.

1) \( F_2=F_1 \)
2) \( F_2=4F_1 \)
3) \( 2F_2=F_1 \)
4) \( 0.5F_2=F_1 \)

3. Ученик, растягивая пружину динамометра последовательно на 1Н, 2Н, ЗН и 4Н, каждый раз измерял её удлинение и результаты измерений вносил в таблицу. Определите по данным таблицы жёсткость пружины динамометра.

1) 0,02 Н/м
2) 0,5 Н/м
3) 2 Н/м
4) 50 Н/м

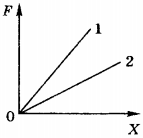
4. На рисунке приведены графики зависимости силы упругости от удлинения. Сравните жёсткость пружин.

1) \( k_2=k_1 \)
2) \( k_2>k_1 \)
3) \( k_2<k_1 \)
4) \( k_2\geq k_1 \)

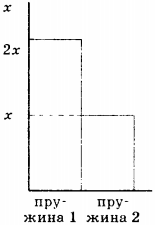
5. Учащийся выполнял эксперимент по измерению удлинения \( x \) пружин при подвешивании к ним грузов. Полученные учащимся результаты представлены на рисунке в виде диаграммы. Какой вывод о жёсткости пружин \( k_1 \) и \( k_2 \) можно сделать из анализа диаграммы, если к концам пружин были подвешены грузы одинаковой массы?

1) \( k_2=4k_1 \)
2) \( k_1=2k_2 \)
3) \( k_2=2k_1 \)
4) \( k_1=k_2 \)

6. Под действием силы 3 Н пружина удлинилась на 4 см. Чему равна сила, под действием которой удлинение этой пружины составит 6 см?

1) 3,5 Н
2) 4 Н
3) 4,5 Н
4) 5 Н

7. Две пружины растягиваются одинаковыми силами. Жёсткость первой пружины \( k_1 \) в 2 раза больше жесткости второй пружины \( k_2 \). Удлинение первой пружины \( \Delta l_1 \), удлинение второй пружины \( \Delta l_2 \) равно

1) \( 0.5\Delta l_1 \)
2) \( 0.67\Delta l_1 \)
3) \( 1.5\Delta l_1 \)
4) \( 2.5\Delta l_1 \)

8. В лифте, движущемся вниз равноускоренно из состояния покоя, стоит ящик. Модуль веса ящика

1) равен модулю силы тяжести
2) больше модуля силы тяжести
3) меньше модуля силы тяжести
4) увеличивается с увеличением скорости лифта

9. Человек испытывает перегрузки при

1) равномерном движении вниз
2) равномерном движении вверх
3) равноускоренном движении вверх из состояния покоя
4) равноускоренном движении вниз с ускорением свободного падения

10. Различие веса тела на экваторе и на полюсе можно обнаружить

А. Взвешивая тело на рычажных весах
Б. Взвешивая тело на пружинных весах

Правильный ответ

1)только А
2)только Б
3) и А, и Б
4) ни А, ни Б

11. Установите соответствие между физической величиной (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Модуль силы упругости пружины
Б. Жёсткость пружины
B. Модуль удлинения пружины

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) уменьшается
2) увеличивается
3) не изменяется

12. Из приведённых ниже высказываний выберите два верных и запишите их номера в таблицу.

1) Закон Гука справедлив при любых деформациях.
2) Сила упругости направлена в сторону, противоположную деформации.
3) Жёсткость зависит только от материала, из которого изготовлено тело.
4) Вес тела всегда равен действующей на него силе тяжести.
5) Вес приложен к опоре или к подвесу.