Глава 8. Выполняем работу

В этой главе…
- Приглядываемся к работе силы
- Изучаем отрицательную работу
- Оцениваем кинетическую энергию
- Приобретаем потенциальную энергию
- Постигаем консервативные и неконсервативные силы
- Вычисляем механическую энергию и мощность
С работой в обыденном смысле мы сталкиваемся всякий раз, например, когда приходится решать задачи по физике. Нужно брать книги, калькулятор, бумагу с ручкой, а потом потеть и корпеть над задачей. После получения решения мы выполнили вполне определенную работу, но… совсем не в том смысле, в котором термин “работа” определяется в физике.
В физике работой называется произведение прилагаемой силы и перемещения, выполняемого этой силой. Помимо понятия “работа” в этой главе рассматриваются связанные с ней понятия потенциальной и кинетической энергии, консервативной и неконсервативной силы, а также механической энергии и мощности. Пора приступать к… работе!
Содержание
- Работа: не совсем то, о чем вы подумали
- Работаем в разных системах единиц измерения
- Толкаем груз
- Тянем груз под углом
- Выполняем отрицательную работу
- Получаем компенсацию в виде кинетической энергии
- Сохраняем энергию: потенциальная энергия
- Выбираем путь: консервативные и неконсервативные силы
- Как ни крути, а энергия сохраняется
- Мощность: ускоряем темп работы
Работа: не совсем то, о чем вы подумали
Итак, работа \( W \) — это произведение прилагаемой силы \( \mathbf{F} \) и перемещения \( \mathbf{s} \), выполняемого этой силой. Точнее говоря речь идет о проекции прилагаемой силы на направление перемещения, т.е. \( W=Fs\cos\theta \), где \( \theta \) — угол между векторами силы \( \mathbf{F} \) и перемещения \( \mathbf{s} \). С точки зрения физика, работа равна произведению компоненты силы в направлении перемещения и величины перемещения.
Прежде чем переходить к подробному рассмотрению особенностей работы, познакомимся с единицами измерения работы в разных системах единиц измерения.
Работаем в разных системах единиц измерения
Работа является скалярной, а не векторной величиной, т.е. она имеет величину, но не имеет направления (подробнее скаляры и векторы рассматриваются в главе 4). Согласно формуле \( W=Fs\cos\theta \), работа измеряется в единицах “Н·м” в системе СИ или в единицах “г·см2/с2” — в системе СГС. Но с такими единицами не очень удобно работать, и физики для измерения работы используют специальную единицу измерения — джоуль (или сокращенно Дж) в системе СИ. Иначе говоря, в системе СИ 1 Дж = 1 Н · 1 м.
В системе СГС работа измеряется в единицах “г·см2/с2”. Вместо нее для удобства физики также используют специальную единицу измерения — эрг (неплохое название для единицы работы, поскольку очень похоже на энергичное междометие, произнесенное во время подъема тяжелого груза). Иначе говоря, 1 эрг = 1 дин · 1 см. В системе фут-фунт-секунда работа измеряется в единицах “фунт-фут”. (Эти системы единиц подробно описываются в главе 2 .)
Толкаем груз
Не такая уж и легкая работа — держать тяжелый груз, например большие гантели, на вытянутых вверх руках. Однако с точки зрения физики, несмотря на приложенную силу, здесь нет никакого перемещения, а значит, нет и работы. Хотя с точки зрения биологии здесь выполняется огромная работа, но с точки зрения физики работы нет, если нет перемещения. Даже с точки зрения химии наше тело поставляет огромное количество энергии нашим мышцам для удержания груза. Но, несмотря на очевидную физическую усталость, работа с точки зрения физики не выполняется.
Для работы необходимо движение. Представьте, что вы нашли огромный слиток золота и толкаете его домой, как показано на рис. 8.1. Какую работу придется при этом выполнить? Во-первых, нужно определить силу, которую нужно приложить к слитку.
Пусть коэффициент трения скольжения, \( \mu_c \) (подробнее об этом см. главу 6), между поверхностями слитка и дороги равен 0,25, а слиток имеет массу 1000 кг. Итак, какую силу нужно приложить к слитку, чтобы поддерживать его движение вопреки силе трения скольжения \( F_{трение} \)? Начнем поиск ответа на этот вопрос со следующей формулы, известной нам из главы 6:
где \( F_н \) — это нормальная сила.
Предполагая, что поверхность дороги абсолютно плоская, получим, что нормальная сила \( F_н \) равна произведению массы слитка \( m \) на ускорение свободного падения \( g \) под действием силы гравитационного притяжения (силы тяжести) между слитком и Землей:
Подставляя численные значения, получим:
Итак, для преодоления силы кинетического трения нужно приложить силу 2450 Н. Допустим, что длина пути до вашего дома равна 3 км. Какую работу придется проделать, чтобы дотолкать этот слиток золота домой? Поскольку угол \( \theta \) между направлением прилагаемой силы \( \mathbf{F} \) и перемещением \( \mathbf{s} \), выполняемым под действием этой силы, равен нулю, то формула работы \( W=Fs\cos\theta \) упрощается, поскольку \( \cos\theta \) = 1. Подставляя численные значения, получим:
Итак, потребуется выполнить работу, равную 7,35·106 Дж, чтобы дотолкать этот слиток золота домой. Насколько это много? Чтобы поднять груз массой 1 кг на высоту 1 м, требуется выполнить работу около 9,8 Дж. Теперь понятно: чтобы дотолкать слиток золота домой, потребуется выполнить приблизительно в 750 тыс. раз большую работу.
Работу измеряют также в калориях (или сокращенно кал), причем 1 кал = 4,186 Дж. Эту единицу измерения используют также для измерения энергии, и ее часто можно встретить на упаковках продуктов питания. Так вот, чтобы дотолкать слиток золота домой, вам потребуется потратить 1,755·106 калорий, или 1755 Ккал (т.е. килокалорий, где 1 килокалория = 1 Ккал). Забегая вперед, скажем, что в электротехнике для измерения работы и энергии используется единица “киловатт·час” (кВт·ч), которая равна 3,6·106 Дж. Итак, для выполнения этой работы потребуется около 2 кВт·ч. (Более подробно эти и другие единицы измерения описываются в конце этой главы и в главе 13.)
Тянем груз под углом
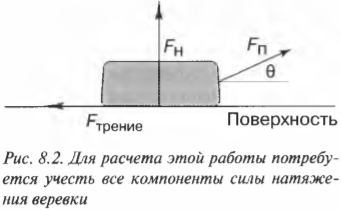
А может, попробовать не толкать, а тянуть слиток золота с помощью веревки, как показано на рис. 8.2?
Поскольку веревка направлена под углом \( \theta \) к направлению перемещения, то нам для вычисления работы придется использовать формулу:
где \( F_{натяжение} \) — это сила натяжения веревки.
Допустим, что нить привязана к центру слитка. Поскольку вертикальная компонента силы натяжения веревки \( F_{натяжение}\sin\theta \) направлена вверх, то она частично компенсирует нормальную силу. В конечном итоге вертикальная компонента силы натяжения веревки \( F_{натяжение}\sin\theta \) уменьшает силу трения:
Для перемещения слитка в данном случае горизонтальная компонента силы натяжения \( F_{натяжение}\cos\theta \) должна компенсировать силу трения:
Из двух последних соотношений получаем, что:
и необходимая сила натяжения веревки равна:
В предыдущем примере (где прилагаемая сила не имела наклона) прилагаемая сила компенсировала силу трения \( F_{натяжение(прежнее)}=\mu_cmg \) и была равна 2450 Н.
Следовательно, теперь необходимая сила натяжения веревки равна:
(Обратите внимание на следующие интересные особенности использования веревки, которую тянут под углом к горизонтали. Во-первых, при наклоне 10° потребуется приложить меньшую силу, чем при толкании слитка без наклона. Во-вторых, минимальное значение силы натяжения веревки достигается при максимальном значении знаменателя \( \mu_c\sin\theta+\cos\theta \), когда \( \mu_c=tg\,\theta \), т.е. для \( \mu_c \) = 0,25 при угле \( \theta \) ≈ 14°, а сама минимальная сила натяжения веревки равна 2376 Н. — Примеч. ред.)
Выполняем отрицательную работу
Представьте себе, что вы купили огромный телевизор массой 100 кг, вам нужно поднять его с пола и занести его наверх по ступенькам, поднимая приблизительно на высоту около 0,5 м. Какую работу нужно выполнить, если предполагается, что ее придется выполнять для преодоления силы тяжести \( F=mg \), где \( m \) — это масса телевизора, a \( g \) — ускорение свободного падения?
В таком случае работа равна:
Допустим, что груз оказался слишком тяжелым (не удивительно, ведь телевизор весит 100 кг!) и его пришлось опустить снова на пол. Какую работу нужно выполнить, чтобы опустить телевизор? Верите или нет, но эта работа будет отрицательной! Действительно, теперь вектор силы направлен противоположно вектору перемещения, т.е. угол между этими векторами \( \theta \) = 180°, a \( \cos \)180° = -1.
Поэтому в этом случае работа равна:
Общая работа \( W=W_1+W_2=0 \). Нулевая работа? Да, с точки зрения физики общая работа в этом случае равна нулю.
Если компонента вектора силы направлена в том же направлении, что и компонента вектора перемещения, то работа будет положительной. А если они направлены в противоположные стороны, то работа будет отрицательной.
Получаем компенсацию в виде кинетической энергии
Если сила, приложенная к объекту, больше силы сопротивления, например силы трения или силы тяжести, то результирующая сила приводит объект в движение. Соответствующая работа этой силы приводит к увеличению скорости объекта, т.е. увеличению его энергии движения или, иначе говоря — кинетической энергии. Здесь кинетической энергией называется способность объекта совершать некую работу за счет энергии его движения.
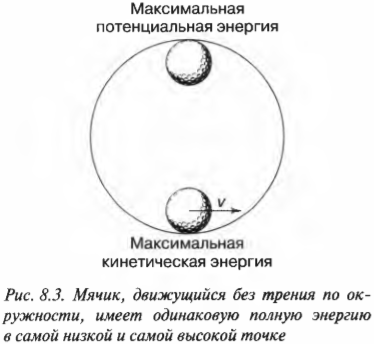
Представьте себе мячик для игры в гольф, который движется по окружности, как показано на рис. 8.3. Причем в самой нижней точке траектории скорость мячика максимальна, а в самой верхней точке — минимальна, например равна нулю. С точки зрения физики в самой нижней точке траектории мячик имеет бОльшую кинетическую энергию, чем в самой верхней точке, где она равна нулю. Куда пропадает и откуда снова берется кинетическая энергия при периодическом вращательном движении по этой траектории?
На самом деле энергия никуда не пропадает и ниоткуда не берется. Она просто переходит из одной формы в другую. В самой высокой точке энергия переходит из кинетической формы в потенциальную, а в самой нижней — наоборот, из потенциальной формы в кинетическую. Потенциальной энергией называется способность объекта совершить работу при изменении его координат под действием силы, т.е. в данном случае при перемещении вниз под действием силы тяжести. (Более подробно потенциальная энергия описывается далее в этой главе.)
Допустим, что в самой нижней точке траектории мячик имеет кинетическую энергию 20 Дж. В самой верхней точке кинетическая энергия равна 0 Дж. В таких случаях говорят, что 20 Дж кинетической энергии преобразуется в 20 Дж потенциальной энергии. А в самой нижней точке наоборот: 20 Дж потенциальной энергии преобразуется в 20 Дж кинетической энергии. Такое взаимное превращение энергии из одной формы в другую без потерь называется законом сохранения энергии. (Более подробно он описывается далее.)
А что происходит с кинетической энергией при наличии силы трения, как в предыдущем примере со слитком на горизонтальной плоскости? Если на движущийся слиток не действует никакая движущая сила, то его скорость постепенно уменьшается. Дело в том, что его кинетическая энергия рассеивается на нагрев соприкасающихся поверхностей объекта и плоскости.
Итак, после предварительного знакомства с превращениями энергии попробуем подсчитать ее величину.
Запоминаем формулу кинетической энергии
Работа по ускорению объекта тратится на увеличение его скорости или, как говорят физики, на увеличение кинетической энергии:
Кинетическую энергию \( K \) можно легко вычислить, зная массу \( m \) и скорость \( v \) объекта.
Как получить связь между кинетической энергией и работой? Как известно, связь между силой и ускорением имеет вид:
Работа силы при перемещении объекта равна:
Предположим, что сила прилагается в том же направлении, в котором происходит перемещение объекта (\( \cos\theta \) = 1), то есть:
Из главы 3 нам известно следующее соотношение между начальной \( v_1 \) и конечной \( v_2 \) скоростями объекта, перемещающегося с ускорением \( a \) на расстояние \( s \):
Иначе говоря, получаем:
Подставляя это соотношение для ускорения в формулу для работы, получим:
Используем соотношение для кинетической энергии
Попробуем определить кинетическую энергию пули с массой 10 г, которая вылетает из ствола пистолета со скоростью 600 м/с. Зная формулу кинетической энергии, подставим в нее численные значения (не забудьте преобразовать 10 грамм в 0,01 килограмма) и получим:
Маленькая пуля массой всего 10 г обладает очень большой энергией 1800 Дж.
Выражение для кинетической энергии можно применять для вычисления скорости, приобретенной объектом после выполнения некоторой работы по его ускорению. Предположим, что вы находитесь в космическом корабле на околоземной орбите и должны запустить искусственный спутник. Нужно открыть створки грузового отсека вашего космического корабля, выгрузить спутник массой 1000 кг и выполнить работу, прилагая силу 2000 Н на расстоянии 1 м. Какую скорость приобретет спутник в результате этой работы?
Как известно, работа определяется следующей формулой:
Поскольку сила прилагается в том же направлении, в котором происходит перемещение спутника (\( \cos\theta \) = 1), то:
Подставляя численные значения, получим:
Эта работа приводит к разгону спутника, т.е. работа преобразуется в кинетическую энергию спутника:
Отсюда легко можно определить искомую скорость спутника:
Такой будет скорость спутника относительно космического корабля.
Учтите, что работа может иметь и отрицательный знак, если, например, нужно затормозить движущийся спутник. Действительно, для этого придется приложить силу, направленную против перемещения. В этом случае приращение кинетической энергии спутника также будет иметь отрицательную величину.
В этом примере мы учли только одну силу, а в реальном мире на любой объект действует сразу несколько сил.
Вычисляем кинетическую энергию объекта по результирующей силе
Допустим, что вам нужно найти общую работу всех сил, приложенных к объекту, и определить полученную кинетическую энергию объекта. В примере из главы 6 со слитком на наклонной плоскости на слиток в направлении, перпендикулярном к наклонной плоскости, действуют нормальная сила и компонента силы тяжести. Обе эти силы компенсируют друг друга в этом направлении. Слиток не перемещается в направлении, перпендикулярном к наклонной плоскости. Это значит, что эти две силы не выполняют работу и не придают слитку кинетическую энергию.
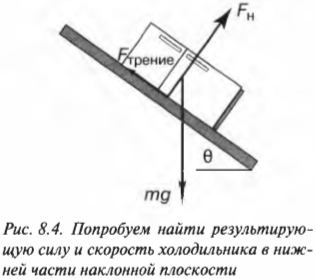
На рис. 8.4 показан уже знакомый нам пример с холодильником на наклонной плоскости. Допустим, что холодильник нужно спустить по наклонной плоскости, удерживая его с помощью каната с силой натяжения \( F_н \). Попробуем с помощью формул работы результирующей силы и кинетической энергии определить скорость холодильника в самом конце наклонной плоскости.
Какова результирующая сила, которая действует на холодильник? Из главы 6 мы уже знаем, что компонента силы тяжести вдоль наклонной плоскости равна:
где \( m \) — это масса холодильника, a \( g \) — ускорение свободного падения. Нормальная сила (см. главу 6) равна:
А сила трения скольжения (см. главу 6) равна:
где \( \mu_c \) — коэффициент трения скольжения. Результирующая сила \( F_{рез} \) направлена вдоль наклонной поверхности и равна:
Большая часть пути пройдена! Если угол наклона плоскости \( \theta \) = 30°, а коэффициент трения скольжения \( \mu_c \) = 0,15, то, подставляя численные значения, получим:
Итак, результирующая сила, которая действует на холодильник, равна 363 Н. Она действует на всем протяжении наклонной плоскости, т.е. 3 м, и совершаемая ею работу равна:
Если вся эта работа тратится на ускорение холодильника, то она преобразуется в кинетическую энергию, то есть:
Отсюда легко найти финальную скорость холодильника:
Итак, в конце наклонной плоскости холодильник будет иметь скорость 4,67 м/с.
Сохраняем энергию: потенциальная энергия
Объекты могут обладать не только энергией движения, т.е. кинетической энергией, но и энергией положения, т.е. потенциальной энергией. Эта энергия имеет такое название потому, что может быть преобразована (т.е. имеет потенциал преобразования) в кинетическую или другую энергию.
Представьте себе, что вы катаете с горки маленького ребенка. Для подъема на горку вам придется совершить определенную работу. Чем выше стартовая позиция малыша, тем большую скорость он приобретает в конце горки. Выше, еще выше, еще выше… Обычно на каком-то из этих этапов эксперименты решительно прекращается взволнованной мамой малыша.
Что же происходило на горке (до появления мамы)? Откуда возникла кинетическая скорость малыша? Она произошла от работы против силы тяжести, которую вы совершили по подъему малыша на горку. Действительно, малыш, сидя в стартовой позиции в верхней части горки, обладает нулевой скоростью и нулевой кинетической энергией. Выполнив работу против силы тяжести по подъему малыша наверх, вы тем самым увеличили его (и свою) потенциальную энергию. И только после спуска вниз под действием силы тяжести малыш приобретает кинетическую энергию в результате преобразования этой потенциальной энергии.
Работа против силы тяжести
Какую работу нужно выполнить против силы тяжести? Допустим, что вам нужно переместить тяжелое ядро с пола на верхнюю полку на высоту \( h \). Необходимая для этого работа \( W \) силы \( \mathbf{F} \) при перемещении на расстояние \( \mathbf{s} \) при угле между их векторами \( \theta \) выражается формулой:
В данном случае сила тяжести \( \mathbf{F = mg} \), а угол \( \theta \) между векторами \( \mathbf{F} \) и \( \mathbf{s} \) можно выразить с помощью разности высот \( h=s\cos\theta \) между полом и верхней полкой.
Таким образом, работа против силы тяжести по перемещению тяжелого ядра с пола на верхнюю полку на высоту \( h \) равна:
Если ядро упадет с верхней полки на пол, то какую скорость оно разовьет, т.е. какую кинетическую энергию приобретет ядро? Запомните: оно приобретет кинетическую энергию, равную разнице потенциальных энергий, т.е. \( mgh \). Это значит, что затраченная работа на подъем ядра преобразуется в кинетическую энергию в точке соприкосновения ядра с полом.
Вообще говоря, объект с массой \( m \) вблизи поверхности Земли, где ускорение свободного падения \( g \) постоянно, при перемещении вверх на высоту \( h \) приобретает потенциальную энергию \( U \), равную \( mgh \). Если вы перемещаете объект вертикально против силы тяжести с высоты \( h_0 \) на высоту \( h_1 \) то изменение его потенциальной энергии равно:
Работа по преодолению силы тяжести тратится на увеличение потенциальной энергии объекта.
Преобразуем потенциальную энергию в кинетическую
Объект может характеризоваться разными видами потенциальной энергии в зависимости от типа сил, которые действуют на него. Действительно, работа может выполняться не только против силы тяжести, но, например, и против силы упругости пружины. Однако в задачах по физике источником потенциальной энергии чаще всего является сила тяжести. В этом случае на поверхности Земли потенциальную энергию принято считать равной нулю, а этот уровень потенциальной энергии называют нулевым. Тогда говорят, что на высоте \( h \) объект с массой \( m \) обладает потенциальной энергией \( mgh \).
Допустим, что ядро с массой 40 кг падает с высоты 3 м на пол. Какую скорость оно приобретет при касании с полом? В данном случае его потенциальная энергия \( U \), равная
преобразуется в кинетическую \( K \), т.е.:
Поэтому, используя сведения из предыдущего раздела, можно вычислить финальную скорость в момент касания пола:
Подставляя численные значения, получим:
Падающее на пол ядро с массой 40 кг и скоростью 7,67 м/с — это впечатляющее зрелище, но не совсем приятное, если на пути ядра находится ваша нога. Учтите это и постарайтесь не допустить нежелательной встречи.
Выбираем путь: консервативные и неконсервативные силы
Если работа силы при перемещении объекта определяется только начальной и конечной координатами объекта и не зависит от траектории перемещения, то такая сила называется консервативной. Примером консервативной силы является сила гравитационного притяжения. А сила трения не является такой, поскольку совершаемая ею работа зависит от траектории перемещения. Сила трения является неконсервативной.
Допустим, что две группы друзей решили покорить небольшую гору высотой \( h_1 \) стартуя с места на высоте \( h_0 \). Одна группа пошла коротким и крутым путем, а другая — длинным, но более пологим и живописным. Обе группы встретились наверху и решили сравнить увеличение потенциальной энергии \( \Delta{U} \). “Наша потенциальная энергия увеличилась на \( mg(h_1-h_0) \)”, — сказали одни. “Наша потенциальная энергия тоже увеличилась на \( mg(h_1-h_0) \)”, — ответили другие.
Действительно, согласно рассуждениям в прежнем разделе, изменение потенциальной энергии выражается следующей формулой:
Это уравнение фактически означает, что независимо от выбранного пути на вершину горы, на увеличение потенциальной энергии путников влияет только разница между высотой исходной точки \( h_0 \) и высотой вершины \( h_1 \). Именно потому, что работа против силы гравитационного притяжения не зависит от выбранного пути, эта сила является консервативной силой.
А вот еще один пример проявления консервативности силы тяжести. Предположим, что вы отдыхаете в отеле в одной из горных деревушек в Альпах и решили прогуляться на машине по долине, а затем по близлежащим перевалам и горным вершинам. За день вы множество раз совершали спуск и подъем, а к вечеру вернулись к исходному месту — к своему отелю. Чему в итоге равно изменение вашей потенциальной энергии? Иначе говоря, каков результат всей дневной работы против силы тяжести? Ответ прост: поскольку сила тяжести является консервативной и вы вернулись в исходную точку, то изменение потенциальной энергии равно 0. Результирующая работа против силы тяжести равна 0.
Конечно, на всем пути со стороны дороги на автомобиль действовала нормальная сила, но она всегда направлена перпендикулярно дороге и перемещению, а потому не совершает работы.
С консервативными силами удобно работать, поскольку они не допускают “утечки” энергии вдоль замкнутого пути перемещения, когда конечная точка перемещения совпадает с исходной (работа консервативных сил по замкнутому пути равна нулю). Однако все гораздо сложнее с такими силами, как сила трения скольжения или сила сопротивления воздуха. Если тянуть тяжелый груз по шершавой поверхности, то работа против сил трения будет очень сильно зависеть от выбранного пути и не будет равной нулю для замкнутого пути. В этом случае мы имеем дело с неконсервативной силой, работа против которой зависит от выбранного пути.
Рассмотрим подробнее силу трения, как типичный пример неконсервативной силы. При совершении работы против силы трения происходит “утечка” механической энергии объекта, которая объединяет кинетическую и потенциальную энергии. При совершении работы при перемещении объекта с трением часть работы рассеивается в виде тепла. Забегая вперед, следует сказать, что закон сохранения полной энергии при этом не нарушается, если учесть преобразование части работы в тепловую энергию.
Как ни крути, а энергия сохраняется
Механической энергией называется сумма потенциальной и кинетической энергии объекта. Благодаря закону сохранения этой полной механической энергии, процедура решения задач по физике существенно упрощается. Рассмотрим поподробнее этот закон.
Пусть тележка на аттракционе “Американские горки” в разных точках 1 и 2 на разных высотах \( h_1 \) и \( h_2 \) имеет разные скорости \( v_1 \) и \( v_2 \). Полная механическая энергия тележки \( E_1 \) в точке 1 равна:
а полная механическая энергия тележки \( E_2 \) в точке 2 равна:
Чему равна разница между величинами \( E_1 \) и \( E_2 \). При наличии неконсервативных сил эта разница должна быть равна работе \( W_{неконс} \) этих сил
С другой стороны, если неконсервативные силы отсутствуют, т.е. \( W_{неконс} \) = 0, то:
или:
или:
Именно эти равенства представляют собой закон сохранения механической энергии. Если работа неконсервативных сил равна нулю, то полная механическая энергия сохраняется. (Закон сохранения механической энергии гласит, что при наличии консервативных сил полная энергия остается неизменной, а могут происходить только превращения потенциальной энергии в кинетическую и обратно. — Примеч. ред.)
Иногда удобно сократить массу \( m \) в следующей формулировке закона сохранения энергии:
и использовать более простую формулировку:
Определяем конечную скорость с помощью закона сохранения энергии
Совсем непросто проводить физические эксперименты на аттракционе “Американские горки”. Но ведь кто-то должен их делать! Представьте себе, что вы находитесь в тележке, которая практически без трения скользит по рельсам вниз с высоты \( h_1 \) = 400 м. Предположим, что где-то на полпути вниз выходит из строя спидометр и уже нельзя определить скорость тележки по приборам. Как вычислить скорость \( v_2 \) в самой нижней точке спуска \( h_2 \)? Нет проблем. Все, что нам нужно, это закон сохранения энергии. Согласно этому закону, полная механическая энергия объекта должна сохраняться, если равна нулю работа всех неконсервативных сил. Из предыдущего раздела нам уже знакома следующая сокращенная формулировка закона сохранения энергии:
Для простоты предположим, что начальная скорость \( v_1 \) = 0, а высота самой нижней точки спуска \( h_2 \) = 0. Тогда предыдущее уравнение существенно упрощается:
Откуда очень легко получить формулу для конечной скорости:
Подставляя численные значения, получим:
Итак, скорость тележки в самой нижней точке спуска на аттракционе “Американские горки” будет равна 89 м/с или около 320 км/ч. Довольно быстро: дух перехватит даже у самых отчаянных смельчаков!
Определяем максимальную высоту подъема с помощью закона сохранения энергии
Помимо определения конечной скорости, с помощью закона сохранения энергии можно также определить максимальную высоту подъема. Предположим, что Тарзан находится у кишащей крокодилами реки и хочет с помощью гибкой лианы перепрыгнуть с низкого берега на другой более высокий берег, высота которого на 9 м больше. Пусть максимальная скорость \( v_1 \), с которой он может разогнаться на низком берегу (т.е. в самой нижней точке траектории), равна 13 м/с. Достаточно ли этой скорости, чтобы запрыгнуть на противоположный высокий берег? Попробуем применить известную нам сокращенную формулировку закона сохранения энергии:
Предположим, что высота начального положения \( h_1 \) = 0. Чтобы определить максимально возможную высоту конечного положения на другом высоком берегу, следует предположить, что конечная скорость \( v_2 \) = 0. При таких условиях прежняя формула существенно упрощается:
Отсюда очень легко получить формулу для высоты конечного положения \( h_2 \) на другом берегу:
Подставляя численные значения, получим:
Итак, Тарзану не хватит 40 см, чтобы с максимальной скоростью разгона 13 м/с запрыгнуть на другой берег с помощью лианы.
Мощность: ускоряем темп работы
Иногда нужно знать не только объем работы, но и темп, с которым она выполняется. Скорость выполнения работы за единицу времени называется мощностью. Она выражается следующей простой формулой:
где \( W \) — это работа, выполненная за время \( t \).
В качестве примера рассмотрим два гоночных катера, способных развивать скорость до 200 км/ч. Какой из них обладает более мощным мотором? Конечно тот, который быстрее разгоняется до максимальной скорости, т.е. быстрее проделывает одинаковую работу по ускорению катера.
Если с течением времени скорость выполнения работы меняется, то в таких случаях часто используют понятие средней мощности, т.е. отношения всей выполненной работы \( W \) за все время \( t \):
Усредненные величины в физике принято обозначать знаком подчеркивания над соответствующей величиной. Прежде, чем приступать к применению понятии мощности, следует познакомиться с единицами измерения мощности.
Единицы измерения мощности
Поскольку мощность— это работа за единицу времени, то единицей измерения мощности является Дж/с, т.е. единица работы (джоуль), деленная на единицу времени (секунда), или ватт (Вт).
Обратите внимание, что поскольку работа и время являются скалярными величинами (подробнее о скалярах рассказывается в главе 4), то и мощность является скалярной величиной. Кроме ватта, для измерения мощности по историческим причинам часто используется единица “лошадиная сила” (л.с.), которая приблизительно равна 745,7 Вт. (Физики очень редко пользуются этой единицей из-за ее неоднозначного определения. Например, в метрической системе единиц измерения она равна 735,49875 Вт и получила название “метрической” лошадиной силы, а в английской системе единиц измерения — 745,6998 Вт и более известна под названием “механической” лошадиной силы. Кроме того, существуют “электрическая” (746 Вт) и даже “бойлерная” (9810 Вт) лошадиные силы. Однако, несмотря на эти различия, по историческим причинам единица “лошадиная сила” получила широкое распространение, особенно в автомобильной промышленности. — Примеч. ред.)
Предположим, что среднестатистическая лошадь массой \( m_л \) = 500 кг способна разогнать себя и санки массой \( m_с \) = 500 кг от скорости \( v_1 \) = 1 м/с до скорости \( v_2 \) = 2 м/с за время \( t \) = 2 с. Какой мощностью обладает эта лошадь? Берем формулу работы:
и, подставляя в нее эти значения, получим:
А теперь, зная работу, вычислим мощность лошади:
Совсем неплохо для среднестатистической лошади иметь мощность чуть больше 1 л.с.!
Вычисляем мощность другими способами
Поскольку работа равна произведению силы и времени, то формулу для мощности можно записать следующим образом:
Однако скорость \( v = s/t \), и потому:
Интересный результат, не так ли? Оказывается, что мощность равна произведению скорости и силы. Аналогичную формулу можно использовать и для вычисления средней мощности \( \overline{P} \) , если прикладываемая сила \( F \) постоянна:






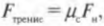
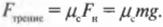
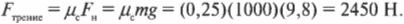
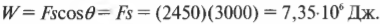

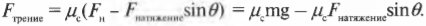
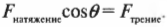
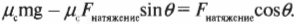
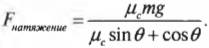
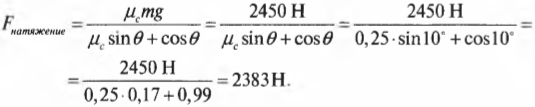
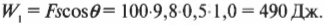
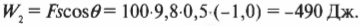
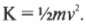
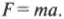
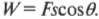
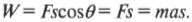
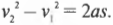
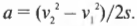
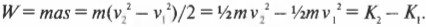
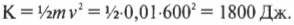
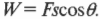
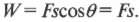
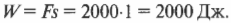
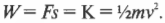
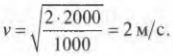
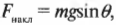
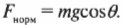
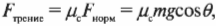
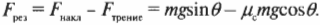
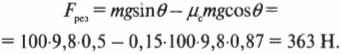
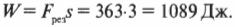

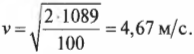
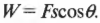
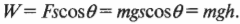
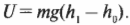
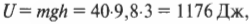
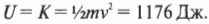
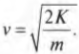
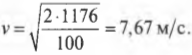
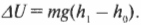
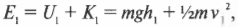
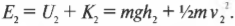
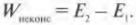

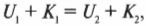
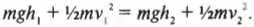
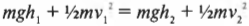
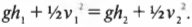
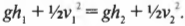
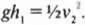
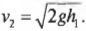
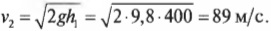
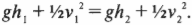
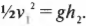
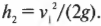
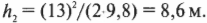
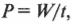
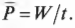
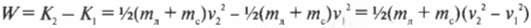
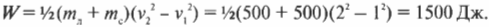
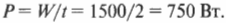
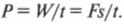
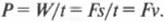
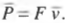
Добавить комментарий