Глава 9. Двигаем объекты: количество движения и импульс
В этой главе…
- Измеряем количество движения
- Вычисляем импульс
- Выясняем связь между силой и изменением импульса
- Разбираемся с законом сохранения импульса
- Знакомимся с разными типами столкновений
Эта глава посвящена понятиям, которые следует учитывать при изучении движения объектов, а именно с импульсом и моментом импульса. Оба эти понятия играют большую роль в двух разделах механики: кинематике, посвященной изучению движения объектов, и динамике, посвященной изучению взаимодействия объектов. Владея этими понятиями, можно легко описывать поведение объектов при столкновениях: с какой скоростью продолжат движение сталкивающиеся объекты (не хотелось бы, чтобы на их месте были ваш автомобиль или велосипед), в каком направлении продолжит движение теннисный мячик после столкновения с ракеткой, насколько глубоко дротик для игры в дартс вонзится в мишень и т.п. Чтобы получить ответы на эти и многие другие вопросы, нужно очень хорошо представлять себе, что такое импульс и момент импульса. Описанию именно этих понятий и посвящается данная глава.
Содержание
- Изучаем количество движения
- Получаем импульс
- Связываем работу силы и изменение импульса
- Изучаем закон сохранения импульса
- Упругие и неупругие столкновения
Изучаем количество движения
В физике импульсом называется количество движения, которое приобретает тело под действием заданной силы за определенное время. Играя в бильярд, нетрудно убедиться в разнообразных проявлениях импульса. Чем сильнее и быстрее удар кия по шару, тем интенсивнее движется шар. Чем больше столкновений испытает шар, тем менее интенсивным становится его движение.
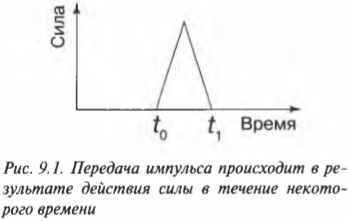
В повседневных ситуациях мы привыкли говорить, что тому или иному объекту или событию придают импульс. Рассмотрим процесс передачи импульса более подробно на примере бильярдного кия и шара. Процесс передачи импульса начинается в момент \( t_0 \) первого соприкосновения кия с шаром и заканчивается в момент \( t_1 \) утраты контакта между кием и шаром. В общем зависимость силы воздействия кия на шар от времени имеет сложный характер. Однако доя простоты можно положить, что она линейно возрастает от нулевого значения в момент \( t_0 \) первого соприкосновения, достигает максимального значения в момент наибольшего контакта, а потом снижается до нуля в момент \( t_1 \) утраты контакта между кием и шаром. Эта идеализированная зависимость силы взаимодействия кия и шара от времени графически показана на рис. 9.1.
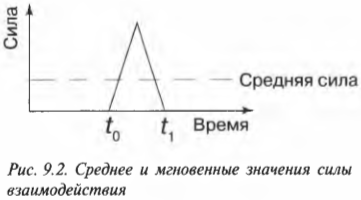
Время взаимодействия кия и шара очень мало (несколько долей секунды), и зафиксировать характер изменения силы можно только с помощью очень точного оборудования. Обычно физики используют не точные мгновенные значения, а усредненные величины. Например, в данном примере приобретенный шаром импульс \( \mathbf{p} \) равен произведению средней силы взаимодействия \( \mathbf{\overline{F}} \) и времени взаимодействия \( \Delta{t}=t_1-t_0 \):
Обратите внимание, что эта формула связывает векторы силы и импульса. Действительно, импульс — это вектор, обладающий некоторой величиной и направлением, совпадающим с направлением силы, например результирующей векторной суммы всех действующих на объект сил.
Из этой формулы ясно, что изменение импульса измеряется в системе СИ в ньютонах в секунду (Н·с), а в системе СГС — в динах-секундах (дин·с).
Получаем импульс
Изменение импульса (т.е. определенного количества движения) объекта означает изменение характера его движения. Причем это изменение зависит от массы и скорости объекта, поскольку импульс равен произведению скорости и массы объекта. Импульс является очень важной физической концепцией, которая используется не только в начальном курсе физики, но и в некоторых очень сложных разделах физики, например в физике элементарных частиц, где компоненты атомов носятся с огромными скоростями. Именно на основании анализа импульсов до и после столкновения элементарных частиц ученые могут делать выводы о поведении субатомного мира.
Общая идея импульса понятна даже тем, кому незнакомо это понятие. Не так уж легко остановить тележку, которая катится по склону горы. Дело в том, что тележка массивна и обладает большой скоростью. Еще труднее остановить огромный нефтяной танкер. Порой для полной остановки крупного танкера требуется около 30 км тормозного пути! И все это из-за огромного импульса, которым он обладает.
Чем больше масса движущегося объекта (представьте себе огромный танкер) и чем больше скорость объекта (представьте себе быстро плывущий танкер), тем больше импульс объекта.
Итак, импульс объекта равен:
Как видите, импульс — это вектор с определенной величиной и направлением (о векторах подробнее рассказывается в главе 4). Импульс, как и количество движения, измеряется в системе СИ в ньютонах в секунду (Н·с), а в системе СГС — в динах-секундах (дин·с).
Связываем работу силы и изменение импульса
Придать объекту импульс так же просто, как ударить клюшкой для гольфа по мячу. Достаточно применить элементарные алгебраические преобразования ко второму закону Ньютона и мы получим связь между работой силы и изменением импульса. С чего начать? Начнем со связи силы и скорости. Как известно, ускорение определяется следующей формулой:
где \( \Delta{v} \) — это изменение скорости за промежуток времени \( \Delta{t} \), \( v_0 \) — это начальная скорость в момент времени \( t_0 \), a \( v_1 \) — это конечная скорость в момент времени \( t_1 \). Теперь, если умножить обе части этой формулы на массу объекта \( m \), то слева получим:
Теперь, чтобы получить связь силы с импульсом объекта, умножим эту формулу на промежуток времени \( \Delta{t} \) и получим:
Посмотрите повнимательнее на правую часть формулы \( m(v_1-v_0) \). Поскольку импульс объекта с массой \( m \) равен \( p=mv \), то эта часть формулы выражает разницу конечного \( p_1=mv_1 \) и начального \( p_0=mv_0 \) импульса, т.е.:
Следовательно, в итоге получим:
Итак, справа имеем силу, умноженную на промежуток времени ее действия, т.е. \( F\Delta{t} \), а слева — изменение импульса \( \Delta{p} \). Убирая промежуточные выкладки, получим искомую формулу связи силы и изменения импульса объекта:
Произведение силы на время ее действия называется импульсом силы за то же время. (Его не следует путать с понятием импульс объекта \( p=mv \). Применение обоих этих понятий часто приводит к путанице, и потому понятие импульс силы используется довольно редко. — Примеч. ред.)
Пример: вычисляем импульс бильярдного шара
С помощью приведенных выше уравнений можно связать действующую на объект силу и приобретенный им импульс. Попробуем применить полученные знания при игре в бильярд. Допустим, что время контакта кия с бильярдным шаром приблизительно равно 5 мс (1 миллисекунда, или сокращенно 1 мс, равна 10-3 с). Насколько нужно изменить импульс неподвижного бильярдного шара, чтобы загнать его в лузу с отскоком от боковой стенки?
Пусть шар имеет массу 200 г (т.е. 0,2 кг). Допустим, что путем тщательных замеров и вычислений стало известно, что для попадания в лузу с отскоком от боковой стенки шару нужно приобрести скорость 20 м/с. Какую силу нужно приложить к кию для выполнения этой задачи?
Итак, в начальный момент времени шар покоится, т.е. начальная скорость \( v_0 \) = 0, а его конечная скорость \( v_1 \) должна быть равна 20 м/с. Вычислим необходимое изменение импульса по уже известной нам формуле:
Подставив значения получим:
Итак, необходимо изменить импульс шара на 4 кг·м/с. Вычислим, какую силу нужно для этого приложить за промежуток времени 5 мс по известной формуле:
откуда
Подставив значения, получим:
Итак, чтобы загнать бильярдный шар в лузу с отскоком от боковой стенки нужно прилагать к кию силу 800 Н в течение 5 мс.
Пример: определяем импульс капель дождя
После триумфальной демонстрации своих физических познаний в бильярдной попробуем использовать их в более привычной ситуации. Предположим, что на обратном пути домой внезапно начался дождь. Не беда, ведь под рукой есть зонт. Допустим, что на раскрытый зонт ежесекундно со средней скоростью около 10 м/с падает приблизительно 100 г капель воды. Вопрос: с какой силой нужно удерживать зонт массой 1 кг, чтобы удержать его под таким дождем?
Чтобы удержать зонт даже в отсутствие дождя, потребуется сила, равная весу зонта, то есть:
А как же подсчитать воздействие капель дождя? Предположим, что капли после падения на зонт почти мгновенно стекают по его почти горизонтальной поверхности. Даже в этом случае нам нужно учесть не только их массу, но и уменьшение скорости из-за встречи с зонтом. Действительно, летящие капли имеют начальную скорость 10 м/с, а после падения на зонт останавливаются, т.е. приобретают нулевую конечную скорость. Итак, имеем изменение импульса капель дождя, вызванное взаимодействием с зонтом. Попробуем оценить это изменение с помощью известной формулы:
Подставляя значения, получим:
Такое изменение импульса капель происходит ежесекундно. Свяжем теперь его с известной нам формулой:
Подставив значения, получим:
Итак, помимо силы 9,8 Н для удержания сухого зонта потребуется еще дополнительная сила 1 Н для компенсации торможения капель, т.е. всего потребуется сила 10,8 Н.
Наибольшую трудность при вычислениях изменения импульса под действием силы вызывает оценка времени действия этой силы. Поэтому при решении задач, связанных с изменением импульса, при столкновениях объектов обычно стремятся использовать другие параметры процесса, например скорость до и после столкновения, избегая оценок трудновычислимых параметров.
Изучаем закон сохранения импульса
Согласно этому закону, в изолированной системе без внешних сил общий импульс всех объектов системы до столкновений между ними равен общему импульсу всех объектов системы после столкновений между ними.
Если для анализа импульсов взаимодействующих объектов использовать приведенные выше формулировки с указанием силы и времени ее действия, то на это придется затратить чрезвычайно много усилий. Закон сохранения импульса позволяет избежать этих сложностей. Дело в том, что, применяя этот закон, можно полностью исключить из рассмотрения силы и время их действия.
Допустим, что два беспечных пилота космических кораблей А и Б не смогли избежать лобового столкновения своих машин. Во время столкновения корабль Б воздействовал на корабль А со средней силой \( F_{АБ} \). Согласно известной формуле о связи между силой и изменением импульса, получим для корабля А:
где \( m_{А} \) — это масса корабля A, \( v_{А1} \) — скорость корабля А после столкновения и \( v_{А0} \) — скорость корабля А до столкновения.
Аналогично, во время столкновения корабль А воздействовал на корабль Б со средней силой \( F_{БА} \). Опять по известной формуле о связи между силой и изменением импульса, получим для корабля Б:
где \( m_{Б} \) — это масса корабля Б, \( v_{Б1} \) — скорость корабля Б после столкновения и \( v_{Б0} \) — скорость корабля Б до столкновения.
Сложим оба последних равенства и получим следующее уравнение:
Опустим промежуточные выкладки и оставим только крайние левую и правую части этого равенства. Причем в правой части соберем отдельно члены начального и конечного состояний и получим:
Сумма \( m_Av_{A1}+m_Бv_{Б1} \) означает суммарный конечный импульс \( p_{1}=p_{A1}+p_{Б1} \) двух кораблей после столкновения, а сумма \( m_Av_{A0}+m_Бv_{Б0} \) — суммарный начальный импульс \( p_{0}=p_{A0}+p_{Б0} \) двух кораблей до столкновения. Следовательно, последнее уравнение можно переписать в следующем виде:
Если теперь ввести обозначение \( \sum\!{F} \) для суммы этих двух сил \( F_{АБ}+F_{БА} \), то получим:
При работе с изолированной, или замкнутой, системой объектов внешних сил нет. Именно такая ситуация рассматривается в данном примере.
Если два космических корабля столкнутся при отсутствии внешних сил, то согласно третьему закону Ньютона, \( F_{АБ}=-F_{БА} \). Иначе говоря, в замкнутой системе имеем:
А это означает, что:
Это равенство означает, что в изолированной системе без внешних сил начальный импульс двух сталкивающихся объектов до их столкновения равняется конечному импульсу после столкновения, что соответствует закону сохранения импульса.
Извлекаем тепло из суммарного импульса.
Всегда ли сохраняется суммарный импульс объектов при их лобовом столкновении и сцеплении? В реальном мире далеко не всегда. Дело в том, что часто при столкновениях объектов они необратимо деформируются и часть их кинетической энергии расходуется на необратимую деформацию и рассеивается в виде тепловой энергии. Однако для точного расчета такого преобразования кинетической энергии в тепловую требуется учесть много других сложных физических процессов. Эти процессы обычно не рассматриваются в начальном курсе физики, а тем более в этом курсе.
Измеряем скорость с помощью закона сохранения импульса
Попробуем применить закон сохранения импульса для расчета некоторых параметров движения. Предположим, что при игре в хоккей игрок А с массой 100 кг решил применить силовой прием против другого неподвижного игрока Б тоже с массой 100 кг (который оказался его братом-близнецом). Для этого игрок А разогнался до скорости 11 м/с, грубо толкнул игрока Б и, схватив его руками, устроил потасовку. С какой скоростью будут двигаться оба сцепившихся руками игрока после столкновения?
Будем считать, что в данном примере мы имеем дело с замкнутой системой (см. предыдущий раздел), поскольку мы пренебрегаем всеми внешними силами, включая силу трения. Хотя в вертикальном направлении на хоккеистов со стороны ледяного катка действует нормальная сила (подробнее о ней см. в главе 6), но она равна по величине весу игроков и противоположна по направлению и в сумме дает нуль.
Итак, рассмотрим горизонтальные проекции импульсов игроков. Согласно закону сохранения импульса, имеем:
Подставим в эту формулу массу и начальную скорость игроков (на самом деле нужно подставить массу \( m_А \) и начальную скорость \( v_{А0} \) только игрока А, поскольку игрок Б имел нулевую начальную скорость):
Конечный импульс \( p_1 \) должен быть равен произведению общей массы \( m_А+m_Б \) игроков на их конечную скорость \( v_{АБ1} \), т.е. получаем:
Из двух последних уравнений получаем:
откуда легко можно выразить конечную скорость \( v_{АБ1} \):
Подставляя значения, получим:
Конечная скорость двух игроков равна половине начальной скорости одного игрока. Этого следовало ожидать, ведь масса движущихся объектов увеличилась вдвое, а поскольку импульс сохраняется, то скорость должна уменьшиться во столько же раз.
Измеряем начальную скорость пули с помощью закона сохранения импульса
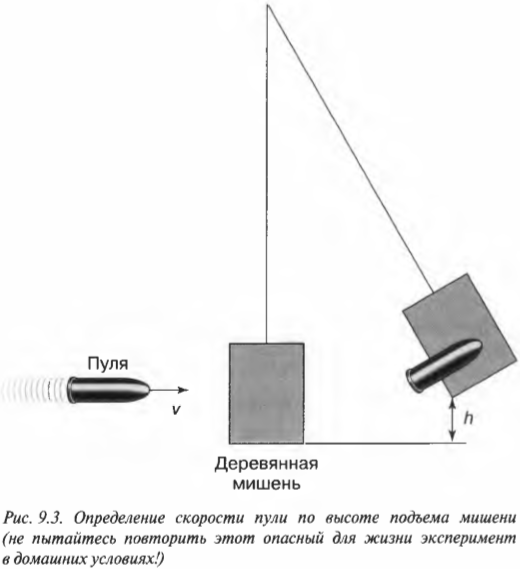
Закон сохранения импульса очень удобно использовать для определения скорости объекта, если ее нельзя или очень трудно измерить с помощью секундомера. Предположим, что изготовитель пуль хочет знать, какой будет начальная скорость новой пули. Как ему поступить? Для решения этой задачи ему предложили использовать приспособление, показанное на рис. 9.3.
Как оно может помочь? Оказывается, что если выстрелить пулей с массой \( m \) в массивную деревянную мишень с массой \( M \) и пуля застрянет в мишени, то, как и в примере с хоккеистами, конечная скорость мишени с пулей \( v_1 \) будет зависеть от начальной скорости пули \( v_0 \). Как именно? Для конкретного ответа на этот вопрос попробуем использовать закон сохранения импульса.
Итак, начальный суммарный импульс пули и мишени равен:
Поскольку пуля застряла в мишени, то конечный суммарный импульс пули и мишени равен:
Если пренебречь потерями энергии на преодоление трения при попадании пули в мишень, то согласно закону сохранения импульса, эти два импульса должны быть равны:
Тогда:
и искомая начальная скорость равна:
Итак, остается только определить конечную скорость \( v_1 \) мишени с застрявшей в ней пулей. Для этого нужно вспомнить закон сохранения энергии, который описывается в главе 8. Ведь после попадания пули мишень отклонится и поднимется на некоторую максимальную высоту \( h \), на которой ее скорость станет равной нулю. В этой точке ее кинетическая энергия \( \frac{(m+M)v^2_1}{2} \) преобразуется в потенциальную \( (m+M)gh \). Итак, согласно закону сохранения энергии получим:
Откуда легко вывести формулу для конечной скорости мишени с застрявшей в ней пулей \( v_1 \):
Подставим эту формулу в прежнее выражение для искомой начальной скорости пули:
и получим:
Пусть пуля имеет массу 50 г, деревянная мишень — 10 кг, а после попадания пули в нее мишень отклонилась и поднялась на максимальную высоту 0,5 м. Подставляя значения в приведенную выше формулу, получим:
Таким образом, мы определили начальную скорость пули. Изготовитель пуль будет просто в восторге от такого простого и удобного способа.
Упругие и неупругие столкновения
Изучение физики на примере столкновений разных тел — это очень интересное и увлекательное занятие. Во многом это объясняется тем, что многие вычисления значительно упрощаются благодаря закону сохранения импульса (более подробно он рассматривается в предыдущих разделах этой главы). Однако, как мы уже убедились в предыдущих примерах, в некоторых столкновениях одного этого закона недостаточно и нужно применять закон сохранения энергии. Это особенно полезно для анализа столкновений объектов со скоростями, векторы которых направлены не вдоль одной прямой (как в предыдущих примерах), а лежат в одной плоскости.
В реальной жизни такие ситуации происходят сплошь и рядом. Например, при изучении причин дорожно-транспортного происшествия часто требуется проанализировать начальные и конечные скорости столкнувшихся автомобилей. При сортировке вагонов нужно учитывать начальные и конечные скорости сталкивающихся вагонов и составов.
Что происходит в таких столкновениях, если столкнувшиеся объекты не “слипаются” друг с другом? Рассмотрим более общий пример: пусть два бильярдных шара сталкиваются дуг с другом с разными скоростями, направленными друг к другу под произвольным углом. Как определить их величину и направление их скоростей после столкновения? Для этого потребуется не только закон сохранения импульса, но и закон сохранения энергии.
Когда сталкивающиеся объекты отскакивают друг от друга: упругие столкновения
В реальном мире при столкновении тел всегда наблюдаются потери энергии на деформацию и рассеивание тепла. В некоторых случаях эти потери столь малы, что ими можно пренебречь, как, например, при столкновении двух бильярдных шаров. В физике такие столкновения с сохранением кинетической энергии сталкивающихся объектов называют упругими столкновениями. Итак, в упругом столкновении сохраняется общая кинетическая энергия замкнутой системы объектов, т.е. суммарная кинетическая энергия после столкновения равна суммарной кинетической энергии до столкновения.
Когда сталкивающиеся объекты не отскакивают друг от друга: неупругие столкновения
Если во время столкновения объектов какая-то часть энергии тратится на работу каких-то неконсервативных сил (например, на преодоление силы трения, деформацию и т.п.), то кинетическая энергия системы не сохраняется. Она частично преобразуется в другие формы энергии. Такие столкновения в физике называют неупругими столкновениями. Итак, в неупругом столкновении общая кинетическая энергия замкнутой системы объектов не сохраняется, т.е. суммарная кинетическая энергия после столкновения не равна суммарной кинетической энергии до столкновения. Примеры неупругих столкновений можно наблюдать в дорожно-транспортных происшествиях, когда столкнувшиеся машины деформируют друг друга или даже сцепляются и движутся как единое целое.
Совсем не обязательно, чтобы после неупругого столкновения объекты сцеплялись друг с другом. Достаточно, чтобы часть кинетической энергии “утрачивалась”, т.е. переходила в другую форму, например в тепловую энергию. Неупругое столкновение внешне может быть очень похоже на упругое столкновение, например при касательном столкновении двух машин с образованием легких повреждений. На образование этих повреждений необратимо тратится часть кинетической энергии, но машины могут независимо продолжить движение.
Упругие столкновение на прямой
Итак, мы уже выяснили, что при упругом столкновении кинетическая энергия сталкивающихся объектов сохраняется. Проще всего изучать особенности упругого столкновения, когда векторы скоростей находятся на одной прямой. Рассмотрим идеализированный пример столкновения двух машин с совершенно упругими (т.е. недеформирую- щимися) бамперами, которые движутся по прямой.
Упругое столкновение с более тяжелым объектом
Предположим, что вы решили прокатиться на автомобиле А с массой 300 кг и на скорости около 10 м/с столкнулись с внезапно остановившимся перед вами другим автомобилем Б с массой 400 кг. Какими будут скорости обоих автомобилей после их упругого столкновения?
Итак, до столкновения автомобиль А с массой \( m_А \) = 300 кг имел начальную скорость \( v_{А0} \) = 10 м/с, а автомобиль Б с массой \( m_Б \) = 400 кг — начальную скорость \( v_{Б0} \) = 0. Если считать систему двух автомобилей замкнутой, то их общий импульс должен сохраняться, то есть:
где \( v_{А1} \) — это конечная скорость автомобиля А после столкновения, a \( v_{Б1} \) — это конечная скорость автомобиля Б после столкновения.
У нас есть одно уравнение с двумя неизвестными \( v_{А1} \) и \( v_{Б1} \). Чтобы их найти, нужно иметь еще одно уравнение, связывающее эти неизвестные. Как насчет кинетической энергии? Действительно, поскольку столкновение было упругим, то кинетическая энергия объектов должна сохраняться, т.е. должно выполняться равенство:
Теперь у нас есть два уравнения и две неизвестных величины. С помощью простых алгебраических операций можно легко получить выражения для неизвестных скоростей \( v_{А1} \) и \( v_{Б1} \):
и
Подставляя значения в обе эти формулы, получим:
и
Анализируя полученные значения, можно легко восстановить ход событий. Итак, автомобиль А на скорости 10 м/с столкнулся с неподвижным автомобилем Б. После столкновения автомобиль А отскочил назад (об этом свидетельствует отрицательный знак конечной скорости \( v_{А1} \)) со скоростью 1,43 м/с, а автомобиль Б начал движение вперед со скоростью 8,57 м/с. Автомобиль А легче автомобиля Б, а что если бы было наоборот?
Упругое столкновение с более легким объектом
Предположим, что в предыдущем примере движущийся автомобиль А тяжелее неподвижного автомобиля Б. Пусть автомобиль А с массой 400 кг на скорости около 10 м/с сталкивается с внезапно остановившимся перед вами другим автомобилем Б с массой 300 кг. Вопрос остается прежним: какими будут скорости обоих автомобилей после их упругого столкновения?
Итак, до столкновения автомобиль А с массой \( m_А \) = 400 кг имеет начальную скорость \( v_{А0} \) = 10 м/с, а автомобиль Б с массой \( m_Б \) = 300 кг — начальную скорость \( v_{Б0} \) = 0. Используем уже известные нам формулы скоростей \( v_{А1} \) и \( v_{Б1} \):
и
Подставим в них новые значения и получим:
и
Как видите, более тяжелый движущийся автомобиль А после столкновения с более легким автомобилем Б смог продолжить движение в том же направлении, но с меньшей скоростью. Причем часть своего импульса он передал более легкому автомобилю Б.
Упругие столкновения в одной плоскости
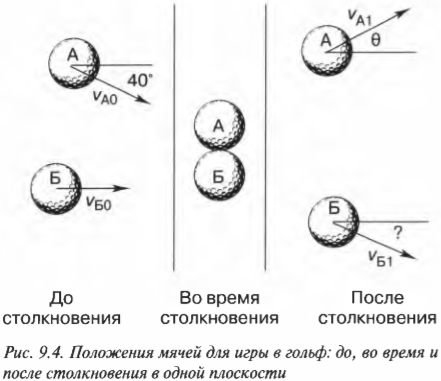
Столкновения объектов не всегда происходят по прямой линии. Например, бильярдные шары сталкиваются так, что векторы их скоростей могут быть направлены не вдоль одной прямой, а находится в одной плоскости под произвольным углом друг к другу. В этом случае нужно учитывать не только величину, но и направление скорости. Пусть во время игры в гольф два игрока одновременно (простим им это нарушение правил) ударяют по разным мячам А и Б, мячи упруго сталкиваются и продолжают движение, как показано на рис. 9.4. Какими будут скорости мячей после столкновения?
Попробуем решить эту задачу, учитывая, что мячи имеют одинаковую массу \( m \) = 46 г. Мяч А имеет начальную скорость \( v_{А0} \) = 1,0 м/с, а мяч Б — начальную скорость \( v_{Б0} \) = 2,0 м/с. Кроме того, пусть нам известны направления векторов начальных скоростей обоих мячей (см. рис. 9.4).
Для решения задачи нам потребуются закон сохранения импульса и закон сохранения энергии. Поскольку столкновение считается упругим, то кинетическая энергия системы сохраняется, т.е. согласно закону сохранения энергии, имеем:
или в более простой форме:
Если подставить вместо скоростей их компоненты по осям X и Y, то получим:
Так как трение здесь не учитывается, то в процессе столкновения внутренние силы упругого взаимодействия мячей направлены только по вертикальной оси Y. Эти силы не изменяют компоненты импульсов мячей по горизонтальной оси X:
и
Отсюда следует, что компоненты скоростей мячей по горизонтальной оси X после столкновения тоже не изменяются:
и
(То есть компоненты скоростей мячей по горизонтальной оси X в результате столкновения не изменились.)
Соотношение, полученное ранее из закона сохранения энергии:
с учетом постоянства компонент скоростей по оси X теперь будет иметь следующий вид:
или (поскольку \( v_{Б0у} \) = 0);
Согласно закону сохранения импульса, для компонент импульса по вертикальной оси Y имеем\( mv_{А1у}+mv_{Б1у}=mv_{А0у}+mv_{Б0у} \) или в более простой форме (поскольку \( v_{Б0у} \) = 0):
Из двух последних равенств нетрудно получить выражения для компонент скоростей по вертикальной оси Y:
и
Как видите, при таком упругом столкновении у мячей остались прежними их компоненты скоростей по горизонтальной оси X, и они “обменялись” компонентами скоростей по вертикальной оси Y. Это значит, что мяч А продолжит движение с нулевой компонентой \( v_{А1у} \), т.е. по горизонтали, а мяч Б продолжит движение под углом \( \alpha \), который легко вычислить по формуле:
где знак “минус” перед значением угла означает, что на рис. 9.4 угол откладывается в направлении против часовой стрелки.
А скорости мячей после столкновения будут равны
и:
Подставив значения, получим:
и






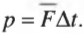
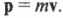
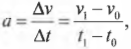
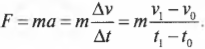
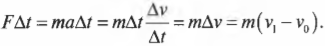
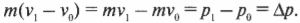
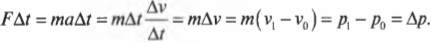
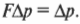
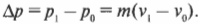
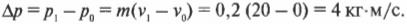
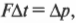
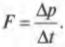
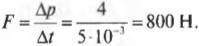
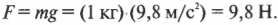
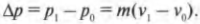
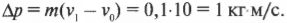
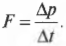
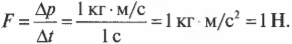
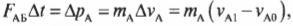
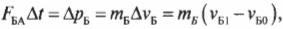
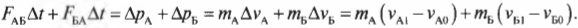
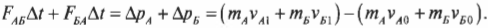
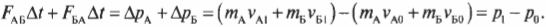
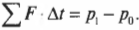
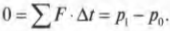

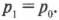
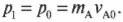
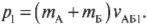
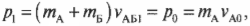
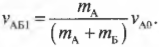
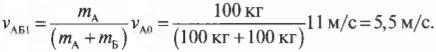
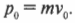
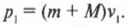
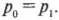
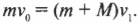
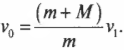
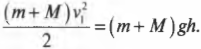
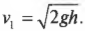
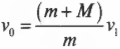
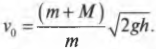
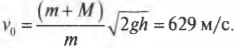
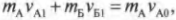
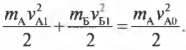
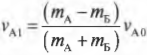
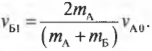
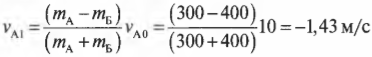
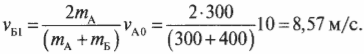
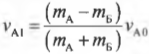
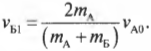
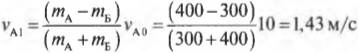
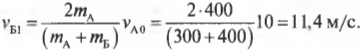
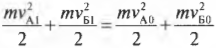
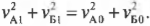
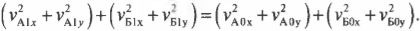
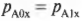
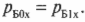
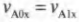
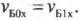
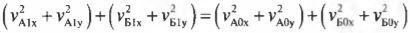
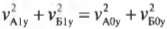
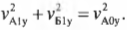
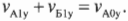
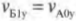
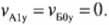
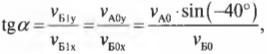
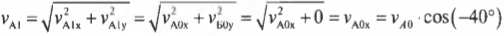
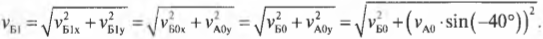
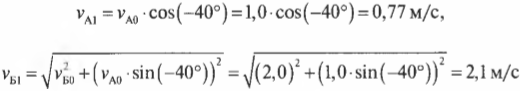
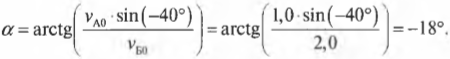
Добавить комментарий