Глава 7. Движемся по орбитам

В этой главе. . .
- Постигаем равномерное вращательное движение
- Изучаем угловое ускорение
- Испытываем влияние центростремительной силы
- Учитываем перемещение, скорость и ускорение
- Движемся по орбите под действием законов Ньютона и силы гравитационного притяжения
- Поддерживаем вращение в вертикальной плоскости
Вращательное движение выполняют искусственные спутники вокруг планет, гоночные автомобили по трекам и даже пчелы вокруг ульев. В предыдущих разделах рассматривались такие характеристики прямолинейного движения, как перемещение, скорость и ускорение. В этой главе мы снова рассмотрим их, но теперь уже для вращательного движения.
Для перечисленных выше характеристик прямолинейного движения есть аналоги, характеризующие вращательное движение, а именно: угловое перемещение, угловая скорость и угловое ускорение. Как видно из их названия, роль перемещения во вращательном движении играет угол. Угловая скорость обозначает величину угла поворота за единицу времени, а угловое ускорение — изменение угловой скорости за единицу времени. Все, что нужно сделать, чтобы освоить премудрости вращательного движения, это взять уравнения прямолинейного движения и заменить в них одни характеристики другими: перемещение поменять на угол, скорость — на угловую скорость и ускорение — на угловое ускорение.
Содержание
- Держим курс: равномерное вращательное движение
- Меняем направление: центростремительное ускорение
- Стремимся к центру: центростремительная сила
- Вписываемся в повороты: учитываем радиус и наклон
- Вращательное движение: перемещение, скорость и ускорение
- Бросаем яблоко: закон всемирного тяготения Ньютона
- Вращаемся вдоль вертикальной плоскости
Держим курс: равномерное вращательное движение
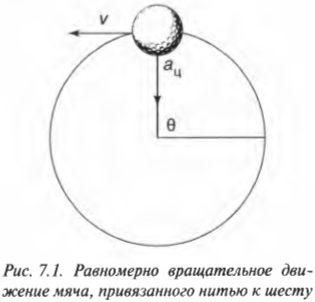
Если объект движется с постоянной по величине скоростью по окружности, то такое движение называется равномерным вращательным движением. Примерами такого движения являются движение гоночного автомобиля по круглому треку и стрелки на циферблате часов. На рис. 7.1 показан мяч для игры в гольф, привязанный нитью к шесту и совершающий движение по окружности. Мяч совершает движение с одинаковой по величине скоростью, но с изменяющимся направлением. Потому такое движение мяча называется равномерным вращательным движением.
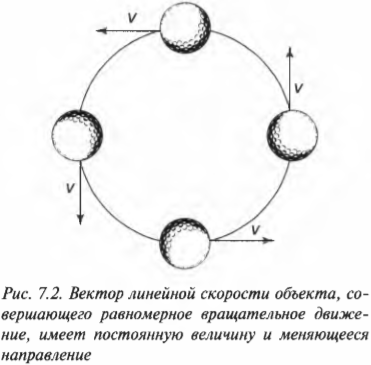
Время, которое требуется мячику (или какому-либо другому объекту), чтобы полностью обогнуть окружность, называется периодом и обозначается символом \( T \). Период и линейную скорость можно легко связать, если известно пройденное расстояние, т.е. длина окружности \( 2\pi r \), а точнее ее радиус \( r \). Итак, линейная скорость мячика \( v \) равна:
а период вращения \( T \) равен:
Допустим, что длина нити равна 1 м, а период вращения равен 0,5 с. Чему в таком случае будет равна линейная скорость мячика? Подставим численные значения в одно из предыдущих соотношений и получим:
Итак, мячик вращается с линейной скоростью 13 м/с!
Меняем направление: центростремительное ускорение
При вращательном движении по окружности линейная скорость мячика постоянно меняет направление, как показано на рис. 7.2. Ускорение, характеризующее такое изменение скорости, называется центростремительным (или центробежным). В любой точке вращательного движения с постоянной величиной и меняющимся направлением вектор линейной скорости перпендикулярен радиусу.
Это правило справедливо для всех объектов: вектор линейной скорости объекта, равномерно вращающегося по окружности, всегда перпендикулярен радиусу окружности.
Если в показанных на рис. 7.2 положениях нить, удерживающая мяч, оборвется, то куда полетит мяч? Если в этот момент вектор линейной скорости направлен влево, то мяч полетит влево, а если этот вектор направлен вправо, то мяч полетит вправо, и т.д. Этот, казалось бы, простой и интуитивно понятный момент часто вызывает трудности у тех, кто впервые постигает физику.
Всегда следует помнить, что вектор линейной скорости объекта, выполняющего равномерное вращательное движение, всегда направлен под прямым углом к радиусу вращения в текущей точке траектории. (В общем случае неравномерного криволинейного движения эта компонента вектора скорости, перпендикулярная радиусу вращения и касательная к траектории движения, называется тангенциальной компонентой, а перпендикулярная ей компонента — нормальной компонентой. — Примеч. ред.)
Управляем скоростью с помощью центростремительного ускорения
Особенностью равномерного вращательного движения является постоянство величины линейной скорости. Это значит, что вектор ускорения не имеет компоненты, параллельной вектору линейной скорости, поскольку в противном случае величина линейной скорости менялась бы. Однако при равномерном вращательном движении меняется только направление линейной скорости. Такое изменение линейной скорости поддерживается центростремительным ускорением, направленным к центру окружности вращения и перпендикулярно вектору линейной скорости.
В примерах на рис. 7.1 и 7.2 на мяч со стороны нити действует сила натяжения нити, которая поддерживает его движение по окружности. Именно эта сила сообщает мячу центростремительное ускорение \( a_ц \), вектор которого показан на рис. 7.1. (Попробуйте раскрутить мяч с помощью привязанной к нему нити, и вы сразу же почувствуете действие этой силы со стороны нити.)
Часто возникает вопрос: если вектор ускорения мяча направлен к центру окружности, то почему мяч не движется к центру? Дело в том, что при равномерном вращательном движении это ускорение меняет только направление, а не величину линейной скорости.
Определяем величину центростремительного ускорения
Нам уже известно направление вектора центростремительного ускорения, а чему же равна его величина? Итак, величина центростремительного ускорения объекта, равномерно движущегося с линейной скоростью \( v \) по окружности с радиусом \( r \), равна:
Как видите, величина центростремительного ускорения обратно пропорциональна радиусу окружности \( r \) и прямо пропорциональна квадрату скорости \( v \). Поэтому не удивительно, что автомобиль на более крутых поворотах испытывает более сильное центростремительное ускорение.
Стремимся к центру: центростремительная сила
На крутых поворотах действие центростремительного ускорения обеспечивается трением шин по дороге. Какую силу нужно приложить, чтобы удержать движущийся со скоростью \( v \) автомобиль на повороте с радиусом кривизны \( r \)?
Допустим, что в примере на рис. 7.1 легкий мяч заменили на тяжелое пушечное ядро. Теперь, чтобы поддерживать движение ядра по окружности с тем же радиусом и периодом вращения, потребуется гораздо большая сила.
Дело в том, что сила \( F=ma \) равна произведению ускорения \( a \) и массы \( m \), а значит, увеличение массы объекта (замена мяча на ядро) неизбежно приводит к необходимости увеличения силы для обеспечения прежнего ускорения.
Центростремительная сила \( F_ц \), необходимая для равномерного вращения по окружности с радиусом \( r \) объекта массой \( m \) с постоянной скоростью \( v \), равна:
С помощью этого уравнения можно легко определить силу, необходимую для равномерного вращения объекта по окружности с известной массой, скоростью и радиусом окружности.
Обратите внимание, что если объект движется по той же окружности, но с разной скоростью, то он будет испытывать разную центростремительную силу.
В примерах на рис. 7.1 и 7.2 мяч движется со скоростью \( v \) = 13 м/с и удерживается нитью длиной 1,0 м, т.е. в данном случае радиус окружности \( r \) = 1 м. Какая сила потребуется, чтобы поддерживать такое же движение для пушечного ядра с массой 10 кг? Подставляя численные значения в уже известную нам формулу, получим:
Приличная сила! Остается только надеяться, что ваши руки достаточно сильны, чтобы удержать ядро.
Является ли центростремительная сила реальной силой?
Центростремительная сила не является каким-то особым типом взаимодействия. Она имеет отношение только к объекту, движущемуся по криволинейной траектории, и необходима для удержания объекта на данной траектории. Поэтому ее часто называют центростремительно-необходимой силой. Довольно часто новички считают центростремительную силу каким-то новым фундаментальным типом взаимодействия. И это понятно, поскольку известные нам силы (например, сила гравитации и сила трения) имеют вполне определенный источник, который не зависит от траектории движения. Но это совсем не так для центростремительной силы. Центростремительная сила возникает из необходимости удержания объекта на криволинейной траектории. Сумма всех остальных сил, действующих на объект, который движется по криволинейной траектории, должна быть равна центростремительной силе. (Если объект движется по прямолинейной траектории, а затем ему нужно изменить направление движения, то для этого придется приложить силу, равную центростремительной силе. — Примеч. ред.)
Вписываемся в повороты: учитываем радиус и наклон
Если вам приходилось ехать на автомобиле или велосипеде или даже бежать трусцой, то наверняка вы заметили, что в крутой поворот проще вписаться, если поверхность дороги немного наклонена внутрь поворота. Из опыта известно, что чем больше наклон, тем проще вписаться в поворот. Это объясняется тем, что в таком случае на вас действует меньшая центростремительная сила. Центростремительная сила обеспечивается силой трения о поверхность дороги. Если поверхность дороги покрыта льдом, то сила трения становится меньше и потому часто не удается вписаться в поворот на обледеневшей дороге на большой скорости.
Представьте, что автомобилю с массой 1000 кг нужно вписаться в поворот с радиусом Юм, а коэффициент трения покоя (подробнее о нем см. главу6) равен 0,8. (Здесь используется коэффициент трения покоя, поскольку предполагается, что шины по поверхности дороги.) Какую максимальную скорость может развить этот автомобиль без риска не вписаться в поворот. Итак, сила трения покоя шин о поверхность дороги \( F_{трение\,покоя} \) должна обеспечивать центростремительную силу:
где \( m \) — это масса автомобиля, \( v \) — его скорость, \( r \) — радиус, \( \mu_п \) — коэффициент трения покоя, a \( g \) = 9,8 м/с2 — ускорение свободного падения под действием силы гравитации. Отсюда легко находим скорость:
(Обратите внимание, что максимальная безопасная скорость прохождения поворота не зависит от массы автомобиля. — Примеч. ред.)
Это выражение выглядит очень просто, а после подстановки в него численных значений получим:
Итак, максимальная скорость безопасного проезда при таком повороте равна 8,9 м/с. Пересчитаем в единицы “км/ч”, в которых скорость указана на спидометре, и сравним. Получается, что 8,9 м/с = 32 км/ч, а на спидометре всего 29 км/ч. Прекрасно, но далеко не все водители умеют так быстро рассчитывать безопасную скорость прохождения поворотов. Поэтому конструкторы дорог часто строят повороты с наклоном внутрь, чтобы обеспечить центростремительное ускорение не только за счет силы трения, но и за счет горизонтальной компоненты силы гравитации.
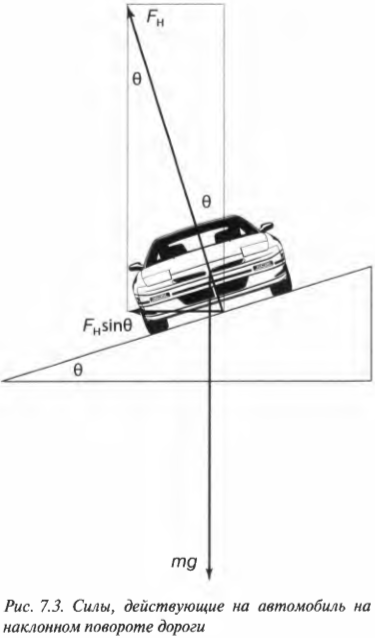
На рис. 7.3 показан пример поворота дороги с некоторым наклоном под углом \( \theta \) к горизонтали. Предположим, что конструкторы решили полностью обеспечить центростремительное ускорение только за счет горизонтальной компоненты силы гравитации (т.е. без учета силы трения) \( F_н\sin\theta \), где \( F_н \) — это нормальная сила (подробнее о ней см. в главе 6). Тогда:
В вертикальном направлении на автомобиль действует сила гравитации \( mg \), которая уравновешивается вертикальной компонентой нормальной силы \( F_н\cos\theta \):
или, иначе выражая это соотношение, получим:
Подставляя это выражение в прежнее соотношение между центростремительной силой и нормальной силой, получим:
Поскольку \( \sin\theta/\!\cos\theta=tg\,\theta \) в то
Отсюда легко получаем, что угол наклона поворота дороги \( \theta \) равен:
Именно это уравнение используют инженеры при проектировании дорог. Обратите внимание, что масса автомобиля не влияет на величину угла, при котором центростремительная сила полностью обеспечивается только горизонтальной компонентой нормальной силы. Попробуем теперь определить величину угла наклона поворота с радиусом 200 м для автомобиля, движущегося со скоростью 100 км/ч или 27,8 м/с:
Для обеспечения безопасного движения автомобиля со скоростью 100 км/ч в повороте с радиусом 200 м без учета силы трения, инженеры должны создать наклон около 22°. Отлично, из вас может получиться неплохой инженер-конструктор автомагистралей!
Вращательное движение: перемещение, скорость и ускорение
Если вы привыкли решать задачи о прямолинейном движении типа “некто движется из пункта А в пункт Б”, то задачи о вращательном движении можно формулировать аналогично, но для этого нужно приобрести некоторый опыт. На рис. 7.1 мяч движется криволинейно по окружности, а не прямолинейно по линии. Это движение можно было бы описать как комбинацию прямолинейных движений с координатами X и Y. Однако гораздо удобнее характеризовать его иначе, а именно как вращательное движение с одной координатой \( \theta \). В данном примере вращательного движения перемещение можно характеризовать углом \( \theta \) так же, как в прямолинейном движении перемещение характеризуется расстоянием \( s \). (Более подробно перемещение при прямолинейном движении описывается в главе 3.)
Стандартной единицей измерения перемещения при вращательном движении является радиан (рад), а не градус. Полная окружность охватывает угол величиной \( 2\pi \) радиан, что равно 360°. Соответственно, половина окружности охватывает угол величиной \( \pi \) радиан, а четверть окружности — \( \pi/2 \).
Как преобразуются величины углов из градусов в радианы и обратно? Достаточно определить, сколько радиан приходится на один градус, т.е. вычислить отношение \( 2\pi \)/360°. Например, величина угла 45° в радианах равна:
Аналогично, для преобразования величины угла из радианов в градусы следует определить, сколько градусов приходится на один радиан, т.е. вычислить отношение 360°/\( 2\pi \). Например, величина угла \( \pi/2 \) в градусах равна:
Формулировка вращательного движения в терминах прямолинейного движения очень удобна. Напомним основные формулы прямолинейного движения, которые подробно описываются в главе 3:
Теперь для вывода аналогичных основных формул вращательного движения достаточно в формулах прямолинейного движения вместо расстояния \( s \), которое характеризует прямолинейное перемещение, подставить угол \( \theta \), который характеризует угловое перемещение. А как определяется угловая скорость? Очень просто. Угловая скорость \( \omega \) определяется аналогично, как изменение угла за единицу времени, и равна количеству радианов, пройденных за секунду:
Обратите внимание, как похоже это выражение для угловой скорости на выражение для линейной скорости:
Давайте теперь вычислим угловую скорость мяча на рис. 7.1. Он совершает полный круг, охватывающий \( 2\pi \) радиан, за 1/2 с, а значит, его угловая скорость равна:
(Величина угла, выраженная в радианах, равна отношению длины дуги окружности к длине ее радиуса. Поэтому радиан — это безразмерная величина, и ее обозначение (рад) часто опускается. Соответственно, угловую скорость принято указывать “в обратных секундах” как с-1, т.е. без указания единицы измерения углов. — Примеч. ред.)
Угловое ускорение \( \alpha \) определяется аналогично линейному ускорению:
Оно определяется как изменение угловой скорости за единицу времени и измеряется в радианах на секунду в квадрате. Если скорость за 2 с изменилась от величины \( 4\pi c^{-1} \) до величины \( 8\pi c^{-1} \), то чему равно угловое ускорение? Подставим эти численные значения в предыдущую формулу и получим:
Итак, для описания вращательного движения у нас есть следующие аналоги: для линейного перемещения \( s \) — угловое перемещение \( \theta \), для линейной скорости \( v \) — угловая скорость \( \omega \) и для линейного ускорения \( a \) — угловое ускорение \( \alpha \).
На основании этой аналогии можно легко вывести основные формулы вращательного движения (подобно основным формулам прямолинейного движения, которые подробно описываются в главе 3):
Более подробно эти выражения рассматриваются далее в главе 10 при описании момента импульса и момента силы.
Бросаем яблоко: закон всемирного тяготения Ньютона
Чтобы проводить опыты с вращательным движением, необязательно привязывать мячики к нитям и вращать их вокруг себя. Например, Луне совсем не нужны никакие нити, чтобы вращаться вокруг Земли. А дело в том, что необходимую центростремительную силу, вместо силы натяжения нити, обеспечивает сила гравитационного притяжения.
Один из важнейших законов физики, а именно закон всемирного тяготения, вывел еще сэр Исаак Ньютон. Согласно этому закону любые два тела притягиваются друг к другу с некоторой силой. Величина этой силы притяжения между телами с массами \( m_1 \) и \( m_2 \), которые находятся на расстоянии \( r \) друг от друга, равна:
где \( G \) — это константа, равная 6,67·10-11 Н·м2/кг2.
Благодаря этому уравнению можно легко вычислить силу гравитационного притяжения между двумя телами. Например, какова сила гравитационного притяжения между Землей и Солнцем? Солнце имеет массу около 1,99·1030 кг, Земля — 5,97·1024 кг, а расстояние между ними равно 1,50·1011 м. Подставляя эти числа в закон всемирного тяготения Ньютона, получим:
Историческая яблоня
Как известно, яблоко упало на голову Исаака Ньютона, и он открыл закон всемирного тяготения. Неужели это так и было? Правда ли, что какое-то падающее яблоко натолкнуло его на верную мысль или, по крайней мере, привлекло внимание Ньютона к данной теме? Согласно последним историческим исследованиям, весьма маловероятно, что именно падение яблока на голову великого ученого вдохновило его. Скорее всего, глядя в окно на падающие яблоки в саду, он нашел еще один пример всемирного тяготения. Историки до сих пор спорят, какое именно дерево является “яблоней Ньютона”. Сотрудники поместья матери Ньютона в Вулсторпе возле Грантхэма в Линкольншире (Великобритания) утверждают, в ее семейном саду до сих пор сохранились потомки “яблони Ньютона”.
Возвращаясь с небес на грешную землю, давайте вычислим силу притяжения между двумя влюбленными на парковой скамейке. Какой величины может быть сила гравитационного притяжения между ними, если, едва встретившись, они обнимают друг друга все сильнее и сильнее? Допустим, что они весят по 75 кг и находятся на расстоянии не больше полуметра. Подставляя эти значения в уже известную нам формулу, получим:
Ничтожная сила в несколько миллионных долей ньютона!
Вычисляем силу гравитационного притяжения на поверхности Земли
Описанное выше уравнение \( F=(Gm_1m_2)/r^2 \) для силы гравитационного притяжения справедливо независимо от расстояния между двумя массивными телами. В обыденных ситуациях часто приходится иметь дело с небольшими (по сравнению с размерами Земли) объектами на поверхности Земли, т.е. на фиксированном расстоянии между центром Земли и центром небольшого объекта. Силу гравитационного притяжения (или силу тяжести), действующую на небольшой объект, часто называют весом. Вес \( F_g \) равен произведению массы \( m \) на ускорение свободного падения \( g \), т.е. \( F_g = mg \). Массу измеряют в граммах, килограммах, центнерах, каратах и т.д., а вес — в динах, ньютонах и даже фунт-силах.
Попробуем вычислить ускорение свободного падения на поверхности Земли, пользуясь законом всемирного тяготения. Формула веса тела с массой \( m_1 \) нам известна:
Она создается силой гравитационного притяжения между этим телом и Землей и равна этой силе:
Здесь \( r \) — это радиус Земли, равный 6,38·106 м, а \( m_2 \) — ее масса, равная 5,97·1024 кг.
Сокращая массу тела \( m_1 \) в обеих половинах предыдущего равенства, получим:
Подставляя численные значения, получим:
Так, благодаря закону всемирного тяготения Ньютона мы смогли вычислить значение ускорения свободного падения, уже известное нам из прежних глав. Как видите, для этого нам потребовались значения константы всемирного тяготения \( G \), радиуса Земли \( r \) и ее массы \( m_2 \). (Конечно, значение ускорения свободного падения \( g \) можно определить экспериментально, измеряя время падения предмета с известной высоты. Но, согласитесь, гораздо интересней использовать последнюю формулу, для применения которой потребуется экспериментально измерить… радиус и массу Земли. Шутка!)
Исследуем орбитальное движение с помощью закона всемирного тяготения
Небесные тела в космическом пространстве из-за силы гравитационного притяжения вращаются друг относительно друга: спутники — вокруг своих планет (как Луна — вокруг Земли), планеты — вокруг звезд (как Земля — вокруг Солнца в Солнечной системе), а звезды — вокруг центра Галактики (как Солнце — вокруг центра нашей галактики, т.е. Млечного пути), а Галактика — вокруг местной группы галактик (как Млечный путь — вокруг нашей Местной группы галактик). Во всех этих случаях тела удерживаются центростремительной силой, которую обеспечивает сила гравитации. Как показано ниже, такая центростремительная сила несколько отличается от той, которая известна нам по прежнему примеру с вращающимся на нитке мячом для игры в гольф. В следующих разделах рассматриваются широко известные законы вращения тел под действием силы гравитационного притяжения, так называемые законы Кеплера, т.е. соотношения между параметрами вращательного движения: периодами вращения, радиусами и площадями орбит вращения.
Вычисляем скорость спутника
Чему равна скорость спутника, вращающегося вокруг планеты по орбите с постоянным радиусом? Ее можно легко определить, приравнивая центростремительную силу:
и силу гравитации:
В итоге получаем:
После простых алгебраических операций получим следующее выражение для скорости вращения:
Это уравнение определяет скорость вращения спутника по постоянной орбите независимо от его происхождения, будь-то искусственный спутник Земли, как рукотворный космический корабль на постоянной орбите, или естественный спутник Земли, как Луна.
Подсчитаем скорость вращения искусственного спутника Земли, вращающегося вокруг Земли. Для этого нужно в предыдущую формулу подставить массу Земли и расстояние от космического орбитального спутника до центра Земли.
Рукотворные спутники Земли обычно вращаются на высоте около 640 км, а радиус Земли, как известно, равен 6,38·106 м. Можно считать, что искусственные спутники вращаются на круговой орбите с радиусом около 7,02·106 м. Подставляя это и другие известные нам численные значения в предыдущую формулу, получим:
В этом месте нужно сделать несколько важных замечаний.
Значение 7,02·106 м в знаменателе обозначает расстояние от спутника до центра Земли, а не расстояние от спутника до поверхности Земли, равное 640 км. Помните, что в законе всемирного тяготения под расстоянием между телами подразумевается расстояние между их центрами масс, а не между их поверхностями.
В данном примере предполагается, что космический корабль находится достаточно высоко и не испытывает влияние атмосферы, например силу трения от соприкосновения с ней. На самом деле это не так. Даже на такой большой высоте как 640 км, космический корабль теряет скорость, вследствие трения в разреженных слоях атмосферы. В результате его скорость уменьшается, а сам корабль постепенно снижается. (Более подробно об этом рассказывается ниже.)
Движение искусственного спутника вокруг Земли можно рассматривать как “вечное” падение. От фактического падения его “удерживает” только то, что вектор скорости всегда направлен перпендикулярно радиусу окружности вращения. Действительно, именно из-за такого “вечного” падения космонавты испытывают чувство невесомости. Дело в том, что космонавты и их космический корабль “вечно” падают по касательной к орбите вращения вокруг Земли, но при этом нисколько не приближаются к Земле.
В практических целях часто важнее знать период обращения искусственного спутника, а не его скорость. Это нужно, например, в ситуации, когда требуется определить момент выхода на связь с космическим кораблем.
Вычисляем период обращения спутника
Периодом обращения спутника называется время, которое необходимо ему, чтобы совершить полный цикл вращательного движения по орбите. Если нам известна орбитальная скорость движения \( v \) спутника по окружности с радиусом \( r \) (см. предыдущий раздел), то можно легко и просто вычислить период обращения \( T \). За период обращения спутник преодолевает расстояние, равное длине окружности \( 2\pi r \). Это значит, что орбитальная скорость \( v \) спутника равна \( 2\pi r/T \). Приравнивая это соотношение и полученное ранее выражение для орбитальной скорости
где \( m \) — масса Земли, получим:
Отсюда легко получить следующее выражение для периода обращения спутника:
А на какой высоте должен находиться спутник, чтобы вращаться с периодом обращения Земли вокруг своей оси, равным 24 часам или 86400 с? Это вовсе не праздный вопрос. Такие спутники действительно существуют и используются для обеспечения непрерывной связи в данном регионе. Действительно, ведь, обращаясь вокруг Земли с тем же периодом, что и Земля, спутник на такой геостационарной орбите постоянно находится над одной и той же точкой поверхности Земли. Несколько таких спутников образуют систему глобального позиционирования. Итак, с помощью предыдущей формулы вычислим радиус окружности вращения спутника на стационарной орбите:
Подставляя численные значения, получим:
Отнимая от этой величины 4,23·107 м, значение радиуса Земли, равное 6,38·106 м, получим приблизительно 3,59·107 м, т.е. около 35900 км. Именно на таком расстоянии от Земли вращаются спутники глобальной системы позиционирования.
На практике спутники на геостационарной орбите все же теряют скорость из- за взаимодействия с магнитным полем Земли (подробнее о магнитном поле рассказывается в следующих главах). Поэтому спутники оборудованы небольшими двигателями для корректировки их положения на геостационарной орбите.
Вращаемся вдоль вертикальной плоскости
Наверняка вам приходилось наблюдать, как отважные мотоциклисты, велосипедисты или скейтбордисты вращаются внутри круглого трека, расположенного в вертикальной плоскости. Почему сила тяжести не опрокидывает их в самой верхней точке, где они находятся вверх ногами? Как быстро им нужно двигаться, чтобы сила гравитации не превышала центростремительной силы?
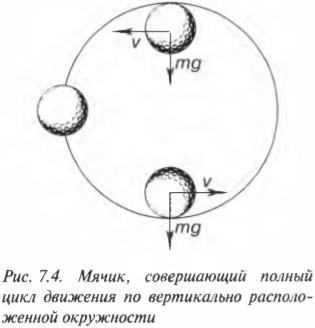
Рассмотрим эту ситуацию подробнее с помощью схемы на рис. 7.4. Для простоты предположим, что вместо отважных спортсменов маленький мячик совершает движение по окружности, расположенной в вертикальной плоскости. Итак, предыдущий вопрос формулируется следующим образом: “Какой минимальной скоростью должен обладать мячик, чтобы совершить полный цикл движения по вертикально расположенной окружности?”. Какому основному условию должно отвечать движение мячика, чтобы он совершил полный цикл движения по такой окружности и не упал в самой верхней точке?
Для прохождения самой верхней точки без падения мячик должен обладать минимальной скоростью, достаточной для создания такой центростремительной силы, которая была бы не меньше силы гравитации.
При таких условиях нормальная сила со стороны трека будет равна нулю, а единственной силой, которая будет удерживать объект на окружности, является сила гравитации. Поскольку центростремительная сила равна:
а сила гравитации равна:
то, приравнивая их, получим:
Отсюда получим выражение для минимально необходимой скорости для безопасного движения по окружности, расположенной в вертикальной плоскости:
Обратите внимание, что на величину минимально необходимой скорости для безопасного движения объекта по окружности, расположенной в вертикальной плоскости, не влияет масса объекта, будь-то мячик, мотоцикл или гоночный автомобиль.
Любой объект, движущийся с меньшей скоростью, в самой верхней точке трека неизбежно отклонится от траектории движения по окружности и упадет. Давайте вычислим величину минимально необходимой скорости для безопасного движения по окружности с радиусом 20 м. Подставляя численные значения в предыдущую формулу, получим:
Итак, для безопасного движения по окружности с радиусом 20 м объект (мячик, мотоцикл или гоночный автомобиль) должен иметь скорость не менее 14 м/с, т.е. около 50 км/ч.
Учтите, что для безопасного движения по окружности такую минимальную скорость объект должен иметь в самой верхней точке! Для того чтобы развить такую скорость в верхней точке, объекту в нижней точке нужно иметь гораздо большую скорость. Действительно, ведь чтобы добраться до верхней точки объекту придется какое-то время преодолевать силу гравитации с неизбежной потерей скорости.
Возникает вопрос: какую минимальную скорость в нижней точке должен иметь объект для безопасного движения по такой окружности? Подробный ответ на этот вопрос будет дан в части III этой книги, в которой рассматриваются такие понятия, как “кинетическая энергия”, “потенциальная энергия” и “преобразование энергии из одной формы в другую”.






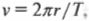
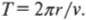

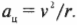
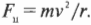
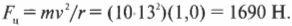
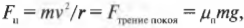
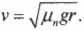
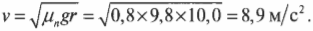
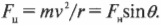
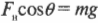
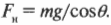
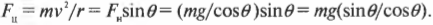
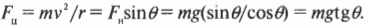
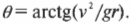
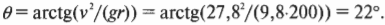
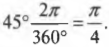
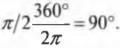
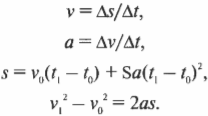
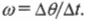
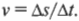
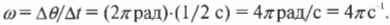
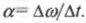
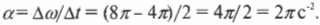
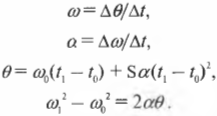
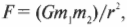
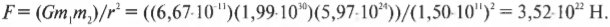
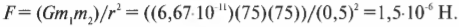
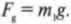
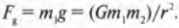
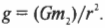
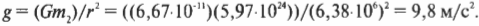
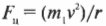
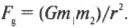

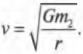
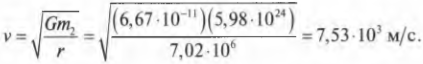
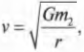
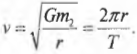
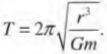
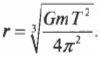
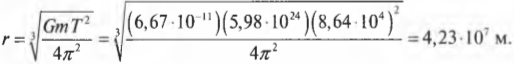
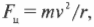
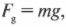
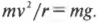
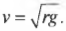
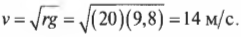
Добавить комментарий
[…] Источник […]
[…] Источник […]
[…] Источник […]
[…] Источник […]
[…] Источник […]
[…] Источник […]
движение- равномерное откуда в нём центростремительное ускорение
Притяжение земли действует не по инерции, а по природе поля притяжения.
При равномерном вращательном движении меняется скорость, а именно, — её направление. Ускорение, как известно, — это изменение скорости. Центростремительное ускорение вызывается изменением направления скорости.