Глава 20. Немного света на зеркала и линзы

В этой главе…
- Знакомимся с основами оптики
- Наблюдаем за искривлением света
- Изучаем поведение плоских, вогнутых и выпуклых зеркал
- Смотрим сквозь собирающие и рассеивающие линзы
Эта глава “просветит” читателя, т.е. в ней он познакомится с основами оптики и узнает о том, что происходит со светом в различных условиях и при прохождении разных материалов. Свет искривляется при прохождении границы между воздухом и водой, что можно легко заметить на рыбалке. При прохождении линзы свет либо собирается (что можно заметить при поджигании бумаги с помощью солнечных лучей), либо рассеивается (как в очках для близоруких людей). Здесь также описывается поведение света при отражении от зеркал.
Содержание
Все о зеркалах
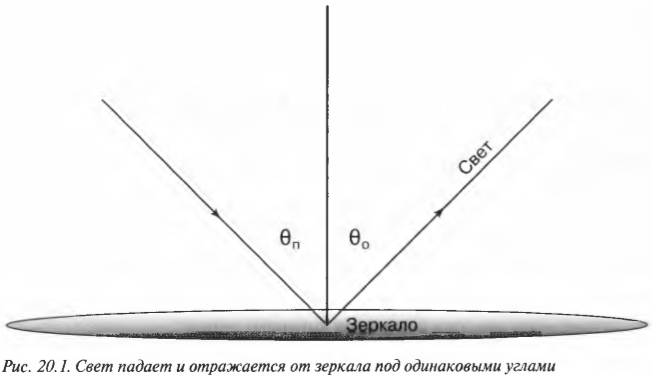
Как известно, свет отражается от зеркал, и законы физики могут многое сказать о том, как это происходит. Рассмотрим типичный случай, показанный на рис. 20.1. Свет падает на зеркало слева и отражается от зеркала вправо. Как видите, свет падает на зеркало под определенным углом к нормали (нормаль — это прямая, проведенная перпендикулярно к поверхности зеркала). Такой угол между линией падения и нормалью называется углом падения и обозначается \( \theta_п \). А угол, под которым свет отражается (т.е. между линией отражения и нормалью), называется углом отражения и обозначается \( \theta_о \).
Согласно закону отражения, угол падения равен углу отражения: \( \theta_п=\theta_о \).
Иначе говоря, если свет падает на зеркало под углом 30°, то и отражается он под тем же углом 30°.
Изучаем преломление света
Рассмотрим случай, показанный на рис. 20.2. Свет падает на стеклянную пластинку под определенным углом \( \theta_1 \) к нормали (см. предыдущий раздел), а входит в стекло уже под углом \( \theta_2 \) к нормали.
Преломление света по закону Снелла
Как с точки зрения физики правильно рассчитать такое изменение направления распространения света в стеклянной пластинке? Физикам известно, что углы \( \theta_1 \) и \( \theta_2 \) связаны следующей формулой:
Что такое \( n_1 \) и \( n_2 \)? Это так называемые показатели преломления. Изменение направления распространения света при пересечении границы между разными веществами называется преломлением света. Разные материалы могут обладать разными показателями преломления.
Закон физики, который описывает изменение направления распространения света при пересечении границы между разными веществами, называется законом Снелла преломления света. (Он был открыт в начале XVII-ro века голландским математиком Виллебрордом Снеллом, или Снеллиусом. — Примеч. ред.) Этот закон утверждает, что когда луч света падает под углом \( \theta_1 \) между падающим на поверхность лучом и нормалью к границе раздела двух сред с показателями преломления \( n_1 \) и \( n_2 \), то угол \( \theta_2 \) между прошедшим через границу лучом и нормалью к поверхности будет таким, что \( n_1\sin\theta_1=n_2\sin\theta_2 \). Например, показатель преломления воздуха в нормальных условиях 1,0002926 приблизительно равен показателю преломления вакуума 1 (точная величина). В большинстве случаев показатель преломления стекла приблизительно равен 1,5, поэтому можно сказать, что если \( \theta_1 \) = 45° для случая, показанного на рис. 20.2, то:
или
С помощью последнего равенства можно найти \( \theta_2 \):
Получается, что \( \theta_2 \) = 28,1°. Иначе говоря, свет преломляется по отношению к нормали так, как показано на рис. 20.2.
Измеряем глубину водоема на глазок
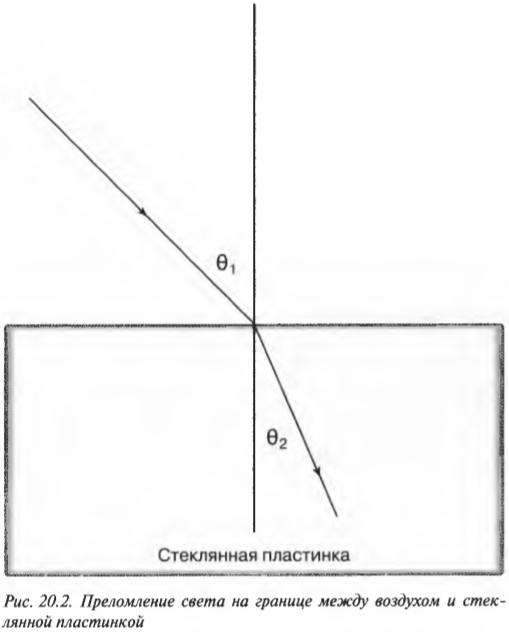
На рис. 20.2 показан рыбак, который прицелился острогой в рыбу, плавающую в воде. Луч света, отразившись от рыбы, пересекает границу между водой и воздухом и преломляется на ней. Рыбак подсознательно предполагает, что луч света от рыбы идет прямолинейно и поэтому считает, что она находится на кажущейся глубине, показанной на рисунке. Однако это не так.
Воображаемую и настоящую глубину можно связать следующим равенством:
Не забывайте, что \( n_1 \) — это показатель преломления материала, из которого свет выходит (в данном случае это вода), а \( n_2 \) — показатель преломления материала, в который света входит (в данном случае это воздух).
Например, если рыбаку кажется, что рыба находится на глубине 2 м, а показатель преломления воды примерно равен 1,33 (у воздуха он равен 1), тогда:
Преломление и скорость света
Показатель преломления материала в действительности является отношением скорости света в вакууме, деленной на скорость света в материале:
п = (скорость света в вакууме)/(скорость света в материале).
Итак, когда говорят, что показатель преломления стекла равен 1,5, то подразумевают — свет “путешествует” через стекло в 1,5 раза медленнее.
Итак, подставив в формулу числа, получаем:
В действительности рыба находится на глубине 2,66 м.
Всего лишь зеркала и ничего более
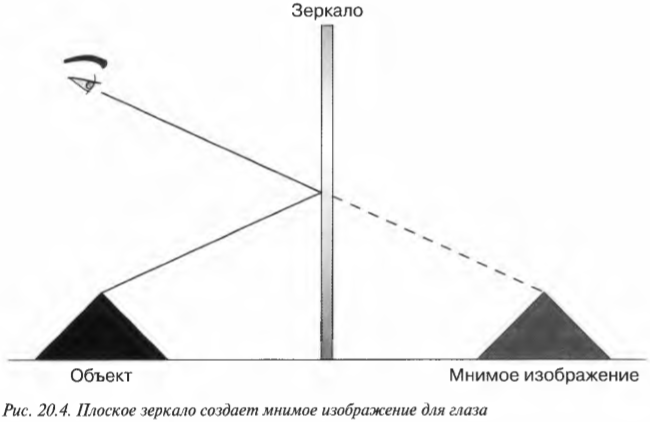
В повседневной жизни зеркала окружают нас всюду. Что происходит, когда мы смотрим на них? На рис. 20.4 показан пример отражения света в плоском зеркале. Некий объект находится перед зеркалом, а свет от него, отразившись от зеркала, попадает в глаз. Впрочем, с точки зрения глаза свет пришел от объекта, расположенного за зеркалом, причем на том же расстоянии от зеркала, что и настоящий объект, находящийся перед зеркалом. Однако на самом деле никакого объекта за зеркалом нет, поэтому изображение в зеркале называют мнимым изображением действительного объекта.
С плоским зеркалом все легко и просто. Но что происходит в случае отражения света в искривленном зеркале?
Увеличиваем объект с помощью вогнутого зеркала
Для анализа отражения света от искривленного зеркала придется приложить гораздо больше усилий. Обратите внимание на зеркало, показанное на рис. 20.5. Оно имеет вогнутую форму, т.е. похоже на часть внутренней стороны сферы.
Вогнутое зеркало легко представить, если вспомнить внутреннюю форму обыкновенной чашки, подобную “вогнутому” зеркалу.
Итак, что же происходит, если поместить объект рядом с вогнутым зеркалом?
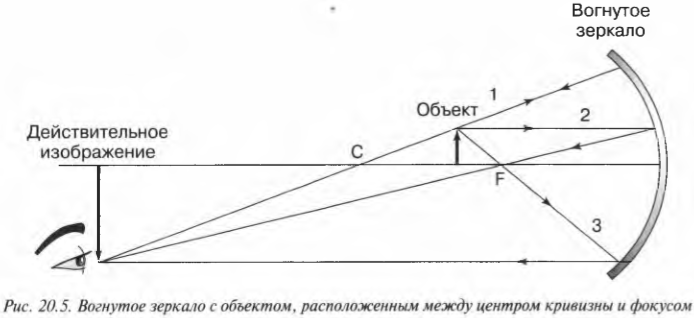
Для вогнутых зеркал особую важность представляют две точки: центр кривизны и фокус, обозначаемые соответственно как \( C \) и \( F \). Точка \( C \) располагается на горизонтальной оси \( CF \) на расстоянии, равном радиусу кривизны \( R \) сферической поверхности, частью которой является зеркало.
В точке \( F \) фокусируются (т.е. собираются) лучи света, падающие в зеркало параллельно горизонтальной оси \( CF \) (на небольшом расстоянии от нее). Для вогнутого зеркала \( f= R /2 \), где \( f \) — это расстояние от зеркала до точки \( F \) по горизонтальной оси \( CF \). На рис. 20.5 объект показан между центром кривизны сферической поверхности и фокусом зеркала. Где появится изображение объекта в этом случае? Для этого потребуются дополнительные сведения, т.е. физические формулы.
Строим схемы хода лучей света
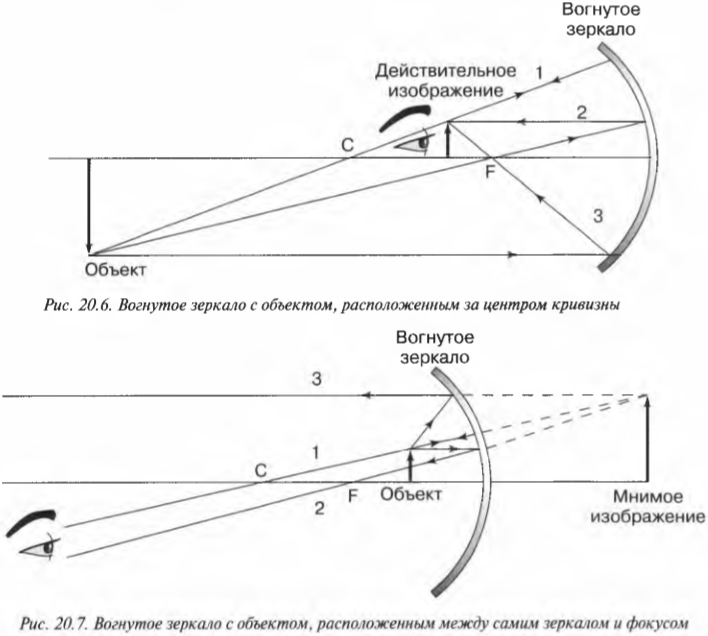
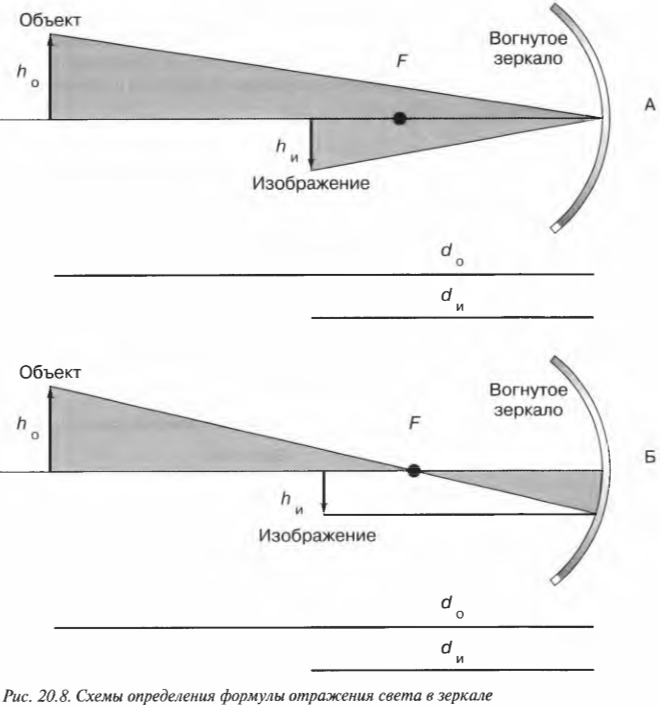
Чтобы найти изображение объекта, размещенного между центром кривизны и фокусом, используем три луча света, показанные на рис. 20.5 и обозначенные цифрами 1, 2 и 3. Эти три луча света выходят из объекта, отражаются от зеркала и пересекаются на изображении объекта. Вот как проходят эти лучи от объекта до его изображения в зеркале:
- луч 1 выходит из объекта, отражается от зеркала и проходит через центр кривизны;
- луч 2 выходит из объекта горизонтально по направлению к зеркалу, отражается от него и проходит через фокус;
- луч 3 идет из объекта через фокус, отражается от зеркала и идет параллельно горизонтальной оси.
Точка пересечения трех лучей и является местом, где находится изображение. На рис. 20.5 можно видеть, что изображение находится за центром кривизны; по сравнению с самим объектом оно является обратным (перевернутым) и увеличенным. Так как изображение находится по ту же сторону от зеркала, что и объект, оно называется действительным изображением. В месте появления действительного изображения можно поместить экран, на котором будет фокусироваться лучи света от объекта, создавая, таким образом, его изображение.
Теперь рассмотрим противоположный случай — когда объект находится далеко от центра кривизны (рис. 20.6). Где изображение окажется на этот раз? Воспользуемся теми же тремя лучами, как показано на рис. 20.6. Сейчас изображение располагается между центром кривизны и фокусом; оно прямое (не перевернутое), имеет уменьшенные размеры и тоже является действительным изображением.
Есть ли еще другие варианты размещения объекта? Да, объект может находиться еще ближе к зеркалу — между фокусом и самим зеркалом (как показано на рис. 20.7). Если проанализировать ход тех же трех лучей, то можно обнаружить, что они пересекаются не перед зеркалом, а, как видно на рисунке, за ним. Дело в том, что это изображение является мнимым: в действительности для его создания лучи света не пересекаются. На самом деле лучи, отражающиеся от зеркала, кажутся идущими от мнимого изображения, расположенного за зеркалом.
Анализируем ход лучей
При наличии формул можно легко вычислить место, где появится изображение объекта, полученное с помощью вогнутого зеркала. На рис. 20.8 показаны две схемы отражения объекта в зеркале.
Введем следующие обозначения для некоторых наиболее важных величин:
- \( h_о \) — высота объекта;
- \( h_и \) — высота изображения;
- \( d_о \) — расстояние до объекта;
- \( d_и \) — расстояние до изображения.
Составим формулу, связывающую все эти величины, обращая внимание на то, что все треугольники, показанные на схеме А (рис. 20.8), являются подобными, и что все треугольники, показанные на схеме Б того же рисунка, также являются подобными. Как известно, у подобных треугольников одинаковые углы, а соотношения длин сторон сохраняются.
Из схемы А, согласно закону отражения (угол падения равен углу отражения), можно вывести следующее соотношение:
Аналогично, из схемы Б получаем, что:
Приравняв правые части этих равенств, получаем:
Иначе говоря, имеем:
Эта так называемая формула сферического зеркала; она связывает расстояние от предмета до зеркала и фокусное расстояние с расстоянием между зеркалом и образуемым изображением. Если изображение мнимое (образуется за пределами зеркала), то значение \( d_и \) будет отрицательным.
Допустим, что представители косметической компании предлагают создать зеркало для ванной, в котором люди выглядели бы больше, чем на самом деле, но чтобы полученное изображение не было обратным.
Попробуем решить эту задачу с помощью рис. 20.7. Если расположить лицо между зеркалом и фокусом, то в зеркале можно будет наблюдать увеличенное мнимое изображение. Допустим, что лицо находится на расстоянии 12 см от зеркала, зеркало имеет радиус кривизны 40 см, т.е. имеет фокусное расстояние 20 см. Где же появится мнимое изображение? Воспользуемся уже известной нам формулой:
Подставив в нее числа, получим:
Решением полученного уравнения будет \( d_и \) = -30 см.
Теперь смело можно сказать представителям косметической компании, что при использовании зеркала с радиусом кривизны 40 см изображение появится на расстоянии -30 см.
Предположим, что, выслушав вас, они переглянутся и спросят: “Ну а как насчет увеличения?” Хороший вопрос.
Вычисляем увеличение вогнутого зеркала
Увеличение \( m \) зеркала — это отношение высоты изображения и высоты объекта, т.е. \( h_и/h_о \). Именно этот параметр зеркала больше всего интересует представителей косметической компании.
Поскольку
то, таким образом, получим:
Следует отметить, что если увеличение положительное, то изображение прямое, а если отрицательное, то — обратное. Итак, каким будет увеличение косметического зеркала, разработанного в предыдущем разделе? Итак, изображение появляется на расстоянии — 30 см, когда высота объекта равна 12 см, поэтому:
Итак, если лицо находится на расстоянии 12 см от зеркала, то увеличение зеркала равно 2,5.
Уменьшаем объект с помощью выпуклого зеркала
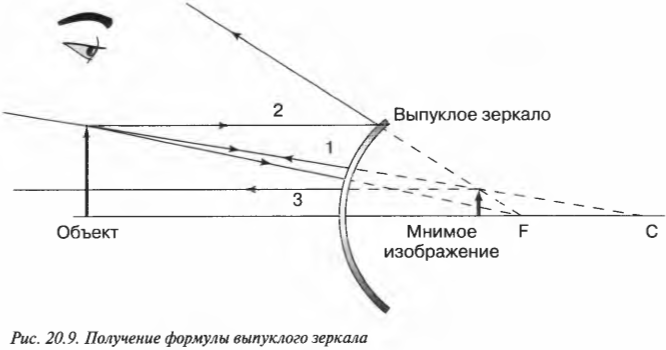
Выпуклое зеркало похоже на часть наружной поверхности зеркальной сферы (рис. 20.9). Как описать его свойства с точки зрения физики?
Никаких проблем. Опять, как и в случае вогнутого зеркала в предыдущем разделе, следует использовать три луча. Разница лишь в том, что в выпуклом зеркале изображение всегда мнимое, а фокус и центр кривизны зеркала всегда располагаются по ту сторону зеркала, где нет объекта.
На рис. 20.9 показано, что полученное изображение является мнимым (находится за зеркалом), прямым и уменьшенным. Это утверждение легко проверить с помощью любой выпуклой блестящей поверхности, например с помощью металлической салатницы. Посмотрите на свое отражение в салатнице (с ее наружной стороны), и вы увидите свое уменьшенное (и немного искаженное) изображение.
Для выпуклых зеркал можно использовать ту же формулу зеркала, которая была получена ранее для вогнутых зеркал. Не забывайте только вот о чем: поскольку фокус располагается за зеркалом, то величина \( f \) является отрицательной. Допустим, что имеется выпуклое зеркало с фокусным расстоянием -20 см, а объект находится перед зеркалом на расстоянии 35 см. Где появится изображение? Достаточно в формулу зеркала:
подставить значения:
Решением полученного уравнения будет:
Изображение появится по другую сторону зеркала на расстоянии 12,7 см. А увеличение? Из предыдущего раздела известно, что:
Таким образом, получим:
Мнимое изображение будет прямым, уменьшенным с коэффициентом 0,36 и расположенным по другую сторону от зеркала на расстоянии 12,7 см. Итак, мы овладели некоторыми секретами зеркал, но чтобы постичь оптику и стать настоящим “хозяином” ее законов, нужно познакомиться еще со многими другими явлениями.
Смотрим сквозь линзы
Кроме зеркал, другими оптическими элементами, с которыми вы сталкиваетесь каждый день, являются линзы. Линзы специально делаются для того, чтобы искривлять проходящий через них свет, фокусируя его и создавая изображения. И подобно зеркалам, линзы могут создавать действительные и мнимые изображения. Здесь мы рассмотрим линзы двух видов: собирающие и рассеивающие.
Увеличиваем объект с помощью собирающих линз
Собирающая линза отклоняет лучи света по направлению к горизонтальной оси. Луч света от объекта, расположенного по одну сторону линзы, фокусируется в действительное изображение, расположенное по другую ее сторону. Наверняка вам приходилось рассматривать мелкие объекты, например насекомых, используя увеличительное стекло? Это увеличительное стекло и является собирающей линзой.
Строим схему хода лучей в линзе
Схемы лучей применяются к линзам во многом так же, как и к зеркалам. На рис. 20.10 показана типичная схема хода лучей в собирающей линзе.
Чтобы найти изображение объекта, размещенного дальше радиуса кривизны, снова используем три луча света, которые пронумерованы на рис. 20.10 цифрами 1, 2 и 3. Эти три луча света выходят из объекта, проходят сквозь линзу и пересекаются на изображении объекта. Вот как проходят эти лучи от объекта до его изображения в линзе:
- луч 1 выходит из объекта и проходит через центр линзы;
- луч 2 выходит из объекта горизонтально по направлению к линзе, а затем проходит через фокус;
- луч 3 идет из объекта через фокус, затем проходит через линзу и идет параллельно горизонтальной оси.
Пользуясь этими сведениями, теперь можно создать схему хода лучей для случая, показанного на рис. 20.10, когда объект находится дальше радиуса кривизны. Как известно, радиус кривизны \( R=2f \), где \( f \) — это фокусное расстояние. В этом случае получается уменьшенное действительное обратное изображение. Поскольку в реальных линзах часто используется несферическая поверхность, то радиус кривизны в них лишь приблизительно равен \( 2f \), но для малых линз эти два значения достаточно близки.
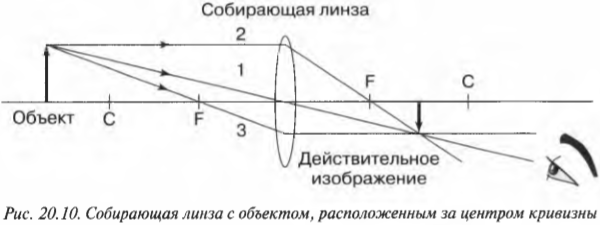
Допустим, что объект находится между центром кривизны \( C \) и фокусом \( F \), как показано на рис. 20.11. Каким будет изображение объекта? Чтобы найти его, снова используем три луча света: в результате получится увеличенное действительное обратное изображение.
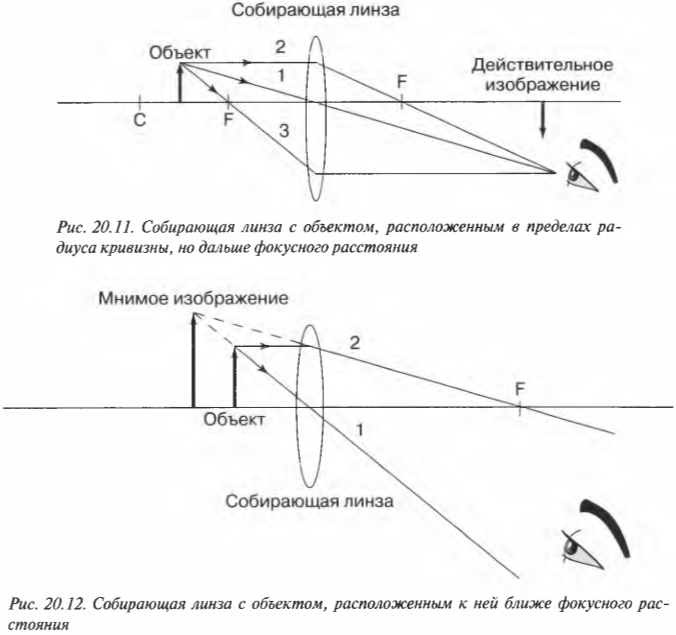
Рассмотрим последний случай, когда объект находится к линзе ближе, чем фокусное расстояние, как показано на рис. 20.12. В таком случае с помощью лучей 1 и 2, показанных на том же рисунке, можно определить, что получится мнимое прямое и увеличенное изображение (именно так и работают увеличительные стекла). На всех схемах хода лучей видно, что все три луча сходятся вместе, создавая изображение.
Мнимые изображения отличаются тем, что в том месте, где находится такое изображение, на самом деле никакие лучи света не сходятся. Если поместить там экран, то на нем нельзя будет увидеть никакого изображения. Изображение является мнимым, т.е. чтобы его увидеть, надо смотреть сквозь линзу — в ней-то и будет видно это изображение.
Выводим формулу линзы
Как рассчитать, где все-таки находится изображение объекта, рассматриваемого через линзу? Для этого используется формула тонкой линзы. Она похожа на формулу зеркала и может быть выведена тем же способом:
где \( d_о \) и \( d_и \) — соответственно расстояния от линзы до объекта и изображения, а \( f \) — фокусное расстояние.
Это равенство соблюдается для тонких линз (в противном случае форма линз, которая для этой формулы предполагается сферической, приводит к так называемой сферической аберрации). Обратите внимание, что если изображение мнимое, то значение \( d_и \) будет отрицательным.
Допустим, что нужно рассмотреть почтовую марку с помощью увеличительного стекла с собирающей линзой с фокусным расстоянием 5 см, которую удобно держать на расстоянии 3 см от марки. Где появится мнимое изображение? Все, что надо сделать: это в предыдущую формулу
подставить значения
Решением полученного уравнения будет \( d_и \) = -7,5 см. Отрицательное расстояние до изображения означает, что изображение мнимое. Как показано на рис. 20.12, оно будет увеличенным и прямым.
Раз уж мы работаем с увеличительным стеклом, то попробуем найти его увеличение.
Вычисляем увеличение линзы
Найти увеличение собирающей линзы нетрудно. Как и для зеркал, его можно вычислить по следующей формуле:
Если увеличение отрицательное, то действительное изображение по отношению к объекту будет обратным, а если увеличение положительное, то действительное изображение будет прямым. Для мнимых изображений все наоборот, поскольку нужно учитывать отрицательный знак координаты мнимого изображения.
Чему же равно увеличение линзы из примера в предыдущем разделе? Как известно, \( d_о \) = 3 см и \( d_и \) = -7,5 см, поэтому:
Увеличение для почтовой марки, расположенной в 3 см от увеличительного стекла, будет равно -2,5.
Вот еще один пример. Допустим, что надо получить действительное увеличенное изображение, чтобы спроецировать его на экран. Для этого можно использовать проектор с подсветкой слайдов, которые проецируются на экран, расположенный в 1 м от линзы проектора. В данном случае нужно использовать схему на рис. 20.11, когда объект находится в пределах радиуса кривизны (равного \( 2f \)), но дальше фокусного расстояния (равного \( f \)).
Предположим, что слайд находится в 10 см от линзы. Каким должно быть ее фокусное расстояние? Воспользуемся известной формулой тонкой линзы:
Подставив в эту формулу значения, получим:
Иначе говоря, получим:
или
Таким образом, фокусное расстояние нужной вам линзы примерно равно 9 см.
Уменьшаем объект с помощью рассеивающей линзы
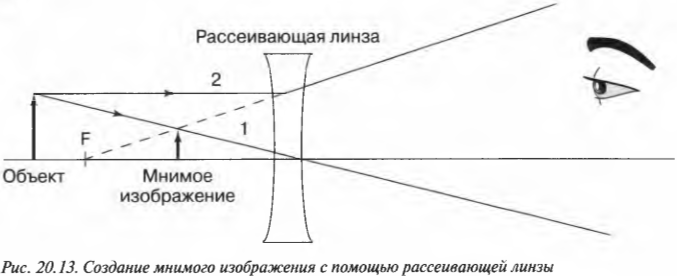
Собирающие линзы фокусируют световые лучи по направлению к горизонтальной оси, а рассеивающие линзы, наоборот, “расфокусируют” их от этой оси. На рис. 20.13 показана схема хода лучей в рассеивающей линзе, согласно которой образуется мнимое прямое уменьшенное изображение.
Рассеивающая линза всегда создает мнимое прямое уменьшенное изображение объекта.
Можно ли здесь применить известную нам формулу тонкой линзы, как для собирающих линз? Конечно можно, надо только помнить, что фокусное расстояние рассеивающей линзы отрицательно, как у выпуклого зеркала.
Допустим, что объект находится на расстоянии 4 см от рассеивающей линзы с фокусным расстоянием -10 см. Где появится изображение? Возьмем формулу тонкой линзы:
и подставим в нее имеющиеся данные:
После несложных преобразований получим:
Обратите внимание, что изображение находится к линзе ближе, чем фокус, и на отрицательном расстоянии, следовательно, изображение мнимое (рис. 20.13). Чему равно увеличение этой линзы? Воспользуемся той же формулой увеличения, которая применялась для собирающих линз (см. предыдущий раздел):
Подставив в нее числа, получим:
Отрицательное увеличение означает, что данное мнимое изображение по отношению к объекту является прямым. Кроме того, увеличение меньше 1, т.е. по своим размерам мнимое изображение меньше объекта.






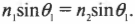
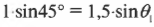
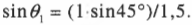
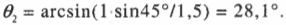
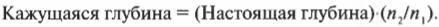
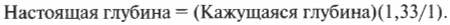
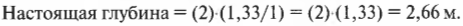
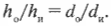
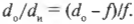
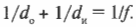
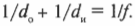
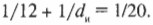
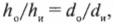
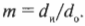
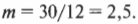
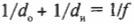
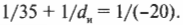
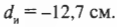
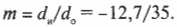
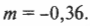
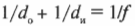
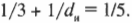
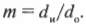
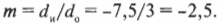
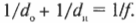
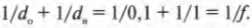
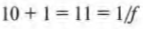
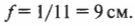
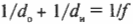
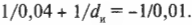
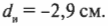
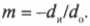
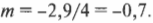
Добавить комментарий