Глава 19. Усмиряем колебания тока и напряжения

В этой главе…
- Генерируем электрический ток, перемещая проводник
- Ловим магнитный поток
- Определяем направление магнитной индукции по правилу Ленца
- Учитываем индуктивность и емкость при переменном токе
- Вычисляем сопротивление колебательного контура
В этой главе мы приступаем к изучению переменного тока, т.е. электрического тока с переменным напряжением и силой тока. Этот ток обладает необычным сопротивлением, которое зависит от частоты, и называется электрическим импедансом. Но импеданс — это всего лишь один из многих “деликатесов” этой главы. В ней также рассказывается об индуктивном и емкостном сопротивлениях, создаваемых конденсаторами и катушками индуктивности, а также о других свойства электрических цепей с переменным током.
Содержание
Индуцируем электродвижущую силу
Если попробовать изменить магнитный поток (см. главу 18) через поверхность, ограниченную проводящим контуром, то в нем возникнет электродвижущая сила (э.д.с.), которая пропорциональна скорости изменения магнитного потока. Электрический ток, вызванный этой ЭДС, называется индукционным током, а само явление — электромагнитной индукцией.
Магнитный поток можно представить, как некое количество линий магнитного поля, проходящих перпендикулярно поверхности.
Попробуем найти э.д.с. электромагнитной индукции проводящего контура со стержнем, движущимся в магнитном поле (рис. 19.1). Напряжение (э.д.с. электромагнитной индукции) индуцируется в стержне именно благодаря движению стержня в магнитном поле. Как результат, в замкнутом проводящем контуре возникнет электрический ток. Пусть металлический стержень имеет длину 1 м и движется со скоростью 100 км/ч (примерно 28 м/с) в магнитном поле 1 Тл. Какое напряжение будет на краях стержня, если он движется под прямым углом к магнитному полю? Надо только подставить значения в следующую формулу:
Под прямым углом на краях стержня будет напряжение около 28 В. Как получена эта формула?
Создаем напряжение, двигая проводник в магнитном поле
На рис. 19.1 металлический стержень-проводник движется со скоростью v вправо по металлическим направляющим и находится в магнитном поле, направленном от читателя перпендикулярно к плоскости страницы. Что происходит с точки зрения физики?
Электрический заряд \( q \) внутри металлического стержня движется в магнитном поле со скоростью \( v \), поэтому на него действует сила:
где \( q \) — электрический заряд и \( B \) — магнитная индукция.
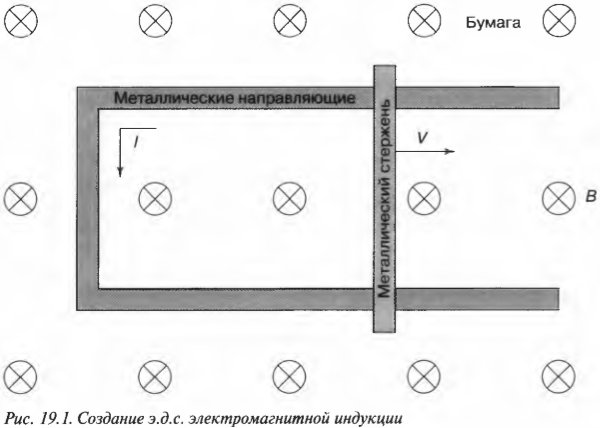
Именно эта сила индуцирует электрический ток. Ей соответствует напряженность электрического поля \( E \), которая вычисляется по следующей формуле:
Работа \( A \) по перемещению заряда \( q \) на расстояние \( L \) в таком электрическом поле определяется формулой:
Откуда получаем формулу для напряжения (см. определение напряжения в главе 16):
Выражаем напряжение через изменение площади контура
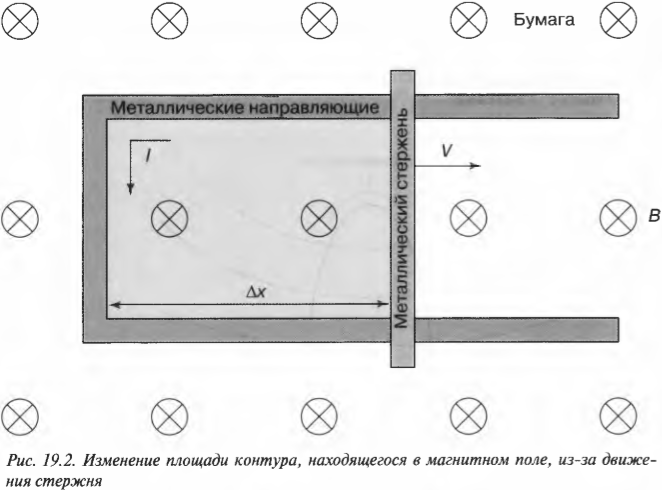
Посмотрим, как меняется площадь контура в примере на рис. 19.1. Пусть за время \( \Delta t \) металлический стержень проходит через магнитное поле расстояние \( \Delta x \). Можно сказать, что \( v= \Delta x/\Delta t \), в результате чего:
Теперь посмотрим, что собой представляет произведение \( \Delta xL \). Это расстояние, которое стержень проходит за некоторое время, умноженное на длину этого стержня. Взглянув на рис. 19.2, вы увидите, что \( \Delta xL \) равно площади \( \Delta S \), покрываемой стержнем за время движения (эта площадь заштрихована).
Итак, если стержень за время \( \Delta t \) проходит расстояние \( \Delta x \), то изменение площади замкнутой области равно \( \Delta S=\Delta xL/\Delta t \). Тогда формулу э.д.с. электромагнитной индукции можно записать таким образом:
Вычисляем электромагнитную индукцию с помощью закона Фарадея
В предыдущей формуле для вычисления э.д.с. электромагнитной индукции:
величина \( B\Delta S \) называется магнитным потоком. Магнитный поток — это мера того, какой поток вектора магнитной индукции проходит через некоторую поверхность. Например, при увеличении вдвое магнитной индукции, ее поток также удвоится. Единицей измерения магнитного потока в системе СИ является вебер (Вб), 1 Вб = Тл·м2, а обозначается магнитный поток греческой буквой \( \mathbf{Ф} \). (В системе СГС единицей магнитного потока является максвелл (Мкс); 1 Вб = 108 Мкс.)
Таким образом, формула э.д.с. индукции:
преобразуется в:
где изменение магнитного потока \( \Delta \mathbf{Ф}=\Delta S/\Delta t \).
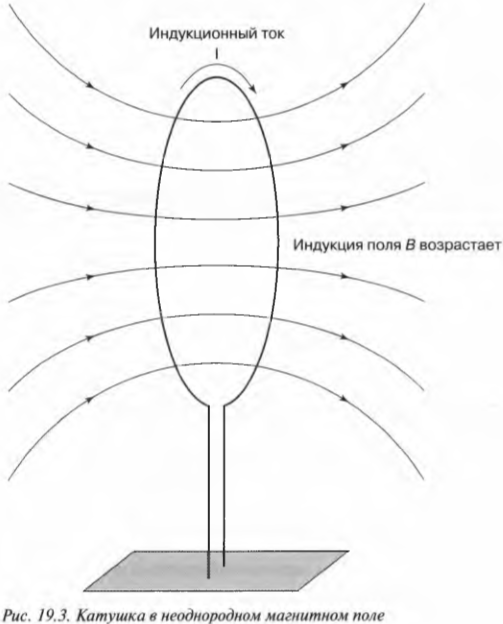
Из последней формулы следует, что создаваемая э.д.с. электромагнитной индукции — это скорость изменения магнитного потока. Впрочем, это еще не окончательная формула. Ее обычно пишут со знаком “минус” (об этом знаке, который появляется благодаря правилу Ленца, более подробно говорится в следующем разделе):
Знак “минус” означает, что создаваемая э.д.с. электромагнитной индукции в свою очередь создает ток, который будет сопротивляться изменению магнитного потока. Эта формула называется законом Фарадея. Обычно в формулировке этого закона используется магнитный поток, проходящий через катушку с \( N \) витками.
Если имеется катушка с \( N \) витками и проходящий через нее магнитный поток изменяется, то по закону Фарадея создаваемая в этой катушке э.д.с. электромагнитной индукции вычисляется по формуле:
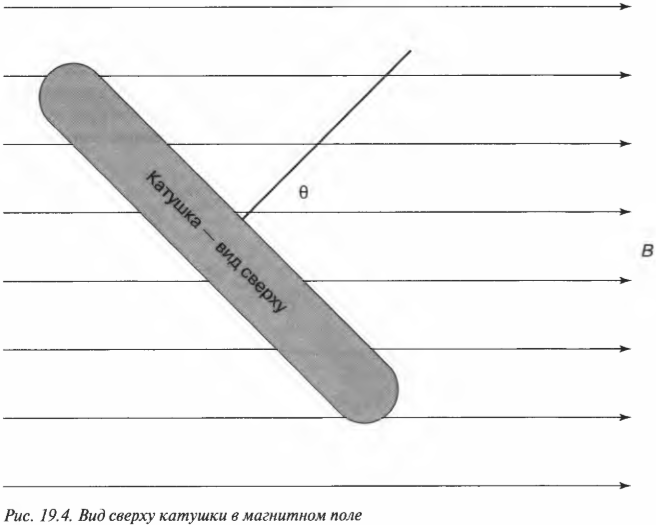
Каким образом в катушке меняется магнитный поток, если ее размеры не меняются? Это происходит благодаря изменению либо величины магнитного поля, либо площади поверхности, которую пронизывает магнитное поле. На рис. 19.4 показан вид сверху на катушки, расположенную под углом к вектору магнитной индукции. Таким образом, при изменении угла \( \theta \) меняется и поток, проходящий через катушку
Как видите, э.д.с. электромагнитной индукции может создаваться в катушке двумя способами: при изменении величины магнитного поля или при изменении угла между катушкой и линиями магнитной индукции, т.е. площади контура, а значит, и магнитного потока, который пронизывает контур.
Определяем знак с помощью правил Ленца
Когда магнитное поле пронизывает контур, в нем генерируется э.д.с. электромагнитной индукции, т.е. тратится определенная энергия на создание электрического поля. А после его создания вся эта система противится любым изменениям.
Если создать громадное магнитное поле, пронизывающее проволочный контур, а потом внезапно выключить источник магнитного поля, то можно заметить, что проходящее через контур магнитное поле исчезает не сразу, а постепенно. Почему это происходит? Дело в том, что появившаяся э.д.с. электромагнитной индукции заставляет ток течь таким образом, чтобы он сохранял достигнутое стабильное состояние, т.е. сохранял магнитное поле неизменным.
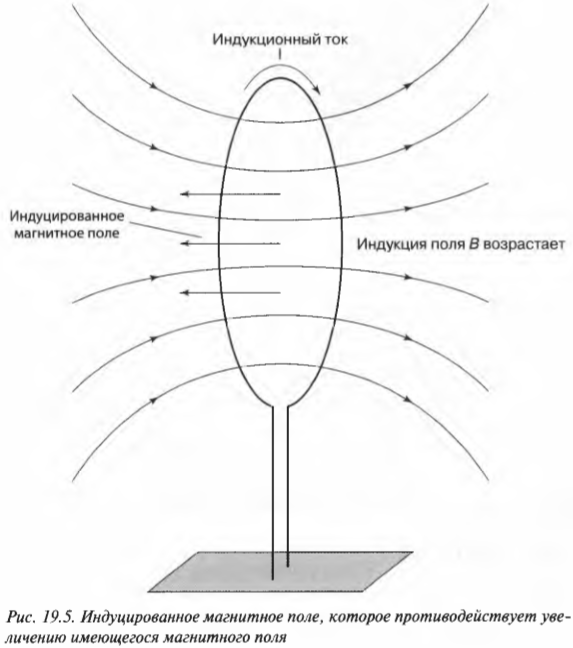
В этом и состоит суть правила Ленца: э.д.с. электромагнитной индукции будет действовать так, чтобы полученный в результате ток создавал индуцированное магнитное поле, противодействующее изменению потока.
Пусть пронизывающее контур магнитное поле меняется с течением времени, как показано на рис. 19.5. Тогда э.д.с. электромагнитной индукции будет действовать так, чтобы сохранить существующее положение, т.е. будет создавать индуцированное магнитное поле, которое, как показано на рис. 19.5, противодействует увеличению уже имевшегося магнитного поля.
Обратите внимание на направление индукционного тока в контуре. Если направить пальцы правой руки (кроме большого, отставленного в сторону) вдоль витков катушки по ходу движения тока, то большой палец этой руки будет указывать в направлении индуцированного магнитного поля (подробнее о правиле правой и левой руки можно узнать в главе 18). Именно это поле будет противодействовать увеличению магнитного поля, уже приложенного к катушке.
Зная правило Ленца, всегда можно определить направление индукционного тока — он направлен так, чтобы сохранить существующее положение. Если магнитный поток увеличивается, то индукционный ток создает индуцированное магнитное поле, которое старается не дать потоку увеличиться. А если магнитный поток уменьшается, то индукционный ток направлен так, чтобы, наоборот, увеличить поток.
Попробуйте проверить только что полученные знания с помощью рис. 19.5. Куда направлен ток, если внешний магнитный поток, пронизывающий контур, увеличивается с течением времени?
Вычисляем индуктивность
Насколько сильно контур может противодействовать изменению идущего через нее магнитного потока? Эта способность к противодействию определяется ее индуктивностью. Что это такое?
Если в проводящем контуре течет ток силой \( I \), создающий магнитное поле, то величина магнитного потока \( Ф \), пронизывающего контур, связана с величиной тока следующим образом:
Коэффициент пропорциональности \( L \) называется индуктивностью (или, строго говоря, коэффициентом самоиндукции контура. — Примеч. ред.). Индуктивность зависит от размеров и формы контура, а также от магнитной проницаемости окружающей среды.
Известный закон Фарадея (см. выше), согласно которому э.д.с. электромагнитной индукции пропорциональна изменению потока через катушку с \( N \) контурами-витками
перепишем в несколько другой форме. Изменим эту формулу, введя в нее индуктивность:
где \( L_{кат} \) — индуктивность всей катушки с \( N \) контурам и-витками.
Здесь все \( N \) витков катушки пронизывает суммарный магнитный поток \( NФ \), который пропорционален силе тока \( I \), идущего через катушку, с коэффициентом пропорциональности \( L_{кат} \), т.е. \( NФ=L_{кат}I \).
В системе СИ индуктивность измеряется в генри (Гн), 1 Гн = 1 Вб/1 А.
Величина \( L \) — это не просто коэффициент пропорциональности, а коэффициент самоиндукции контура. Он показывает, как сильно контур может реагировать на изменение потока. При изменении силы тока, идущего через него, получаем изменение магнитного потока, и чем больше \( L \), тем лучше контур противодействует изменению тока, создавая свой собственный ток. Это значит, что контур может противодействовать внезапным изменениям идущего через него тока, так как его индуктивность старается противодействовать любому изменению потока. По этой причине катушки, используемые в электрических цепях, называются катушками индуктивности.
В главе 16 описываются некоторые элементы цепи, работающие с электрическими полями, а именно резисторы и конденсаторы. Теперь к ним добавился еще один тип элемента цепи, а именно катушки индуктивности, которые обладают очень полезным качеством для применения их в электрических цепях. В конденсаторе заряд меняется не мгновенно, а постепенно, что позволяет плавно изменять напряжение в электрических цепях. Аналогично, сила тока, идущего через катушку индуктивности, также меняется не мгновенно, а постепенно, что позволяет плавно изменять ее в электрических цепях.
Изучаем цепи переменного тока и напряжения
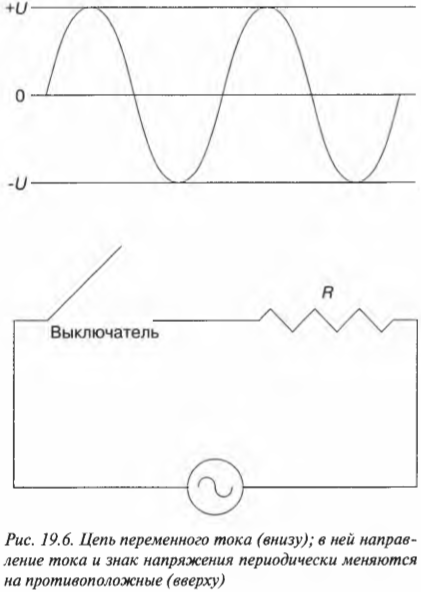
Уникальное поведение конденсаторов и резисторов в электрических цепях становится по-настоящему полезным, когда сила тока и напряжение меняются с течением времени — другими словами, когда приходится иметь дело с переменными токами и переменными напряжениями. Например, электрическое питание из домашней розетки характеризуется переменностью тока и напряжения. В переменном токе направление тока и знак напряжения периодически меняются на противоположные. На рис. 19.6 приведен пример электрической цепи переменного тока (внизу) и график зависимости напряжения от времени (вверху).
Внизу кружок с извилистой линией обозначает источник переменного тока, создаваемое им напряжение показано в верхней части рис. 19.6.
Оцениваем среднюю величину переменного напряжения
На что похоже переменное напряжение? Имеется много способов изменения напряжения с помощью электрических цепей, но самый распространенный способ генерирует синусоидальные колебания, показанные на рис. 19.6, как колебания переменного напряжения из домашней розетки.
Заимствуя кое-какие понятия вращательного движения (см. главу 7), напряжение можно выразить математически:
где \( U_0 \) — максимальное напряжение, \( f \) — частота колебаний напряжения (например, 50 Гц для тока из домашней розетки в странах СНГ), a \( t \) — время. Что собой представляет ток, создаваемый таким напряжением, если замкнуть выключатель? В цепи, показанной на рис. 19.6, единственным элементом (кроме выключателя, который можно считать простым проводником) является резистор (см. главу 17). Резистор не реагирует на изменение напряжения и силы тока, как это делают конденсаторы и катушки индуктивности. Для резистора не имеет значения, как меняется напряжение. Его сопротивление \( R \) остается постоянным и не зависит от скорости изменения напряжения и силы тока. Напряжение \( U \) и сила тока \( I \) на нем всегда связаны известным законом:
Поэтому сила тока выражается следующей формулой:
А как насчет мощности, рассеиваемой в цепи, т.е. мощности, которую резистор рассеивает в виде тепла? Из главы 17 известно, что мощность \( Р = IU \), но так как напряжение и сила тока меняются с течением времени, то нельзя сказать, что \( Р = I_0U_0 \). На самом деле мгновенная мощность переменного тока \( P_{мгн} \) определяется формулой:
Поскольку при усреднении за период последнее слагаемое становится равным нулю, то средняя мощность переменного тока \( P_{средняя} \) равна:
Часто эта формула записывается следующим образом:
Величины \( I_{эфф} \) и \( U_{эфф} \) называются эффективным (или действующим) значением силы тока и эффективным (или действующим) значением напряжения.
Нахождение действующих значений тока и напряжения
С помощью действующих значений тока и напряжения можно получить мощность, рассеиваемую в резисторе из электрической цепи, используя для этого одно из следующих выражений (в которых рассеиваемая мощность вычисляется теми же способами, что и для постоянных токов и напряжений):
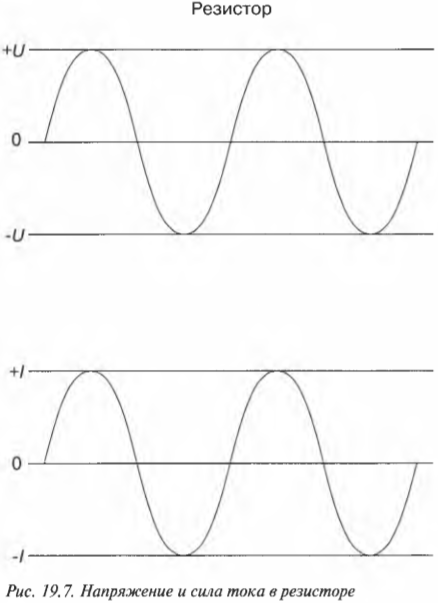
Резистор имеет дело с переменным током, для которого всегда верна формула \( U=IR \), если только \( U \) — это напряжение на концах резистора, а \( I \) — сила тока, идущего через него. Поэтому если формулой напряжения на концах резистора является:
то идущий через резистор ток вычисляется по формуле:
Таким образом, если в верхней части рис. 19.7 показано напряжение на концах резистора, тогда в нижней части этого рисунка показана сила тока, идущего через резистор.
Это достаточно просто, но как изменение напряжения и силы тока влияет на катушки индуктивности и конденсаторы?
Опережаем напряжение с помощью конденсаторов
На рис. 19.8 показана схема с конденсатором в цепи переменного тока. Из предыдущих разделов известно, что для резисторов в цепи переменного тока \( U_{эфф}=I_{эфф}R \). А как связать напряжение на концах конденсатора с идущим через него током?
С помощью следующей формулы:
Оно похоже на прежнюю формулу \( U_{эфф}=I_{эфф}R \), но что это еще за параметр \( R_c \)? Это емкостное сопротивление конденсатора, которое позволяет оценить, насколько при изменении частоты конденсатор может действовать, как резистор. Емкостное сопротивление измеряется в омах, как и сопротивление резистора, а на основе измерений, проведенных во время опытов, стало известно, что:
где \( f \) и \( C \) — это соответственно частота и емкость.
Измеряем силу тока, идущего через конденсатор
Зная приложенное к конденсатору напряжение, можно вычислить силу тока, идущего через него. Пусть емкость конденсатора на рис. 19.8 равна 1 мкФ (1 микрофарада, 1 мкФ = 10-6 Ф; подробнее о емкости и их единицах измерения см. главу 16), а эффективное значение подаваемого напряжения равно 12 В. Каким будет ток при частоте 10 Гц и 104 Гц? На основе приведенных выше формул:
получаем для 10 Гц:
а для 104 Гц:
Разница немалая, и все благодаря изменению частоты. Как видите, при работе с конденсаторами (в отличие от резисторов) надо всерьез учитывать частоту.
Смотрим на мгновенные значения
С помощью усредненных (действующих) значений можно эффективно работать с параметрами, мгновенные значения которых меняются с течением времени. Конденсатор попеременно заряжается и разряжается, не тратя энергию на тепло, т.е. в цепи переменного тока конденсатор в итоге не рассеивает попусту энергию (в отличие от резистора). Поскольку ток и напряжение меняются с течением времени, то хорошим показателем того, что происходит, является действующее значение (которое представляет собой среднее значение за период колебания). Именно действующее значение напряжение 220 В указывается на обычной домашней розетке.
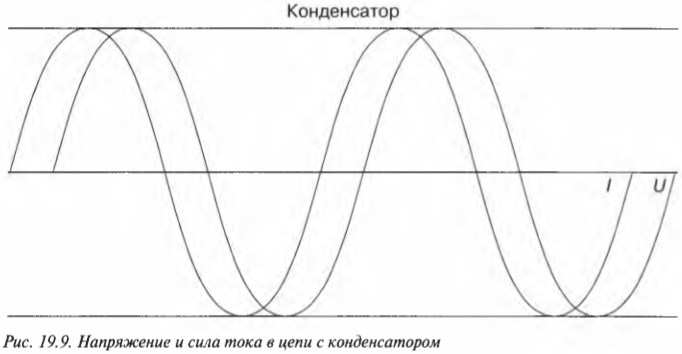
Рассмотрим теперь не эффективное, т.е. усредненное за какое-то время, значение, а реальное мгновенное, т.е. зависящее от времени, значение. На рис. 19.9 показан график напряжения от источника с рис. 19.8. Каким тогда будет график силы тока?
Как видно на рисунке, график силы тока имеет ту же форму, что и график напряжения, но немного сдвинут влево. Так как горизонтальная ось координат обозначает время, то видно, что сила тока достигает пика перед напряжением, или, как говорят физики, опережает напряжение. В действительности пиковые значения силы тока находятся на четверть периода впереди напряжения, следовательно, сила тока достигает определенной “высоты”, т.е. пикового значения, перед тем как это сделает напряжение. Итак, если:
(обратите внимание — вместо \( 2\pi\!f \) стоит \( \omega \), как в главе 7, когда речь шла об угловом движении), то:
Вот как можно прокомментировать эти выражения. Пусть сила тока достигла пика и начинает снижаться. Однако пройдя свой пик и уменьшаясь по величине, она пока еще остается положительной, т.е. продолжает накапливать заряд на конденсаторе. А так как напряжение конденсатора \( U = Q/C \), где \( Q \) и \( C \) — это соответственно заряд и емкость, то напряжение продолжает расти, пока сила тока положительная. Только когда сила тока становится отрицательной (после пересечения горизонтальной оси), заряд начинает с конденсатора уходить, и тогда напряжение начинает уменьшаться.
То, что сила тока опережает напряжение, на языке физики звучит так: сила тока и напряжение смещены по фазе. В резисторе, где \( U=IR \) и нет зависимости от времени, напряжение и сила тока всегда имеют одинаковую фазу. А в конденсаторе, где сила тока опережает напряжение на четверть периода, которая составляет \( \pi/2 \), сила тока и напряжение смещены по фазе на \( \pi/2 \). Это явление, наблюдаемое в конденсаторе, можно описать по-другому: сила тока опережает напряжение на \( \pi/2 \), или напряжение на \( \pi/2 \) отстает от силы тока.
Амплитуды напряжения и силы тока в конденсаторе могут принимать разные значения. На рис. 19.8 эти величины показаны с одинаковой амплитудой, чтобы можно было ясно видеть разность фаз.
Теперь перейдем к математике. Если напряжение, подаваемое на конденсатор, выражается формулой:
то, как известно:
В тригонометрии \( \sin(\omega t+\pi/2)=\cos(\omega t) \), поэтому:
Это равенство делает очень наглядной разность фаз в конденсаторе между напряжением и силой тока: эти величины меняются, как соответственно синус и косинус угла \( \omega t \), а синус и косинус смещены по фазе на 90°, т.е. на \( \pi/2 \).
Это равенство можно переписать с использованием \( U_0 \), например, так: \( I=(U_0/R_C)\!\cos(\omega t) \).
Отстаем от напряжения с помощью катушек индуктивности
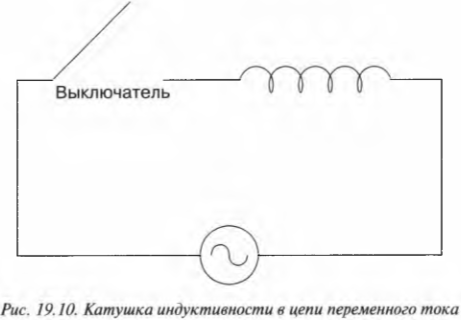
На рис. 19.10 показана волнистая штуковина, похожая на пружину. Так на электрических схемах обозначается катушка индуктивности, которая, подобно конденсаторам, реагирует на переменное напряжение.
Как реагирует катушка индуктивности на переменное напряжение? Так же, как и конденсатор:
но формула, связывающая эффективные значения напряжения и силы тока для катушки индуктивности, имеет такой вид:
Что такое \( R_L \)? Это индуктивное сопротивление катушки, которое показывает (во многом так же, как и сопротивление резистора), как сильно будет катушка сопротивляться изменению напряжения. Оно измеряется в омах и, как известно, равно:
где \( L \) — это индуктивность катушки, измеренная в генри (Гн). Индуктивное сопротивление прямо пропорционально индуктивности, а емкостное сопротивление обратно пропорционально емкости:
Как и конденсатор, катушка индуктивности попеременно накапливает электрический заряд и освобождается от него, не рассеивая на тепло никакой энергии в цепи переменного тока. Если напряжение, подаваемое от источника, зависит от времени по формуле:
то как себя ведет ток, проходящий через катушку индуктивности? Ответ можно увидеть на рис. 19.11. На этот раз сила тока отстает от напряжения, а напряжение, наоборот, опережает силу тока, т.е. имеем ситуацию, прямо противоположную той, что наблюдается с конденсатором.
Почему сила тока и напряжение смещены по фазе, причем в направлении, противоположном смещению по фазе у конденсаторов? Посмотрите на график, показанный на рис. 19.11.
Когда сила тока достигает своих максимальных и минимальных значений, ее изменение в этих точках равны нулю. Следовательно, напряжение электромагнитной индукции, которое учитывает все изменения магнитного потока в катушке, в этих точках также равно нулю. Поэтому сила тока и напряжение не совпадают по фазе. Если приложенное к катушке напряжение вычисляется по формуле:
то из-за отставания силы тока от напряжения ее формула будет такой:
В катушке индуктивности сила тока отстает от напряжения на четверть периода, а это значит, что сила тока достигает определенной высоты, например, своего пикового значения, уже после того, как это произойдет с напряжением.
Последнюю формулу еще можно записать таким способом:
Это равенство делает очень наглядной разность фаз в катушке индуктивности между силой тока и напряжением: эти величины меняются, как соответственно косинус со знаком “минус” и синус угла \( \omega t \), а косинус со знаком “минус” и синус смещены по фазе на 90°, т.е. \( \pi /2 \).
Это равенство можно переписать с использованием \( U_0 \), например, так: \( I=-(U_0/X_1)\!\cos(\omega t) \).
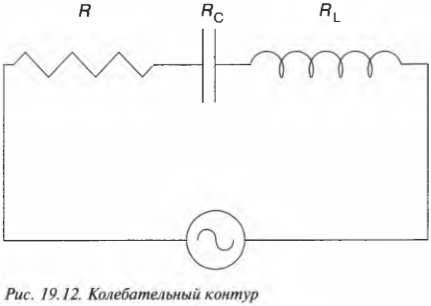
Боремся с тройным сопротивлением: колебательный контур
На рис. 19.12 показана типичная схема колебательного контура с “тройной угрозой” в одной электрической цепи: резистором, катушкой индуктивности и конденсатором.
Как оценить общее сопротивление подобной цепи? Теперь в ней нужно учесть сопротивление резистора (см. главу 17), а также емкостное и индуктивное сопротивления (см. предыдущие разделы в этой главе). Верна ли в таком случае формула:
Нет, к сожалению, не верна, так как с течением времени напряжение в резисторе, конденсаторе и катушке индуктивности меняются по-разному и их отдельные напряжения суммировать нельзя. Вместо этого придется ввести новую величину — импеданс \( Z \) (ее часто называют комплексным сопротивлением цепи):
Чему равен импеданс \( Z \)? Он вычисляется с помощью следующей формулы:
Пусть \( R_L \) = 16 Ом, \( R_C \) = 12 Ом, \( R \) = 3 Ом, а \( U_{эфф} \) = 10 В. Чему равно эффективное значение тока? Сначала находим импеданс \( Z \) по формуле:
Затем, используя равенство \( U_{действ}=I_{действ}Z \), получаем:
Действующее значение тока равно 2 А.
Кроме того, разность фаз тока и напряжения (т.е. отстает сила тока от напряжения или опережает его) можно определить по следующей формуле тангенса сдвига фазы \( \delta \) между силой тока и напряжением:






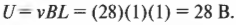
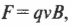
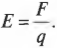
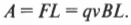
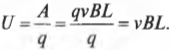
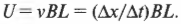
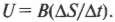
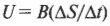
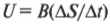
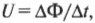
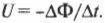
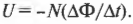
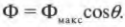
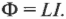
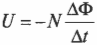
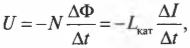
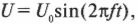
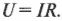
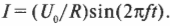
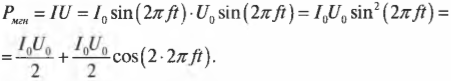
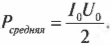
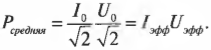
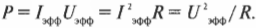
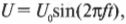
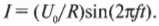

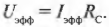
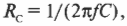
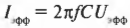
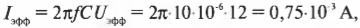
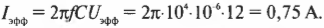
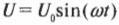
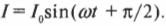
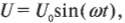
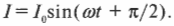
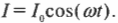
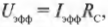
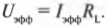
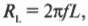
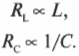
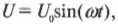
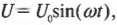
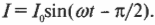
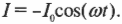
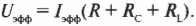
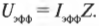
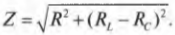
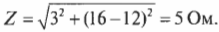
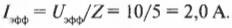
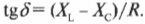
Добавить комментарий