Глава 21. Десять удивительных догадок теории относительности

В этой главе…
- Наблюдаем за поведением света на высоких скоростях
- Измеряем время и длину в пространстве
- Изучаем точку зрения Эйнштейна на вещество и энергию
- Проливаем свет на Солнце и скорость света
- Ищем связь между теориями Эйнштейна и Ньютона
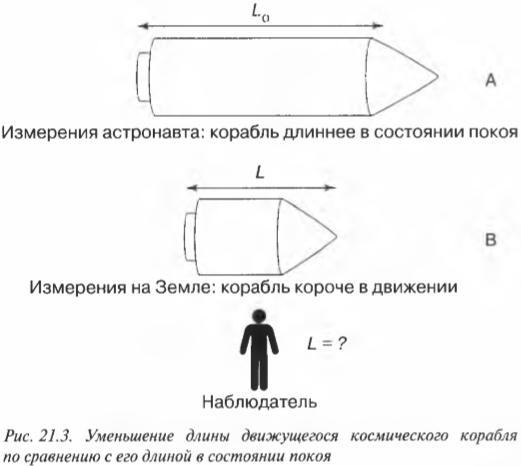
В этой главе описываются 10 удивительных физических фактов, относящихся к специальной теории относительности Эйнштейна. Строго говоря, эти физические сведения, в действительности, не являются “фактами”, потому что они, как и все остальные физические знания, однажды могут быть опровергнуты. Впрочем, специальная теория относительности была проверена тысячами способов и до сих пор не утратила своей ценности. С ее помощью можно сделать множество “эффектных” выводов. Например, вещество и энергия, оказывается, могут превращаться друг в друга, что описывается самой знаменитой (возможно) физической формулой:
Кроме того, оказывается, что при скорости, близкой к скорости света, время замедляется, а длина уменьшается. Обо всем этом рассказывается в данной главе. После знакомства с идеями Альберта Эйнштейна пространство и время уже трудно воспринимать как нечто неизменное.
Содержание
- У природы нет любимчиков
- Скорость света постоянна и не зависит от скорости его источника
- Замедление времени на высоких скоростях
- Космические путешественники стареют медленнее
- Уменьшение длины при высоких скоростях
- E=mc2 : эквивалентность вещества и энергии
- Вещество плюс антивещество получается взрыв
- Солнце «излучает массу»
- Скорость света превысить нельзя
- Ньютон до сих пор прав
У природы нет любимчиков
Много лет назад Эйнштейн утверждал, что в каждой инерциальной системе отсчета законы физики одинаковы. Если в инерциальной системе отсчета сумма всех сил, действующих на объект, равна нулю, то объект или остается неподвижным, или движется с постоянной скоростью. Другими словами, инерциальной называется система отсчета с нулевым ускорением. В ней соблюдается первый закон Ньютона: неподвижный объект продолжает быть неподвижным, а объект, движущийся равномерно, продолжает двигаться равномерно.
Неинерциальными являются вращающиеся или как-то по-другому ускоренные системы отсчета.
Попросту говоря, Эйнштейн сказал, что каждая из инерциальных систем отсчета хороша. С точки зрения физики среди систем отсчета для природы нет любимчиков. Чтобы проверить это, можно провести серию одинаковых физических экспериментов в неподвижной лаборатории и в равномерно движущемся железнодорожном вагоне (рис. 21.1).
Никто не увидит разницы в законах физики в обеих лабораториях. Ни один из экспериментов не даст возможность отличить две инерциальные системы отсчета, одна из которых неподвижна, а другая движется.
Скорость света постоянна и не зависит от скорости его источника
Очень тяжело сравнивать скорости машин, мчащихся по магистрали, не говоря уже о сравнении скоростей, близких к скорости света. Для большинства людей является довольно неожиданным фактом то, что скорость света постоянна, независимо от скорости движения измерительного прибора.
Предположим, что пассажир движущегося поезда, опустошив банку с напитком, бросает ее из вагона по ходу поезда и наблюдает за ней с помощью фонарика. Относительно поезда банка будет двигаться не слишком быстро, допустим, что со скоростью 10 км/ч, а свет фонарика— гораздо быстрее, а именно со скоростью, приблизительно равной 1079022156 км/ч.
Пусть поезд движется относительно неподвижного наблюдателя на перроне со скоростью 70 км/ч. Тогда банка, получив эту дополнительную скорость, пролетит мимо неподвижного наблюдателя со скоростью 80 км/ч. Ну и что? А то, что для света закон сложения скоростей имеет другой вид, и скорость света из фонарика относительно неподвижного наблюдателя будет всегда постоянной и приблизительно равной 1079022156 км/ч. Причем независимо от того, в каком направлении (по ходу или против хода поезда) пассажир светит фонариком.
Замедление времени на высоких скоростях
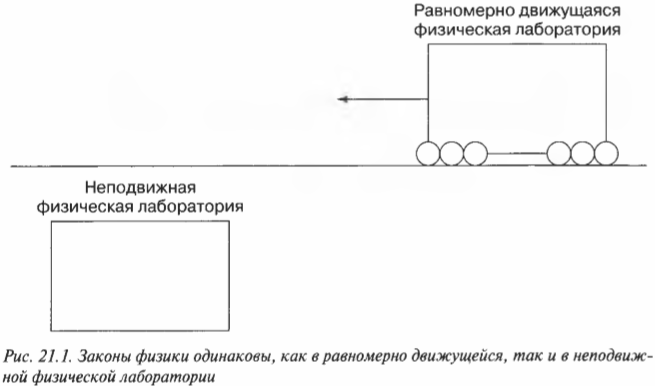
Представьте себе, что вы любуетесь звездным небом, а тут мимо вас “с ветерком” проносится ракета с астронавтом (рис. 21.2). Как утверждает специальная теория относительности Эйнштейна, события на космическом корабле происходят медленнее. Иначе говоря, для неподвижного наблюдателя время течет более быстро, чем время тех же событий, измеряемое астронавтом. Другими словами, наблюдателю на Земле кажется, что время замедляется, или “растягивается”.
Чтобы понять, как это может быть, посмотрите на схему А на рис. 21.2. На ней показаны специальные часы, в которых происходит периодическое отражение луча света от двух зеркал, которые вмонтированы во внутренние стенки ракеты на расстоянии \( D \) друг от друга. Астронавт может измерять время в интервалах, за которые свет проходит от одного зеркала другому. Но с вашей точки зрения, время ведет себя по-другому. Вы видите, как ракета проносится мимо вас, поэтому свету надо преодолеть не только расстояние \( D \) — ему надо также “учесть” дополнительное расстояние, проходимое ракетой в горизонтальном направлении.
Космические путешественники стареют медленнее
Те, кто путешествуют в космосе с околосветовыми скоростями, стареют заметно медленнее тех, кто остался на Земле. Только не говорите об этом своим богатым родственницам, одержимым погоней за красотой. Понаблюдаем за астронавтом, который движется со скоростью 0,99с, где \( c \) — это скорость света. Пусть для астронавта промежутки между очередными сигналами часов равны 1,00 секунде. Однако, согласно теории относительности, каждая секунда, прошедшая на ракете и измеренная астронавтом, по измерениям неподвижного наблюдателя на Земле равна 7,09 секундам.
Это явление имеет место даже при меньших скоростях. Рассмотрим реактивный самолет, который летит со скоростью 840 км/ч. Впрочем, скорость само- лета настолько мала по сравнению со скоростью света, что релятивистский (т.е. относящийся к теории относительности) эффект практически незаметен, и путешествие должно продолжаться около 100000 лет, чтобы часы неподвижного наблюдателя и часы пилота стали показывать разницу в 1 секунду. Физики провели этот эксперимент с реактивными самолетами и сверхчувствительными цезиевыми атомными часами, способными измерять время до 1,0·10-9 секунд. Полученные ими результаты очень точно соответствовали предсказаниям специальной теории относительности.
Уменьшение длины при высоких скоростях
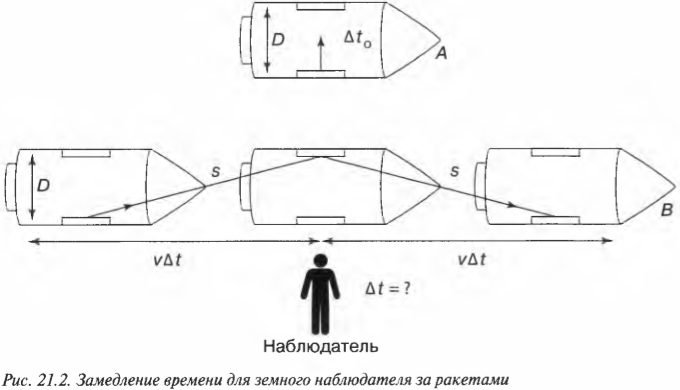
Оказывается, не только события на космических кораблях происходят медленнее (см. предыдущий раздел), но сама длина корабля меняется! Действительно, длина движущегося космического корабля, согласно измерениям на Земле, будет отличаться от его длины в состоянии покоя, согласно измерениям астронавта на корабле (рис. 21.3).
Длина объекта, полученная наблюдателем, который покоится относительно этого объекта, будет равна \( L_о \). А вот наблюдатель, движущийся относительно объекта со скоростью \( v \), получит меньшую длину этого объекта, равную \( L \). Иными словами, объект сжимается.
Обратите внимание, что сжатие происходит только в направлении движения. Как видно на рис. 21.3, ракета сжимается в направлении движения именно для неподвижного наблюдателя на Земле, а не для находящегося в ней астронавта.
E=mc2 : эквивалентность вещества и энергии
Самая знаменитая идея Эйнштейна — это утверждение об эквивалентности вещества и энергии, т.е. о том, что потерю или возрастание массы можно также считать потерей или возрастанием энергии. (Не могу удержаться от старой физической шутки: а как быть с тем, кто сидит на диете, ведь для него потеря массы как раз приводит к увеличению энергии?) Так какой формулой выражается эта идея Эйнштейна? \( E=mc^2 \)? На самом деле нет. Полученный им результат выражается следующей формулой:
Рассмотрим частный случай, когда преобразуемый в энергию объект покоится, т.е. \( v \) = 0. Тогда и только тогда действительно получаем знаменитую формулу \( E=mc^2 \).
Что означает знаменитая формула Эйнштейна? В некотором смысле можно считать, что масса — это “сконденсированная” энергия с коэффициентом преобразования килограммов в джоули, равным \( c^2 \), т.е. равным скорости света в квадрате.
Вещество плюс антивещество получается взрыв
Полное превращение массы в энергию можно получить, если соединить вещество и антивещество. Антивещество — это почти что стандартное вещество, но как бы с обратным знаком. В атомах антивещества вместо электронов имеются положительно заряженные позитроны, а вместо положительно заряженных протонов — отрицательно заряженные антипротоны. Фанаты научной фантастики могут считать антивещество той силой, которая работает в двигателях звездолета “Энтерпрайз” из телевизионного научно- фантастического сериала Звездный путь.
Но странное дело — антивещество действительно существует. Ученые вполне могут найти его во Вселенной, и Солнце практически все время его производит. Когда друг с другом встречаются стандартный атом водорода (электрон и протон) и атом антиводорода (позитрон и антипротон), они полностью, т.е. на 100% преобразуются в энергию. Что происходит с этой энергией? Она распространяется в виде высокоэнергетических фотонов (которые, прошу обратить внимание, могут передавать тепло в виде энергии излучения).
Не рассчитывайте на кончину Солнца
Мощность излучения Солнца равна 3,92·1026 Вт. Таким образом, за одну секунду оно излучает 3,92·1026 Дж энергии. Это значит, что Солнце теряет 4,36 миллиардов килограмм своей массы за секунду. Вот это да! Выходит, что каждую секунду Солнце “худеет” на 4,36 миллионов тонн вещества. Почему же молчат ученые-специалисты по Солнцу, ведь так Солнце может быстро исчезнуть? Однако не следует забывать, что масса Солнца равна около 1,99·1030 кг. Даже если каждую секунду оно теряет 4,36·109 кг своей массы, то Солнца все равно хватит на весьма долгое время. А на какое именно время? При условии, что единственный действующий на Солнце физический механизм — это превращение массы в излучение, наше светило продержится 1,99·1030/4,36·109 = 4,56·1020 с, т.е. примерно 1,44·1013 лет, или 144 миллиарда веков.
Солнце «излучает массу»
Большинство энергии, получаемой нами от Солнца, — это результат синтеза одних атомных ядер в другие. Каждую секунду Солнце излучает очень много света, и по этой причине оно в процессе излучения действительно теряет массу. И хотя наше светило теряет массу, преобразуемую в энергию излучения, все равно бояться нечего: то, что еще остается на Солнце, намного превышает то, что с него ушло.
Скорость света превысить нельзя
Если не принимать в расчет сериал Звездный путь и другие научно-фантастические сериалы и книги, то невозможно двигаться со скоростью, большей скорости света. Она является одинаковой во всех инерциальных системах отсчета (см. первый раздел этой главы), даже если видимый свет идет из инерциальной системы отсчета, которая движется прямо на вас. Согласно специальной теории относительности, общая энергия объекта выражается следующей формулой:
Для покоящегося объекта \( E_{покоя}=mc^2 \). Таким образом, релятивистская формула кинетической энергии для покоящегося объекта массой \( m \) должна иметь следующий вид:
Обратите внимание, что, когда скорость объекта возрастает, значение выражения в скобках становится все больше и больше, стремясь к бесконечности. Таким образом, если скорость объекта \( v \) бесконечно близко приближается к величине \( c \), то кинетическая энергия объекта становится почти бесконечной. Поэтому здесь, как это ни печально, научная фантастика терпит неудачу. И хотя для космических ракет характеристика “кинетическая энергия приближается к бесконечности” звучит впечатляюще, но в действительности это означает, что такой разгон до такой скорости осуществить нельзя. А если можно, то только вопреки специальной теории относительности.
Ньютон до сих пор прав
А что же законы Ньютона после всех этих разговоров об Эйнштейне? Как насчет старых добрых формул импульса и кинетической энергии? Так вот, все эти формулы до сих пор верны, но только при малых скоростях. Посмотрите на релятивистскую формулу импульса (более подробно об импульсе можно узнать в главе 9):
где \( p \), \( m \) и \( v \) — это соответственно импульс, масса и скорость. Обратите внимание на такую часть формулы:
Разницу, обусловленную этим множителем, можно заметить, лишь начав приближаться к скорости света. Дело в том, что он меняет значение формулы на 1% лишь тогда, когда скорость достигает величины, примерно равной 4,2·107 м/сек, что для эпохи Ньютона являлось довольно большой величиной. А при меньших скоростях релятивистским множителем можно пренебречь, получив таким образом:
Ньютон был бы вполне доволен этим результатом.
А как насчет формулы кинетической энергии (см. главу 8)? Вот как эта формула выглядит в релятивистском виде:
где \( K \) – это кинетическая энергия. Посмотрите на эту часть формулы:
Ее можно расписать в виде следующего ряда (разложение функции в ряд подробно изучается в курсе математического анализа):
Когда отношение \( \frac{v^2}{c^2} \) значительно меньше 1, то последнее равенство можно записать следующим образом:
Подставив правую часть равенства в релятивистскую формулу кинетической энергии, вы получите — догадались что? “Старый добрый” нерелятивистский вариант этой формулы (см. главу 8):
Как видите, законы Ньютона не повержены в прах, даже если речь идет о теории относительности. Механика Ньютона успешно применяется до сих пор для описания движений, скорость которых значительно меньше скорости света с. (Релятивистские эффекты начинают заметно проявляться, когда скорость составляет несколько процентов от скорости света. Исаак Ньютон жил еще во времена конно-гужевого транспорта и кабриолетов и потому никогда не наблюдал релятивистских эффектов.)






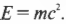
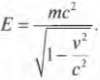
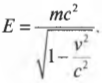
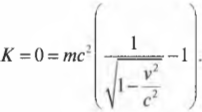
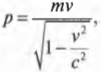
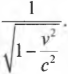
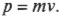
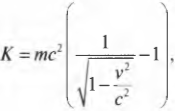
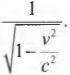
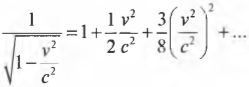
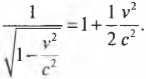
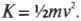
Добавить комментарий