Глава 18. Намагничиваемся: притягиваемся и отталкиваемся

В этой главе…
- Движемся сквозь магнитное поле
- Ловим движущиеся заряды
- Определяем силы, вызванные магнитными полями
- Изучаем поведение заряженных частиц в магнитном поле
- Путешествуем вместе с током в магнитных полях
- Создаем однородное магнитное поле с помощью соленоидов
Сильная связь между электричеством и магнетизмом наблюдается как при движении зарядов, создающих магнитное поле (как в электромагнитах и электродвигателях), так и при движении магнитов, создающих электрическое поле (как в электрических генераторах). Даже электроны, мчась по своим орбитам в атомах физического тела, генерируют магнитные поля. Эта глава посвящена магнетизму и его свойствам. Она начинается с описания свойств постоянных магнитов, затем продолжается рассказом о силах, возникающих под влиянием магнитного поля, и о том, что происходит с зарядами в этом поле.
Управление спутниками, которым нужна постоянная ориентация на звезды, Луну или на земные объекты, часто выполняется с помощью магнитной стрелки, которая управляется не реактивными двигателями, а магнитным полем Земли. Магнетизм и в космосе — сила!
Содержание
- Ищем источник магнетизма
- Воздействуем на движущийся заряд
- Вычисляем величину магнитной силы
- Движение по орбитам: заряженные частицы в магнитных полях
- Тяни-толкай на основе электрических токов
- Определяем магнитное поле провода с током
- Вычисляя магнитное поле в центре контура
- Создаем однородное магнитное поле с помощью соленоида
Ищем источник магнетизма
Если вы когда-то держали в руке два магнита, то знаете, что между ними могут возникнуть силы притяжения или отталкивания. Эти силы являются результатом действия магнитных полей, созданных на микроскопическом уровне.
В физических телах атомы генерируют крошечные магнитные поля, которые имеют беспорядочную ориентацию. Поэтому все эти поля нейтрализуют друг друга. Однако в некоторых веществах, таких как железо, атомы можно ориентировать таким образом, чтобы значительная часть их крохотных магнитных полей указывала в одном и том же направлении. В результате железо способно создать большое (макроскопическое) магнитное поле. Если тело способно создавать магнитное поле без внешнего воздействия, то оно называется постоянным магнитом. Два таких магнита показаны на рис. 18.1. Как видите, каждое из них создает силу, действующую на другой магнит.
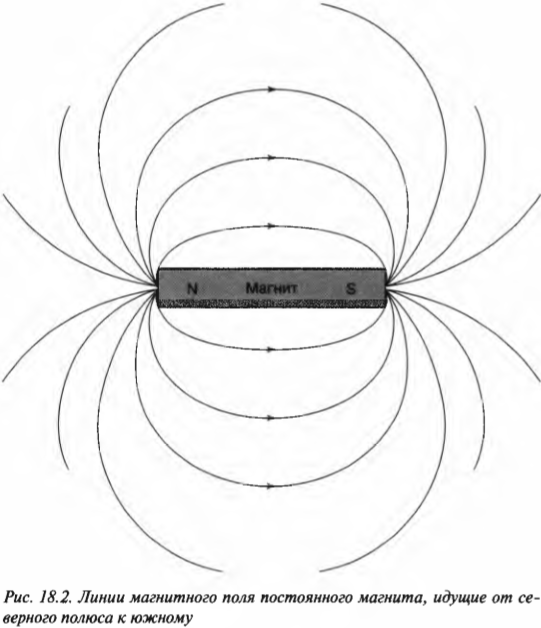
Магнетизм похож на электричество тем, что характеризуется положительными и отрицательными признаками в виде магнитных полюсов. Подобно тому, как линии электрических полей идут от положительных зарядов к отрицательным, так и линии магнитных полей идут от одного полюса к другому. В магнетизме полюса разного знака называются северным и южным.
Имена полюсов возникли в связи с использованием постоянных магнитов в компасах, где северный полюс ориентирован в северном направлении магнитного поля Земли.
Линии магнитного поля идут от северного полюса к южному, как показано на рис. 18.2 на примере постоянного магнита.
Воздействуем на движущийся заряд
Магниты влияют на электрический ток: они создают силу, которая действует на движущиеся в нем электрические заряды. Однако электрические заряды должны двигаться, иначе не будет силы, действующей на них со стороны магнитного поля.
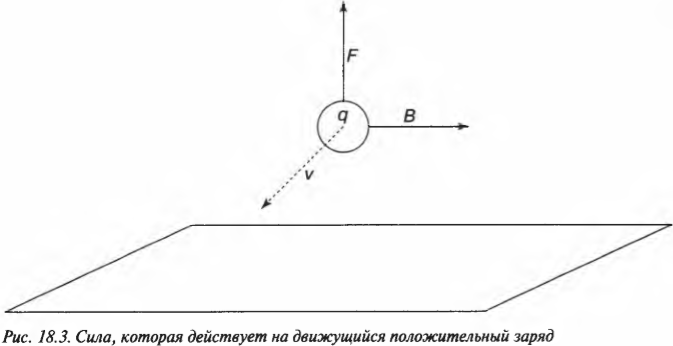
Как это происходит, показано на рис. 18.3, где на заряд, движущийся со скоростью \( \mathbf{v} \), через магнитное поле, показанное на рисунке вектором магнитной индукции \( \mathbf{B} \), действует сила со стороны этого магнитного поля. (Подробнее о векторах можно узнать в главе 4.)
(Магнитное поле в точке пространства определяется такой векторной величиной, как магнитная индукция \( \mathbf{B} \) в этой точке. Она играет ту же роль в магнетизме, что и напряженность электрического поля \( \mathbf{E} \) в электростатике. Направление поля в точке — это направление в ней вектора магнитной индукции, указываемое стрелкой компаса в этой точке. Линии магнитного поля — это линии, проведенные так, что касательные к ним в каждой точке указывают направление магнитной индукции в этой точке. — Примеч. ред.)
Магнитное поле создает силу, которая действует на движущийся заряд. Куда же направлена эта сила? Ответ можно увидеть на рис. 18.3, как и правило правой руки, с помощью которого вы сможете самостоятельно отвечать на этот вопрос.
Правило правой руки относится к движущимся зарядам; ниже перечислены два его варианта — выбирайте из них тот, какой вам покажется более легким.
Вариант 1. Если все пальцы правой руки, кроме большого, поместить вдоль магнитного поля (на рис. 18.3 оно показано вектором \( \mathbf{B} \)), а большой палец этой руки — в направлении скорости \( \mathbf{v} \) заряда, то сила, действующая на положительный заряд, должна выходить из ладони. Если заряд отрицательный, то сила направлена в противоположную сторону.
Вариант 2. Пальцы правой руки, кроме большого, поместите в направлении скорости v заряда, а затем сближайте их с ладонью, поворачивая на минимально возможный угол (меньший, чем 180°), пока они не будут указывать в направлении магнитного поля \( \mathbf{B} \). Тогда большой палец правой руки будет указывать в направлении действия силы.
Эти правила, возможно, напомнят вам сведения о моменте силы (его иногда называют вращающим моментом) (глава 10). Дело в том, что вектор силы выходит из плоскости, образованной векторами \( \mathbf{v} \) и \( \mathbf{B} \).
(В русскоязычной литературе принято использовать правило левой руки: если положить левую руку на проводник так, чтобы четыре пальца указывали направление тока, а линии магнитной индукции входили в ладонь, то отогнутый большой палец укажет направление силы, действующей на проводник. — Примеч. ред.)
Пользуясь любым из этих правил, вы сможете найти направление, в котором сила действует на движущийся заряд. Но насколько велика эта сила?
Вычисляем величину магнитной силы
Количественную величину магнитной силы полезно знать при работе с магнитами, например, для определения силы (в ньютонах), которая действует на заряженную частицу, движущуюся в магнитном поле.
Дело в том, что эта сила пропорциональна как величине заряда, так и величине магнитной индукции. Кроме того, эта сила пропорциональна компоненту скорости, перпендикулярному вектору магнитной индукции. Другими словами, на заряд, движущийся вдоль направления магнитной индукции (или, как еще говорят, вдоль магнитного поля), никакая сила не действует. А на заряд, движущийся под прямым углом к магнитному полю, действует максимальная сила. Сведя эту информацию воедино, становится понятен смысл следующей формулы для величины силы, которая действует со стороны магнитного поля \( \mathbf{B} \) на заряд \( q \), движущийся со скоростью \( \mathbf{v} \) под углом \( \theta \) между векторами \( \mathbf{v} \) и \( \mathbf{B} \):
На самом деле в физике определяется не сила магнитного поля через магнитную индукцию, а магнитная индукция посредством той силы, с которой она действует на положительный пробный заряд, то есть:
В системе СИ (см. главу 2) единицей магнитной индукции является тесла (Тл). А в системе СГС (см. также главу 2) такой единицей является гаусс (Гс). Они связаны друг с другом следующим образом: 1 Гс = 10-4 Тл.
Рассмотрим электрон в магнитном поле с индукцией в 12 Тс (громадная величина, учитывая, что индукция магнитного поля Земли на ее поверхности примерно равна 0,6 гаусса, или 6,0·10-5 Тс). Какая сила действует на электрон, если он несется со скоростью 1,0·106 м/с в направлении, перпендикулярном полю? Величина этой силы выражается формулой:
и нам остается только подставить в нее числа:
Сила, действующая на этот электрон, равна 1,92·10-12 Н и выглядит не такой уж большой. Однако следует напомнить, что электрон имеет слишком малую массу 9,11·10-31 кг. Каким будет ускорение этого электрона? Используя известную формулу второго закона Ньютона (согласно которой ускорение объекта равно отношению действующей на него силы и массы), получим:
Получается просто колоссальная даже для электрона величина, примерно равная 215 000 000 000 000 000 \( g \), где \( g \) — это ускорение свободного падения в поле силы тяжести на поверхности Земли. С другой стороны, если бы этот электрон двигался вдоль магнитного поля, то никакие магнитные силы на него не действовали бы.
Движение по орбитам: заряженные частицы в магнитных полях
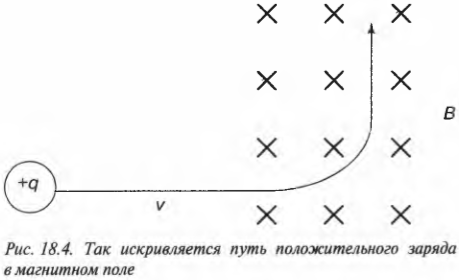
Положительный заряд, помещенный в электрическое поле плоского конденсатора (см. главу 17), будет двигаться в направлении, противоположном направлению линий поля. Дело в том, что эти линии выходят из зарядов, которые расположены на положительной пластине, отталкивающей положительный заряд. Впрочем, когда речь идет о магнитном поле, то здесь все иначе из-за того, что магнитное поле не действует на параллельно движущиеся заряды. На рис. 18.4 показан путь положительного заряда, движущегося перпендикулярно к силовым линиям магнитного поля.
Заметили на рисунке крестики? Так в физике принято обозначать направление линий магнитного поля, когда они направлены от читателя и входят в страницу вдоль перпендикуляра к ней. Подразумевается, что крестики обозначают концы воображаемых векторных стрелок, которые именно так выглядят сзади. Положительный заряд движется по прямой, пока не войдет в магнитное поле и не начнет подвергаться силовому воздействию. Как можно проверить с помощью правила правой (или левой) руки, сила магнитного поля будет направлена вверх и, как показано на рисунке, будет делать путь заряженной частицы изогнутым.
Магнитные поля не выполняют работу…
Как известно, на заряженную частицу в магнитном поле действует сила, но какую работу проделывает магнитное поле над этим зарядом? Да, хороший вопрос.
Когда заряд движется в электрическом поле, оно выполняет с ним работу, благодаря которой и вводится понятие разности потенциалов, т.е. проделанной над зарядом работы \( W \), деленной на величину этого заряда \( q \) (иными словами, работы, проделанной над одним кулоном):
А какую работу проделывает над зарядом магнитное поле? Ее можно вычислить таким образом (как показано в главе 6):
где \( s \) — это расстояние. Так… Вы уже заметили? Здесь \( \theta \) — это угол между силой и направлением, вдоль которого она действует. Но, согласно правилу правой руки, для зарядов в магнитном поле угол \( \theta \) всегда равен 90°, a cos90° = 0, т.е. работа, которая выполняется магнитным полем над движущимся зарядом, равна нулю.
Эта особенность является еще одним важным отличием электрического и магнитного полей. Электрическое поле всегда выполняет работу над движущимся зарядом, а магнитное поле — никогда, и потому оно не может изменить его кинетическую энергию.
…но влияют на движущиеся заряженные частицы
Несмотря на нежелание работать с движущейся заряженной частицей, магнитное поле может изменить направление движения этой частицы (что оно и делает). На самом деле, если направление движения заряда можно свободно менять, то магнитное поле будет всегда это делать, так как сила, действующая на заряд, всегда направлена перпендикулярно его движению.
Не припомните какой-то другой вид движения, направление которого всегда перпендикулярно приложенной силе? Ну конечно, это вращательное движение, о котором говорилось в главе 7. Такое движение заряда можно увидеть на рис. 18.4, когда он проходит через магнитное поле. Так как магнитные поля действуют на заряд перпендикулярно направлению его движения, то движение зарядов, не выходящих за пределы магнитного поля, будет вращательным.
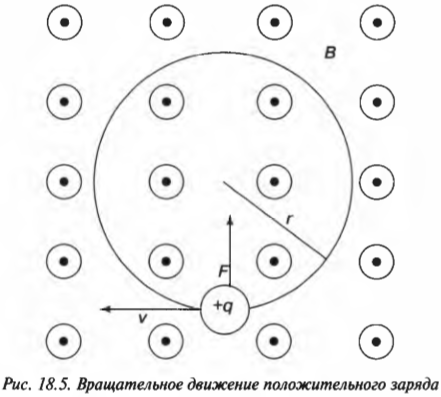
Посмотрите на рис. 18.5, где положительный заряд движется в магнитном поле влево. Поле \( \mathbf{B} \) направлено вверх от плоскости страницы к читателю. Откуда это известно? Видите все эти точки внутри кружочков? Так же, как крестик обозначает стрелку вектора, направленную от читателя, так и точка внутри кружочка обозначает стрелку, направленную к читателю. Поэтому сейчас поле \( \mathbf{B} \) направлено вверх, т.е. от страницы к читателю.
Итак, поле \( \mathbf{B} \) направлено от страницы к читателю, а положительный заряд движется влево. Используя правило правой (или левой) руки, можно сказать, что результирующая сила направлена вверх (подробнее о правиле правой руки рассказывается выше в этой главе). Под действием силы, направленной вверх, заряд также движется вверх. Но так как благодаря действию магнитного поля сила всегда перпендикулярна направлению движения, то она также меняет свое направление. Вот формула величины силы:
Так как в данном случае вектор скорости \( \mathbf{v} \) перпендикулярен вектору магнитной индукции \( \mathbf{B} \), то \( \theta \) = 90°, или \( \sin\!\theta \) = 1, а это означает, что:
Так как сила всегда перпендикулярна направлению движения, то таким образом возникает движение по кругу. Другими словами, она является ничем иным, как центростремительной силой, нужной для обеспечения вращательного движения (глава 7).
где \( m \) — это масса частицы, а \( r \) — радиус орбиты вращательного движения. Таким образом, получаем:
Отсюда легко найти радиус орбиты вращательного движения:
Таким образом, можно вычислить радиус орбиты вращательного движения заряда \( q \) массой \( m \), движущегося со скоростью \( \mathbf{v} \) в магнитном поле с индукцией \( \mathbf{B} \). Чем магнитная индукция сильнее, тем радиус меньше. А чем быстрее движется заряд и чем больше его масса, тем радиус больше.
Тяни-толкай на основе электрических токов
Информация, полученная в этой главе до сих пор, просто удивительна, но как часто нам приходится иметь дело с движущимися зарядами? Возможно, кому-то и приходится работать с электронами, движущимися в вакууме, но большинство из нас сталкивается практически ежедневно не с одиночными движущимися зарядами, а с их группами, т.е. с электрическим током.
Сила, действующая на ток
Посмотрите на формулу силы, действующей на движущийся заряд:
где \( q \) — заряд, \( v \) — скорость, а \( B \) — значение магнитной индукции. Обладая полученными выше сведениями, нетрудно преобразовать эту формулу, одновременно поделив и умножив ее на \( t \) так, чтобы сама формула не изменилась:
Обратите внимание, что \( q/t \) — это заряд, проходящий через определенную точку за единицу времени, т.е. величина, известная под другим именем—электрический ток. Ну а \( vt \) — это всего лишь путь, который заряды проходят за время \( t \), поэтому прежнюю формулу можно переписать так:
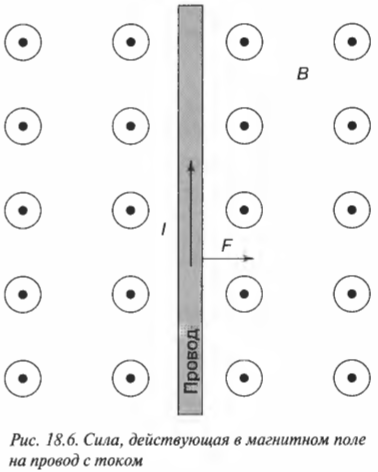
Это сила, действующая на провод длины \( L \), через который проходит ток силой \( I \) в магнитном поле с индукцией \( \mathbf{B} \) и расположенный к этому полю под углом \( \theta \).
На рис. 18.6 показан провод, несущий ток силой \( I \) в магнитном поле с индукцией \( \mathbf{B} \) и расположенный к этому полю под углом 90°. Поскольку в физике за направление тока принято направление движения положительного заряда, то легко найти силу, действующую на провод. Пусть \( I \) = 2,0 А и \( B \) = 10 Тл. Какая сила будет действовать на провод длиной 1 м? Так как провод перпендикулярен к магнитному полю, то:
Силу, действующую на единицу длины, можно найти по формуле:
Подставляя в нее численные значения, получим:
Двадцать ньютонов на метр длины — это довольно заметная величина.
Момент силы, действующий на проводник с током
В электромоторах обычно используются постоянные магниты, а поля, создаваемые этими магнитами, пронизывают электрические катушки. Эти катушки могут вращаться благодаря тому, что приложенная к ним сила создает вращающий момент силы (см. главу 10). Как происходит это вращение, можно увидеть на рис. 18.7.
На схеме А показан контур с током в магнитном поле, которое создает действующие на контур силы, подробно показанные на схеме Б того же рисунка. Эти силы создают вокруг центральной оси два момента силы. Как показано на указанной схеме Б, плечо силы (см. главу 11) каждого момента силы выражается следующей формулой:
где \( d \) — это ширина контура. Каждый момент силы — это сила \( F \), умноженная на плечо силы, а сама сила \( F \) равна произведению силы тока \( I \) на длину контура \( L \) и на величину магнитной индукции \( B \). Так как имеется два момента силы, соответствующие двум сторонам контура, то получится общий момент сил \( M \):
Получается интересный результат, так как произведение \( dL \) равно площади контура. Таким образом, для контура с площадью поперечного сечения \( A \) и углом \( \theta \). показанным на схеме Б, получим следующую формулу вращающего момента силы:
Впрочем, как правило, катушки содержат большое количество витков провода, т.е. контуров. Например, если катушка состоит из \( N \) витков провода, то для получения общего вращающего момента силы надо вращающий момент силы в одном витке (контуре) умножить на их количество \( N \):
Теперь можно найти общий вращающий момент силы проволочной катушки, состоящей из \( N \) витков, через каждый из которых проходит ток силой \( I \), имеет площадь \( A \) поперечного сечения и расположен к магнитному полю с индукцией \( B \) под углом \( \theta \). Ну наконец-то!
Рассмотрим следующую физическую задачу: найти максимально возможный вращающий момент силы, который будет испытывать в магнитном поле катушка из \( N \) витков. Чтобы найти этот момент, нужно выяснить, когда принимает максимальное значение множитель \( \sin\!\theta \). Это возможно в случае, когда \( \theta \) = 90°, т.е. \( \sin\!\theta \) = 1. Итак, получаем формулу максимального вращающего момента силы:
Например, каков максимальный вращающий момент силы для катушки, состоящей из 2000 витков, через которую проходит ток силой 5 А, имеющей площадь поперечного сечения 1,0 м2 и находящейся в магнитном поле с индукцией в 10 Тл? Ответ получить довольно легко:
Итак, максимальный вращающий момент силы равен 1,0·105 Н·м. Он имеет такое большое значение, потому что используется катушка с большим количеством витков. А если ограничиться одним-единственным витком, то максимальный вращающий момент силы будет равен всего 50 Н·м. Вот почему вращающиеся части электромоторов имеют так много витков провода.
Определяем магнитное поле провода с током
Движущиеся электрические заряды не только реагируют на воздействие магнитных полей (например, меняют направление движения; см. раздел о движении заряженных частиц в магнитных полях), но и сами создают магнитные поля. Токи состоят из движущихся частиц с электрическим зарядом и поэтому являются удобным средством для создания магнитных полей.
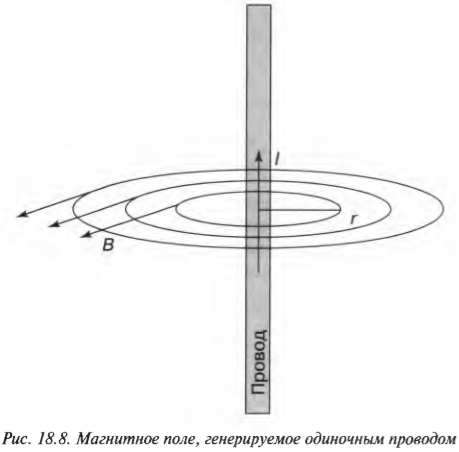
Попробуем определить магнитное поле, генерируемое с помощью одиночного провода с электрическим током (рис. 18.8). Обладая навыками определения магнитного поля от провода с током, можно определять магнитное поле, генерируемое сложной конфигурацией проводов с током. Для этого надо будет всего лишь разбить их на “отдельные” провода, а затем вычислить векторную сумму магнитных полей всех проводов.
Из опыта известно, что чем больше расстояние от провода, тем слабее создаваемое им магнитное поле. Оно уменьшается обратно пропорционально расстоянию \( r \) от центра провода:
Забавное происшествие с гаечным ключом, ставшее исследованием магнитного поля
Еще будучи студентом, я проводил научные исследования в Национальной магнитной лаборатории Массачусетского технологического института, вблизи очень толстых кабелей, по которым проходил ток с очень большой силой, более 1000 А. Однажды я споткнулся об один из таких кабелей и уронил рядом с ним гаечный ключ. Поднимая этот ключ, я почувствовал мощное магнитное поле, генерируемое кабелем. Перемещая гаечный ключ вокруг кабеля на разных расстояниях от него, я убедился, что магнитное поле действительно уменьшается обратно пропорционально расстоянию от центра провода и является фуговым, как меня учили, ‘Вот это да!” — подумал я тогда. Впрочем, профессор, с которым я работал, сказал, чтобы я прекратил заниматься ерундой и принимался за работу.
Кроме того, известно, что магнитное поле пропорционально силе тока \( I \): если она удваивается, то магнитная индукция тоже удваивается. Таким образом:
Исторически сложилось, что константа пропорциональности в этой формуле имеет вид \( \mu_0/2\pi \), т.е. итоговая формула магнитной индукции провода с электрическим током имеет вид:
где \( I \) — это сила тока, текущего по проводу, \( r \) — расстояние от центра провода, a \( \mu_0 \) — магнитная постоянная, равная 4π·10-7 N·A-2.
В какую сторону направлен вектор магнитной индукции для магнитного поля, созданного проводником с током? Чтобы это узнать, надо воспользоваться еще одним правилом правой руки. Если расположить большой палец этой руки по направлению тока, то остальные сжатые в кулак пальцы будут указывать круговое направление вектора магнитной индукции (см. рис. 18.8).
Пусть в проводе протекает ток силой 1000 А, а вы находитесь в 2 см от центра этого провода. Насколько большим будет магнитная индукция в этом месте? Как известно:
Тогда, подставив в эту формулу численные значения, получим:
Еще один пример. Пусть два параллельных провода расположены друг от друга на расстоянии \( r \) и по ним идет одинаковый ток силой \( I \). С какой силой на провод 1 действует провод 2? Как известно, сила, с которой магнитное поле с индукцией \( B \) действует на провод 1 с током силой \( I \), вычисляется по формуле:
Чему равно значение \( B \)? На проводе 1 индуцируется магнитное поле проводом 2, которое вычисляется по формуле:
Поэтому:
Используя правило правой руки, можно убедиться, что если ток по проводам идет в одну сторону, то силы от них направлены навстречу друг другу, т.е. они притягиваются. И наоборот, если ток по проводам идет в разные стороны, то их силы взаимодействия направлены в противоположные стороны, т.е. провода отталкиваются.
Вычисляя магнитное поле в центре контура
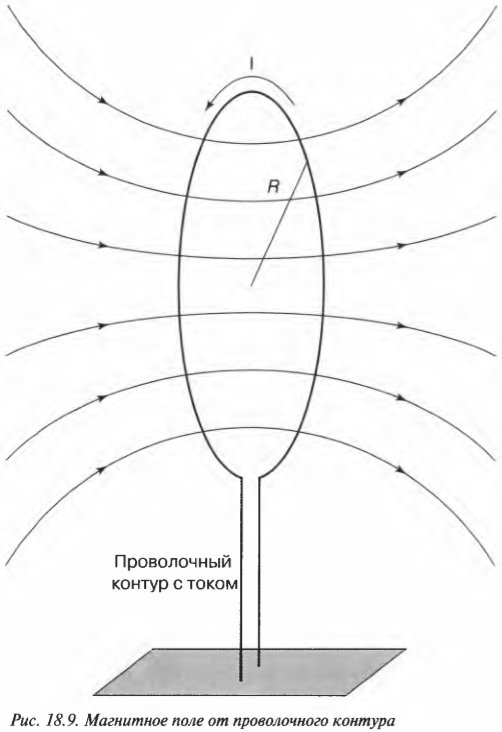
Представьте себе, что на совещании группы разработчиков потребовалась ваша помощь. Взгляните на странное устройство, показанное на рис. 18.9. Вы видели что-либо подобное раньше?
“Конечно, — скажете вы. — Это ведь обычный контур с током.”
“Отлично, — ответят ваши коллеги. — Нам нужно вычислить магнитную индукцию в самом центре контура.”
“В самом центре?”
“Вот именно.”
“А мне заплатят?”
“Конечно.”
“Ладно, — скажете вы. — Магнитная индукция в самом центре контура с током определяется следующей формулой:
где \( N \) — количество витков контура, \( I \) — сила тока в нем, a \( R \) — радиус контура.”
А куда направлено магнитное поле? И на этот вопрос мы уже готовы дать ответ. Пусть все пальцы правой руки, кроме большого, сжимаются в кулак по направлению тока, тогда большой палец укажет направление вектора магнитной индукции \( \mathbf{B} \) для магнитного поля, генерируемого контуром с током.
Пусть контур содержит не один виток, а 2000 витков, ток в нем равен 10 А, а радиус контура равен 10 см. Какова величина магнитной индукции в центре контура? Достаточно просто подставить численные значения в известную формулу:
Итак, контур из 2000 витков создает магнитное поле с магнитной индукцией 0,13 Тл.
Создаем однородное магнитное поле с помощью соленоида
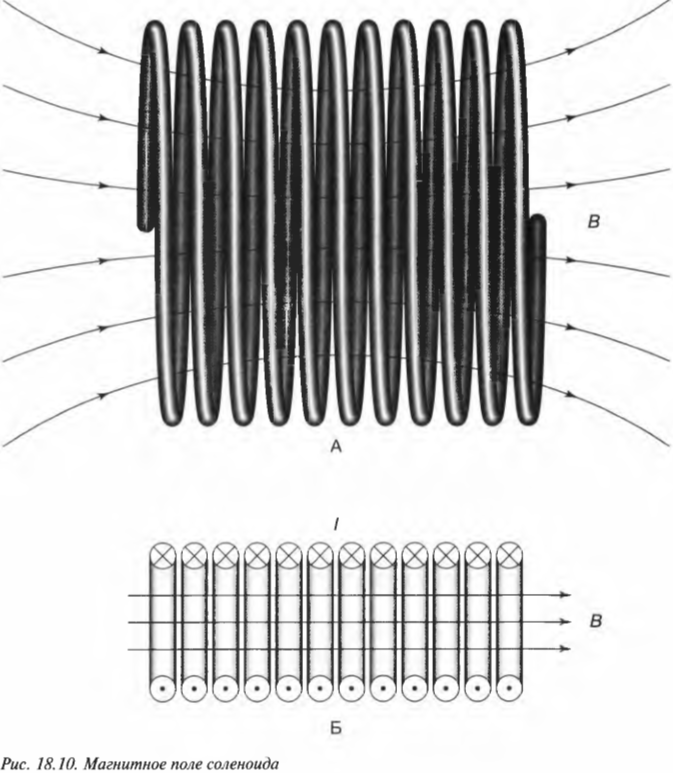
Как создать однородное магнитное поле, т.е. такое же, как однородное электрическое поле, образуемое плоскими конденсаторами (см. главу 16)? Для этого нужно соединить друг с другом множество контуров тока, как показано на рис. 18.10.
Если расположить множество контуров друг за другом (как показано на схеме А), то внутри тоннеля, получившегося из этих контуров, образуется однородное магнитное поле (как показано на схеме Б).
Эта новая конструкция, создающая однородное магнитное поле, называется соленоидом. Итак, соленоид — это просто множество контуров, расположенных рядом друг с другом, благодаря чему и получается однородное магнитное поле.
Предположим, что для выполнения эксперимента надо создать однородное магнитное поле с индукцией в 1 Тл, используя соленоид с 100 тыс. витков на метр. Какой должна быть сила тока? Просто подставьте числа:
Какова же величина магнитной индукции поля, генерируемого соленоидом? Если длина соленоида гораздо больше его радиуса, то магнитная индукция поля, генерируемого соленоидом, вычисляется по следующей формуле:
где \( n \) — количество витков на единицу длины соленоида, \( I \) — сила тока в каждом витке. Чтобы определить направление вектора магнитной индукции поля, генерируемого соленоидом, следует использовать правило правой руки для контура с током (см. предыдущий раздел).
Итак, для получения нужного магнитного поля потребуется ток силой примерно 8 А.







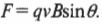
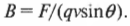
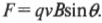
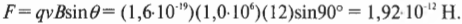
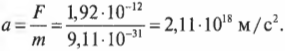
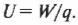
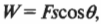
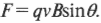
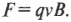
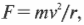
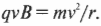
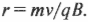
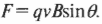
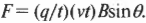
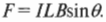
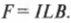
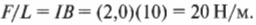
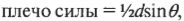
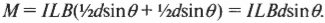
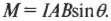
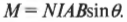
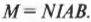
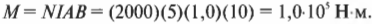
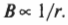
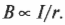
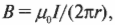
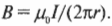
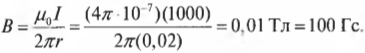
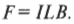
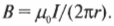
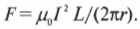
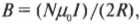
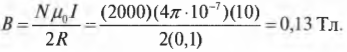
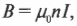
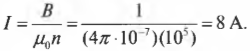
Добавить комментарий