Глава 17. Летим вслед за электронами по проводам

В этой главе…
- Исследуем движение электронов и электрический ток
- Вычисляем напряжение и сопротивление по закону Ома
- Оцениваем мощность электрического тока
- Разбираемся с параллельными и последовательными цепями
- Знакомимся с правилами Кирхгофа
Статическое электричество возникает при избытке либо недостатке электронов, т.е. когда имеются отрицательно или положительно заряженные тела. А в привычном электричестве, т.е. в текущем по проводам электрическом токе, избыточного заряда нет, и, следовательно, нет и общего заряда. Есть лишь напряжение, подобное тому, которое создается батарейкой или настенной розеткой. Оно создается в проводах электрическим полем, в ответ на которое возникает движение электронов — электрический ток. (Более подробно о напряжении рассказывается в главе 16.)
Эта глава посвящена электронам, т.е. заряженным частицам, движущимся в электрических контурах, с которыми вы уже знакомы. В главе 16 рассказывается о статическом, а в этой — только о динамическом проявлении электричества. Здесь описываются сходства и различия между ними, носители и источники электрического тока, закон Ома, мощности электрического тока и, наконец, электрические контуры и их элементы.
Содержание
Марширующие электроны: ток
Электрический ток возникает при направленном движении электронов. Но как заставить их двигаться именно так, чтобы получился электрический ток? Ответ: нужно создать и поддерживать электродвижущую силу, или э.д.с. Э.д.с. обеспечивает разность потенциалов (напряжение), благодаря которой электроны чувствуют силовое воздействие.
Итак, чем именно создается э.д.с.? Батарейкой? Или настенной розеткой? Э.д.с. — это то, что дает напряжение, ведь напряжение — это все, что нужно для создания электрического поля в проводе, которое заставляет электроны двигаться. (В главе 16 говорится, что электрическое поле характеризуется своей напряженностью \( E \), которая равна отношению силы \( F \) и заряда \( q \): \( Е = F/q \).)
В физике величина электрического тока (сила тока) обозначается буквой \( I \) и измеряется в амперах (А).
Знакомимся с силой тока
Как правильно определить силу тока? Это величина заряда, проходящего через некоторую часть контура за некоторое время. А вот то же самое определение, но в виде формулы:
где \( q \) и \( t \) — это соответственно электрический заряд и время. Если за 1 с через контур проходит заряд в 1 Кл, то величина электрического тока равна 1 А.
Вычисляем силу тока, идущего через батарейку
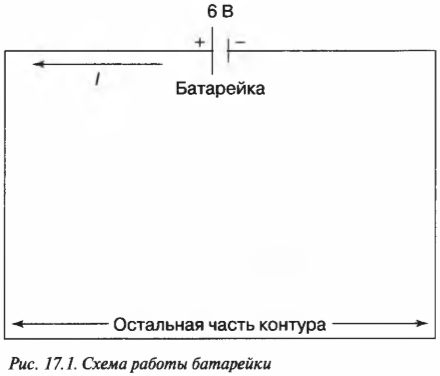
Зная величину заряда в контуре с батарейкой и время, можно вычислить силу тока, идущего через батарейку: \( I=q/t \). Посмотрите на рис. 17.1; две вертикальные черты, расположенные сверху, означают батарейку. (Эти линии напоминают о разных металлических пластинах в первых батарейках, которые подвергались воздействию химических веществ и соединялись вместе.)
Батарейка обеспечивает электродвижущую силу величиной 6 В, которая гонит ток по контуру. Если за 30 с по контуру проходит заряд 19 Кл, то чему равна сила тока?
В данном случае по контуру течет 0,633 ампера. Обратите внимание, что ток идет от положительной части батарейки, обозначаемой на значке батарейки более длинной чертой, к отрицательной части, обозначаемой на значке батарейки более короткой линией.
Полезно считать, что в цепи батарейка является ступенькой напряжения. Иначе говоря, батарейка как бы “поднимает” ток, поступающий в ее отрицательную часть (в случае рис. 17.1 на уровень 6 В), а затем электрический ток снова “спускается” и течет по контуру.
Хотя ток всегда изображается движущимся по контуру от положительного к отрицательному знаку батарейки, но в действительности электроны движутся в противоположном направлении. Почему возникло такое различие? Причина здесь историческая: первые исследователи думали, что по контуру текут именно положительные заряды, но на самом деле все происходит наоборот. Впрочем, это не проблема, если вы будете придерживаться единообразия и всегда считать, что ток выходит с положительного конца батарейки.
Оцениваем сопротивление: закон Ома
Сопротивление — это величина, которая связывает приложенное напряжение с созданной им силой тока. Вот как выглядит формула, которая связывает напряжение, силу тока и сопротивление:
где \( U \), \( I \) и \( R \) — это соответственно напряжение, сила тока и сопротивление. Сопротивление измеряется в омах (Ом), 1 Ом = 1 В/1 А. Таким образом, прикладывая напряжение \( U \) на участке цепи с некоторым сопротивлением \( R \), получим силу тока \( I \). Это и есть закон Ома, названный так по фамилии своего открывателя Георга Симона Ома (сделавшего свое открытие в XIX веке).
Вычисляем силу тока
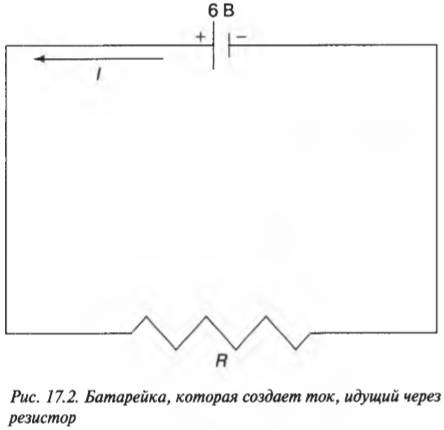
С помощью закона Ома можно найти силу тока, идущего от положительной к отрицательной клемме батарейки. Посмотрите на цепь, показанную на рис. 17.2, где батарейка с напряжением 6 В создает электрический ток, идущий через резистор \( R \) с сопротивлением 2 Ом.
Из закона Ома следует, что:
Подстановка числовых значений дает:
Итак, ток силой 3 А течет по контуру против часовой стрелки.
Проверка удельного сопротивления
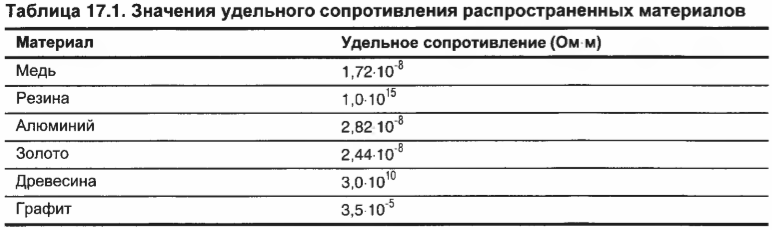
При изучении электричества часто приходится иметь дело с величиной \( \rho \) называемой удельным сопротивлением, т.е. сопротивлением на единицу длины и площади, и измеряемой в Ом·м. Зная силу тока через определенный материал, можно с помощью удельного сопротивления материала узнать его сопротивление. Физики вычислили значения удельного сопротивления многих распространенных материалов; некоторые из этих значений перечислены в табл. 17.1.
Сопротивление материала \( R \) можно найти, умножив его удельное сопротивление \( \rho \) на его длину \( L \) (чем она больше, тем большее сопротивление вызывает) и поделив на площадь \( A \) поперечного сечения этого материала (чем больше площадь, которую должен пересекать ток, тем сопротивление меньше):
Измеряем мощность: ватт
Некоторые предметы домашнего обихода, например, лампочки накаливания или сушилки для волос, используют электроэнергию. Мощность таких электроприборов измеряется в ваттах (Вт). Как определить ее величину? Работа по перемещению заряда \( q \) по цепи равна \( qU \), где \( U \) — это электродвижущая сила. Если поделить эту работу на время ее выполнения, получится мощность:
Впрочем, заряд \( q \), деленный на время \( t \), равняется силе тока \( I \), таким образом:
Мощность, которая обеспечивается в цепи источником э.д.с., в частности батарейкой, вычисляется по формуле \( P = IU \). Например, батарейка при 10 В создает в лампочке накаливания силу тока 0,5 А. Какова мощность этой лампочки? \( P = IU \), т.е. мощность равна 0,5·10 = 5 Вт. Впрочем, \( I = U/R \), поэтому мощность, обеспечиваемую в цепи определенным напряжением, можно вычислять несколькими способами:
От одного к другому: последовательные цепи
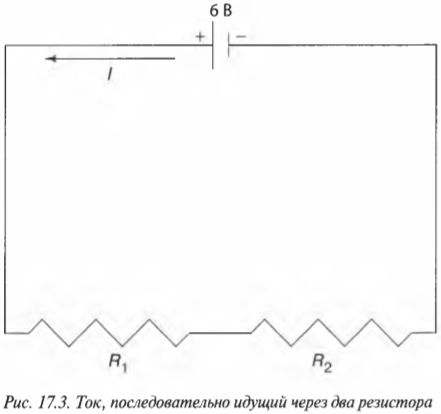
В предыдущих разделах этой главы говорилось о токе, идущем через один резистор; впрочем, как показано на рис. 17.3, в цепи может быть и два резистора.
Два резистора могут быть подключены последовательно, когда, перед тем как вернуться к источнику электродвижущей силы (см. первый раздел этой главы), ток в цепи течет сначала через один из них, а затем — через другой. Рассмотрим последовательное подключение двух резисторов с сопротивлениями \( R_1 \) и \( R_2 \), когда один и тот же ток, перед тем как вернуться к батарейке, должен пройти через оба резистора. Тогда общее сопротивление \( R \) должно равняться сумме этих двух сопротивлений:
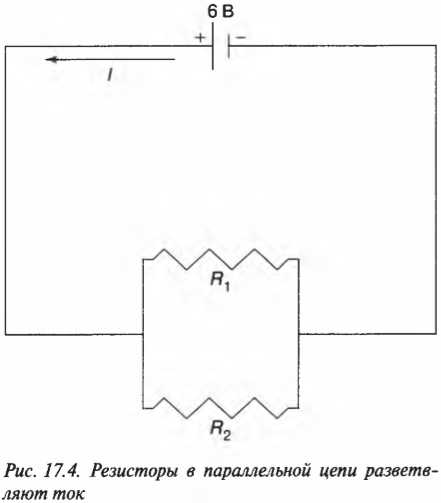
Итак, чтобы получить общее сопротивление двух последовательно соединенных резисторов, надо сложить их сопротивления \( R_1 \) и \( R_2 \). Например, если \( R_1 \) = 10 Ом и \( R_2 \) = 20 Ом, батарейка создает напряжение 6 В, то ток какой силы будет проходить через цепь? Общее сопротивление должно равняться 30 Ом, тогда:
Разделение тока: параллельные цепи
Если в одной и той же цепи имеется множество резисторов, то совсем не обязательно, чтобы у них было только последовательное соединение (см. предыдущий раздел), когда ток идет от одного резистора к другому. Два резистора \( R_1 \) и \( R_2 \) можно соединить таким образом, чтобы ток разветвлялся, как на рис. 17.4. Какая-то часть тока идет через первый резистор, а другая — через второй.
Резисторы на рис. 17.4 являются параллельными, т.е. на концах каждого из них одно и то же напряжение, но ток, идущий через эти резисторы, не обязательно одинаковый.
Напряжение на концах каждого из параллельных резисторов одинаково и равно 6 В, т.е. напряжению, создаваемому батарейкой. Этим и отличаются последовательно и параллельно соединенные резисторы. Через последовательно соединенные резисторы идет один и тот же ток. А когда резисторы соединены параллельно, на концах каждого из них одинаковое напряжение.
Итак, чему равно общее сопротивление резисторов \( R_1 \) и \( R_2 \) соединенных параллельно? Общая сила тока \( I \) — это сила тока, идущего через два резистора:
И поскольку \( I=U/R \) (см. выше раздел о законе Ома), то можно записать:
Дело в том, что при параллельном соединении \( U_1=U_2 \), поэтому если обозначить это общее напряжение как \( U \), то можно сказать, что:
Это равенство еще записывается как \( I=U/R \), и в итоге мы получаем:
Эта формула показывает, как надо вычислять общее сопротивление двух параллельно соединенных резисторов. Если говорить о произвольном количестве резисторов, то получится такой способ вычисления общего сопротивления:
Например, если на рис. 17.4 \( R_1 \) = 10 Ом и \( R_2 \) = 30 Ом, а напряжение батарейки составляет 6 В, то ток какой силы идет через эту цепь? Величина, обратная общему сопротивлению цепи, равна
Чтобы найти общее сопротивление при параллельном соединении, надо сложить величины, обратные значениям сопротивления, а затем взять величину, обратную полученному результату. Таким образом, общее сопротивление равно 30/4 Ом, т.е. сила тока равна 6/(30/4) = 0,8 А.
Создаем электрические цепи по правилам Кирхгофа
К сожалению, электрические цепи не всегда можно разбить на последовательные и параллельные составляющие, поэтому важную роль играют правила Кирхгофа, названные так в честь своего открывателя, Густава Кирхгофа. Эти два простых правила позволяют анализировать цепи самой разной сложности, поскольку представляют собой неизменные соотношения целостности, которые выполняются между токами и напряжениями на участках любой электрической цепи. (Для корректной формулировки этих правил в цепи выделяются узлы, т.е. точки соединения трех и более проводников, и контуры, т.е. замкнутые пути из проводников. — Примеч. ред.)
- Правило соединения. Общий ток, притекающий в любой узел цепи, должен равняться общему току, вытекающему из него.
- Правило контуров. В любом замкнутом контуре сети сумма увеличений потенциала (например, от батарейки) должна равняться сумме падений потенциала (например, от резистора). (Иначе говоря, суммарная э.д.с. равна суммарному напряжению. — Примеч. ред.)
Правило соединения достаточно легко понять: сила тока, входящего в любой узел, должна равняться силе тока, выходящего из этого узла. Ну а как насчет правила контуров, которое гласит, что в любом замкнутом контуре суммарное увеличение и суммарное падение потенциала должны быть равны? Правило контуров означает, что насколько движущиеся по контуру электроны “спускаются”, настолько они и “поднимаются”, и приходят туда, откуда пришли. Например, увеличение потенциала выполняется батарейками; когда электроны входят в ее отрицательную часть и выходят из положительной, напряжение батарейки возрастает. С другой стороны, когда электрон входит в резистор, требуется определенное усилие для того, чтобы провести его через этот резистор (вот почему резистор еще называют сопротивлением), отсюда и понижение потенциала при выходе из него электрона.
Используем правило контуров
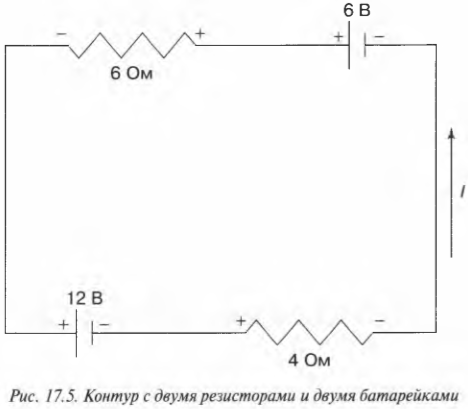
На рис. 17.5 показан пример использования правила контуров для цепи из двух резисторов и двух батареек. Ток какой силы идет по этой цепи?
Правило контуров гласит, что вдоль всего контура:
где \( \sum\!U \) — это сумма напряжений вдоль всего контура. Как можно использовать это правило?
Чтобы решить эту задачу, выберите направление тока, начертив стрелку, как показано на рис. 17.5. В действительности ток может идти в противоположном направлении, но здесь нет ничего плохого, ведь тогда полученная отрицательная сила тока будет показывать, что ток идет не в том направлении, которое было выбрано. Выбор направления тока — в данном примере против часовой стрелки — помогает начертить знаки + и — там, где ток соответственно заходит в резистор и выходит из него (эти действия в правило Кирхгофа не входят; я просто использую приемы, которые считаю полезными).
Известно, что вдоль всего контура \( \sum\!U \) = 0 и что в резисторе падение потенциала \( U = IR \). Остается только двигаться вдоль контура в одном направлении (не имеет значения, по часовой или против часовой стрелки), и когда встретится знак “+” или “-” (на резисторе или батарейке), нужно записать этот знак, а за ним — соответствующее ему падение или возрастание потенциала. Если, к примеру, начать с батарейки с э.д.с. 6 В и идти по часовой стрелке, то в соответствии с правилом контуров получим следующее равенство:
Сгруппировав его члены, получим:
и
Таким образом:
или
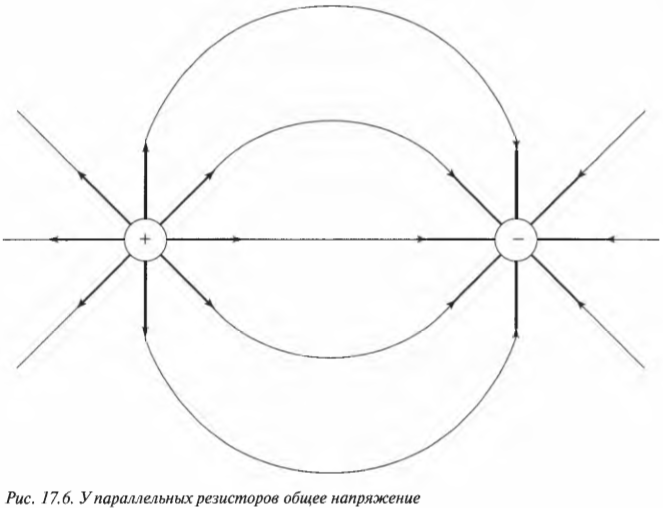
Итак, сила тока равна —0,6 А.
Из того, что сила тока имеет отрицательную величину, следует, что на самом деле ток идет в направлении, противоположном тому, которое выбрано сначала и показано на рис. 17.4.
Исследуем многоконтурные цепи
Если вам кажется, что правила Кирхгофа исчерпали все свои возможности уже на одноконтурных цепях, то попробуйте решить новую задачу, показанную на рис. 17.6.
На рисунке показаны три ответвления цепи и три разных тока. Найдите соответствующие значения сил тока \( I_1 \), \( I_2 \) и \( I_3 \) с применением обоих правил Кирхгофа. Правило соединения гласит, что в любом узле \( \sum\!I \) = 0, где \( \sum\!I \) — это сумма всех сил токов (втекающих и вытекающих). Рассмотрим точку А, которая находится в левой части рис. 17.6. Токи, соответствующие значениям \( I_1 \) и \( I_2 \), в нее втекают, а ток, соответствующий значению \( I_3 \), из нее вытекает, поэтому:
Теперь обратимся к правилу контуров, которое гласит, что \( \sum\!I \) = 0. В нашем примере три контура: два внутренних и один внешний, т.е. огибающий контур. Так как неизвестных у нас три (это значения силы тока \( I_1 \), \( I_2 \) и \( I_3 \)), то все, что нам нужно, — это три уравнения. Согласно правилу \( \sum\!I \) = 0, одно из них у нас уже есть. Поэтому, чтобы получить два оставшихся уравнения, надо разобраться с двумя внутренними контурами. Верхний контур дает:
А из нижнего контура получается:
Итак, получено три уравнения с тремя неизвестными:
Если значение \( I_3 \), полученное из первого уравнения, подставить во второе, тогда можно получить:
и
или
и
Используя первое из этих уравнений, можно \( I_1 \) выразить через \( I_2 \):
Подставив это значение \( I_1 \) во второе уравнение, получим:
или
Таким образом:
Теперь у нас есть одно из значений силы тока: \( I_2 \) = 6/11 А. Эту дробь можно вставить в уравнение:
чтобы получить:
После деления на 2 получим:
Тогда:
Теперь нам известны два значения сил токов \( I_2 \) и \( I_3 \). А как насчет \( I_1 \)? Так как:
то:
Отсюда легко получить, что:
Итак, благодаря правилам Кирхгофа, теперь нам известны все значения силы тока: \( I_1 \) = 15/11 А, \( I_2 \) = 6/11 А и \( I_3 \) = 21/11 А.
В подобных задачах доя поиска решения часто требуется потратить много времени и выполнить много вычислений, но, справившись с ними, можно полностью определить значения основных параметров электрических цепей.
Разбираемся с параллельно и последовательно соединенными конденсаторами
Параллельные и последовательные цепи можно создавать не только из резисторов, но и из конденсаторов. Как известно (подробнее см. главу 16), конденсатор — это физическая система, способная сохранять электрический заряд. Чтобы найти общую емкость конденсаторов, используемых в параллельной цепи, надо просто сложить их емкости:
Конденсаторы в параллельных цепях
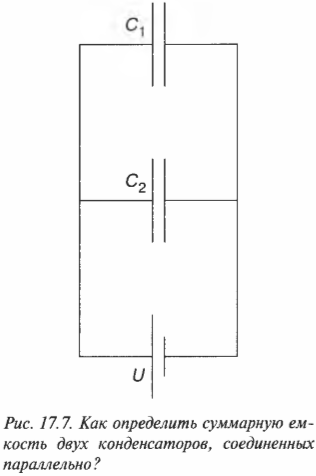
Когда конденсаторы подключены параллельно, то напряжение, создаваемое батарейкой, будет одинаковым для всех этих конденсаторов. Посмотрите на рис. 17.7, где показаны два конденсатора, подключенные в параллельную цепь.
Что же делать в подобной ситуации? Найдите общий заряд \( Q \), хранящийся на обоих конденсаторах \( C_1 \) и \( C_2 \); он равен сумме зарядов, хранящихся на каждом из них:
Так как батарейка подает на концы каждого конденсатора одно и то же напряжение \( U \), оно у конденсаторов одинаково, поэтому предыдущее равенство можно переписать как бы для одного конденсатора с емкостью \( C_1+C_2 \):
Иначе говоря, если заменить два конденсатора \( C_1 \) и \( C_2 \) одним \( C \), имеющим емкость \( C_1+C_2 \), то значение \( Q \) не изменится:
Конденсаторы в последовательных цепях
Когда конденсаторы включены параллельно, батарейка поддерживает одинаково напряжение на концах обоих конденсаторов.
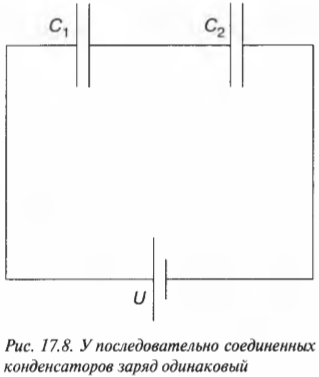
На рис. 17.8 показаны два конденсатора в последовательной цепи. Что же делать в такой ситуации?
Как видно на рис. 17.8, самая правая пластина конденсатора \( C_1 \) и самая левая пластина конденсатора \( C_2 \) соединены друг с другом, но не с остальной цепью. Иначе говоря, две пластины от остальной цепи изолированы, и вначале они электрически нейтральны (с суммарным общим зарядом, равным нулю).
Любой отрицательный заряд \( -q \), появившийся на самой правой пластине конденсатора \( C_1 \), должен быть равен по величине любому положительному заряду \( q \), появившемуся на самой левой пластине конденсатора \( C_2 \), поскольку суммарный заряд на обеих этих пластинах должен быть равен нулю. А так как суммарный заряд на двух пластинах одного конденсатора тоже должен быть равен нулю, то заряд на самой левой пластине конденсатора \( C_1 \) и на самой правой пластине конденсатора \( C_2 \) должен быть равен соответственно \( q \) и \( -q \). Поэтому величины зарядов (хоть отрицательных, хоть положительных) на каждой пластине одинаковы и равны \( q \).
Итак, заряд на каждом конденсаторе одинаковый. Кроме того, известно, что общее напряжение на концах двух конденсаторов вычисляется по формуле:
Так как заряд на каждом конденсаторе один и тот же, то это равенство принимает следующий вид:
Если вписать в равенство общую емкость \( C \), то получится:
Иначе говоря, последовательно подключенные емкости складываются так же, как и параллельно подключенные резисторы (см. выше раздел о параллельно подключенных резисторах): складываются обратные значения и берется значение .обратное результату:
Если конденсаторов больше двух, то сложение для них надо делать следующим образом:
Соединяем резисторы с конденсаторами: RC-цепи
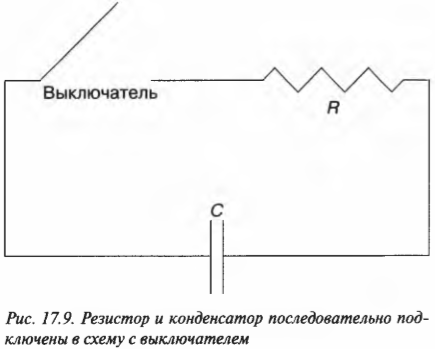
В предыдущих разделах этой главы речь шла о работающих отдельно друг от друга резисторах (электронных компонентах, затрудняющих движение тока в электрической цепи) и конденсаторах (телах, которые хранят заряд, держа его положительные и отрицательные компоненты отдельно, чтобы те притягивали друг друга, но при этом не могли самостоятельно соединиться). Теперь настало время собрать воедино резисторы и конденсаторы. Посмотрите на резистор и конденсатор, показанные на рис. 17.9. Допустим, что конденсатор в исходном состоянии имел напряжение \( U_0 \). Посмотрим, что произойдет после замыкания цепи с помощью выключателя. Может в цепи появится постоянный ток?
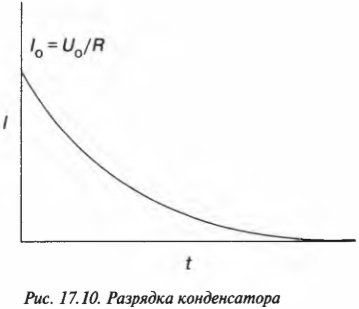
Но на самом деле ток ведет себя иначе: так, как показано на графике (рис. 17.10). Исходное значение силы тока равно (как и положено) \( U_0/R \) (где \( R \) означает сопротивление), но затем сила тока уменьшается. Что же происходит?
Дело в том, что с течением времени заряд конденсатора уменьшается и соответственно уменьшается ток. Конденсатор не является батарейкой и может подавать ток только тогда, когда на нем остается хоть какой-то заряд. Начальное значение силы тока равно \( U_0/R \), так как у конденсатора напряжение равно \( U_0 \), а ток идет через резистор \( R \). Но со временем ток слабеет по следующей формуле:
Здесь \( I \) — сила тока, \( e \) — основание натуральных логарифмов, равное 2,71828 (клавишу для вычисления значения функции \( e^{x} \) всегда можно найти на инженерном калькуляторе), \( t \) — время, \( R \) — сопротивление и \( C \) — это емкость. Подобно кривой, показанной на рис. 17.10, ведет себя и заряд конденсатора:






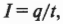
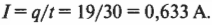
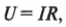
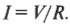
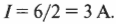
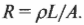
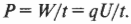
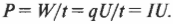
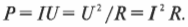
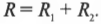
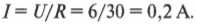
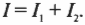
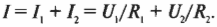
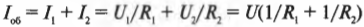
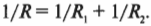
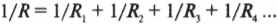
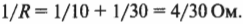
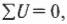
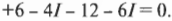
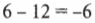
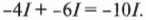
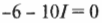
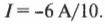
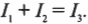
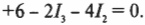
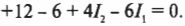
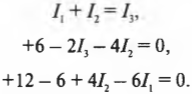
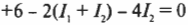
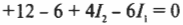
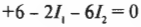
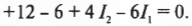
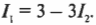
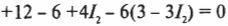
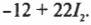
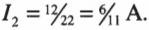
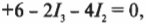
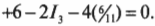
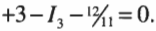
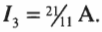
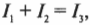
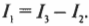
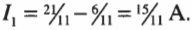
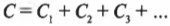
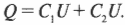
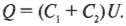
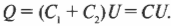
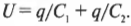
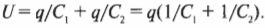
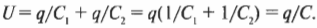
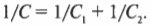
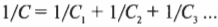
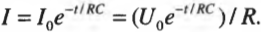
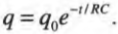
Добавить комментарий
[…] Источник […]
[…] Источник […]
[…] Источник […]
рис 17.6 опечатка
На рисунке 17.6 нет резисторов!
В ближайшее время исправим изображение
Так и не изменили…