Простые механизмы. КПД простых механизмов

1. Простые механизмы — приспособления, которые сконструировал и использовал человек, чтобы облегчить работу по перемещению тяжёлых предметов. К ним относят: рычаг, блок, наклонную плоскость. Разновидностями этих механизмов являются: клин, ворот и винт.

Все простые механизмы позволяют преобразовать силу, действующую на тело: либо уменьшить её, либо изменить её направление.

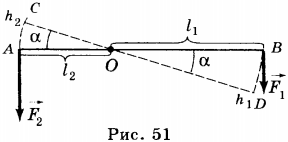
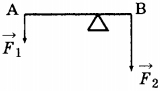
2. Рычаг — это стержень, вращающийся вокруг неподвижной опоры или оси (рис. 51). На рисунке показан рычаг, который может вращаться вокруг точки О, расположенный между концами рычага. К одному концу рычага подвешен груз, действующий на рычаг с силой \( F_1 \), равной весу груза. Действуя на длинный конец рычага с силой \( F_2 \), человек поднимает груз. При этом сила \( F_1 \) стремится повернуть рычаг по часовой стрелке, а груз \( F_2 \) — против часовой стрелки.

Плечом силы называют кратчайшее расстояние (перпендикуляр) от точки опоры до линии действия силы. Так, плечом силы \( F_1 \) является расстояние ОА \( (l_1) \), плечом силы \( F_2 \) — расстояние ОВ \( (l_2) \).

Из эксперимента следует, что рычаг находится в равновесии, если произведение силы, вращающей рычаг по часовой стрелке, и её плеча равно произведению силы, вращающей рычаг против часовой стрелки, и её плеча, т.е. \( F_1l_1=F_2l_2 \). Произведение силы, действующей на рычаг, и её плеча называют моментом силы: \( Fl=M \). Соответственно, если рычаг находится в равновесии, то \( M_1=M_2 \).

Условие равновесия рычага можно записать по-другому:\( \frac{F_1}{F_2}=\frac{l_2}{l_1} \). Это равенство означает, что рычаг находится в равновесии, если силы, действующие на него, обратно пропорциональны их плечам. Оно называется условием равновесия рычага.

Рычаг другого типа вращается вокруг точки, находящейся на конце рычага. Примером такого рычага может служить тачка. Когда используется такой рычаг, то вес груза направлен вниз, а человек действует на свободный конец рычага с силой, направленной вверх. Для такого рычага также справедливо условие равновесия, приведенное выше.

3. При подъеме груза работа силы, действующей на груз, равна \( A_1=F_1h_1 \), работа силы, приложенной к другому концу рычага, равна \( A_2=F_2h_2 \). Рассмотрение треугольников AOC и BOD позволяет сделать вывод о том, что они подобны и \( \frac{AO}{BO}=\frac{AC}{BD} \) или \( \frac{l_1}{l_2}=\frac{h_1}{h_2} \). Поскольку \( F_1l_1=F_2l_2 \), то \( F_1h_1=F_2h_2 \), т.е. \( A_1=2 \). Таким образом, рычаг, позволяя выиграть в силе, не даёт выигрыша в работе.

4. Ещё одним простым механизмом является блок. Блок — это колесо с желобом, по которому пропускается трос и которое может вращаться относительно оси О (см. рис. ниже).

Если ось блока закреплена, то блок не перемещается, и он называется неподвижным.

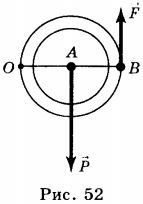
Неподвижный блок можно рассматривать как рычаг, вращающийся вокруг точки, лежащей посередине рычага. Плечи такого рычага равны друг другу: OA = OB. В соответствии с условием равновесия рычага приложенные к блоку силы тоже равны: \( P=F \). Следовательно, неподвижный блок не даёт выигрыша в силе, но он позволяет поднимать груз, прикладывая силу, направленную не вверх, а вниз, что облегчает перемещение груза.

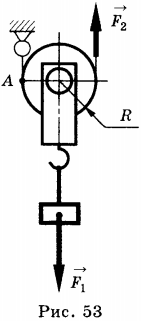
Чтобы получить выигрыш в силе используют подвижный блок (рис. 53). К нему непосредственно прикрепляется груз, один конец троса закрепляется, а к другому прикладывают силу и, таким образом, перебирая трос, поднимают блок с грузом.

В этом случае точкой вращения блока является точка А (см. рис. 52).

Плечи действующих сил равны соответственно: AO и AB, при этом AB = 2AO. В соответствии с условием равновесия рычага: \( P=2F \). Таким образом, подвижный блок даёт выигрыш в силе в 2 раза: \( F=P/2 \).

Измерив расстояние \( h_1 \), которое проходит груз, и расстояние \( h_2 \), на которое перемещается конец троса, можно обнаружить, что расстояние \( h_2=2h_1 \). Таким образом, подвижный блок даёт выигрыш в силе в 2 раза и в 2 раза проигрыш в пути. Соответственно, работа \( Ph_1=Fh_2 \), т.е. \( A_1=2 \). Подвижный блок, так же как и рычаг, не даёт выигрыша в работе.

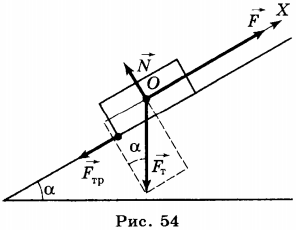
5. Наклонная плоскость используется в том случае, если нужно поднять объемный тяжёлый груз на какую-либо высоту (рис. 54).

Например, нужно погрузить ящик с металлическими деталями в кузов грузовика. В этом случае кладут массивную доску так, что она образует наклонную плоскость, один конец которой находится на земле, а другой на грузовике, и по этой плоскости втаскивают ящик. Чтобы поднять ящик вертикально вверх нужно приложить к нему силу, равную его весу \( P \). Перемещая равномерно ящик по наклонной плоскости, в отсутствие трения прикладывают силу, равную \( F=P\sin\alpha \), т.е. меньшую веса ящика, но при этом, выигрывая в силе, проигрывают в расстоянии. Работа по подъёму ящика по вертикали равна работе, совершаемой при его перемещении вдоль наклонной плоскости. Это справедливо, если сила сопротивления движению пренебрежимо мала. При наличии трения перемещение ящика вдоль наклонной плоскости требует совершения большей работы, чем при его движении вертикально вверх. В этом случае говорят о коэффициенте полезного действия (КПД) наклонной плоскости. Он равен отношению полезной работы ко всей совершённой работе: \( \mathbf{КПД}=A_п/A_с\cdot 100 \% \), где \( A_п \) — полезная работа, \( A_п=mgh \); \( A_с \) — совершённая работа при перемещении ящика вдоль наклонной плоскости, \( A_c=Fl \), где \( F \) — приложенная сила, \( l \) — длина наклонной плоскости.

Содержание

ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
Ответы

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Исследуя условия равновесия рычага, ученик выполнил соответствующую лабораторную работу. В таблице представлены значения сил и их плеч для рычага, находящегося в равновесии. Определите, чему равно плечо \( l_1 \)?

1) 12,8 м
2) 2,5 м
3) 0,8 м
4) 0,25 м

2. Ученик выполнял лабораторную работу по исследованию условий равновесия рычага. Результаты для сил и их плеч, которые он получил, представлены в таблице.

Чему равна сила \( F_1 \), если рычаг находится в равновесии?

1) 100 Н
2) 50 Н
3) 25 Н
4) 9 Н

3. Рычаг находится в равновесии под действием двух сил. Сила \( F_1 \) = 6 Н. Чему равна сила \( F_2 \), если длина рычага 50 см, а плечо силы \( F_1 \) равно 30 см?

1) 0,1 Н
2) 3,6 Н
3) 9 Н
4) 12 Н

4. Выигрыш в силе, приложенной к грузу, нельзя получить с помощью

1) подвижного блока
2) неподвижного блока
3) рычага
4) наклонной плоскости

5. С помощью неподвижного блока в отсутствие трения силе

1) выигрывают в 2 раза
2) не выигрывают, но и не проигрывают
3) проигрывают в 2 раза
4) возможен и выигрыш, и проигрыш

6. С помощью подвижного блока в отсутствие трения

1) выигрывают в работе в 2 раза
2) проигрывают в силе в 2 раза
3) не выигрывают в силе
4) выигрывают в силе в 2 раза

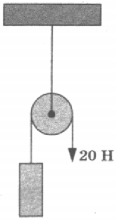
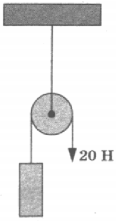
7. На рисунке изображён неподвижный блок, с помощью которого, прикладывая к свободному концу нити силу 20 Н, равномерно поднимают груз. Если трением пренебречь, то масса поднимаемого груза равна

1) 4 кг
2) 2 кг
3) 0,5 кг
4) 1 кг

8. Наклонная плоскость даёт выигрыш в силе в 2 раза. В работе при отсутствии силы трения эта плоскость

1) даёт выигрыш в 2 раза
2) даёт выигрыш в 4 раза
3) не даёт ни выигрыша, ни проигрыша
4) даёт проигрыш в 2 раза

9. Вдоль наклонной плоскости длиной 5 м поднимают груз массой 40 кг, прикладывая силу 160 Н. Чему равна высота наклонной плоскости, если трение при движении груза пренебрежимо мало?

1) 1,25 м
2) 2 м
3) 12,5 м
4) 20 м

10. Груз массой 10 кг поднимают по наклонной плоскости длиной 2 м и высотой 0,5 м, прикладывая силу 40 Н. Чему равен КПД наклонной плоскости?

1) 160%
2) 62,5%
3) 16%
4) 6,25%

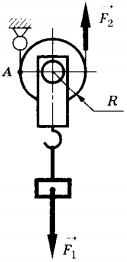
11. Груз поднимают с помощью подвижного блока радиусом \( R \) (см. рисунок). Установите соответствие между физическими величинами (левый столбец) и формулами, по которым они определяются (правый столбец).

Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) плечо силы \( \vec{F}_1 \) относительно точки A
Б) плечо силы \( \vec{F}_2 \) относительно точки A
B) момент силы \( \vec{F}_1 \) относительно точки A

ФОРМУЛЫ
1) \( F_1R \)
2) \( 2F_1R \)
3) \( \frac{F_1}{R} \)
4) \( R \)
5) \( 2R \)

12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.

1) Любой простой механизм даёт выигрыш в силе.
2) Ни один простой механизм не даёт выигрыша в работе.
3) Наклонная плоскость выигрыша в силе не даёт.
4) Коэффициент полезного действия показывает, какая часть совершенной работы является полезной.
5) Неподвижный блок даёт выигрыш в силе в 2 раза.

Часть 2

13. Чему равна сила, с которой действуют на брусок массой 0,2 кг, перемещая его по наклонной плоскости длиной 1,6 м и высотой 0,4 м, если КПД наклонной плоскости 80%.