Потенциальная и кинетическая энергия. Закон сохранения механической энергии

1. Камень, упав с некоторой высоты на Землю, оставляет на поверхности Земли вмятину. Во время падения он совершает работу по преодолению сопротивления воздуха, а после касания земли — работу по преодолению силы сопротивления почвы, поскольку обладает энергией. Если накачивать в закрытую пробкой банку воздух, то при некотором давлении воздуха пробка вылетит из банки, при этом воздух совершит работу по преодолению трения пробки о горло банки, благодаря тому, что воздух обладает энергией. Таким образом, тело может совершить работу, если оно обладает энергией. Энергию обозначают буквой \( E \). Единица работы — \( [E\,] \) = 1 Дж.
При совершении работы изменяется состояние тела и изменяется его энергия. Изменение энергии равно совершенной работе: \( E=A \).
2. Потенциальной энергией называют энергию взаимодействия тел или частей тела, зависящую от их взаимного положения.
Поскольку тела взаимодействуют с Землёй, то они обладают потенциальной энергия взаимодействия с Землёй.
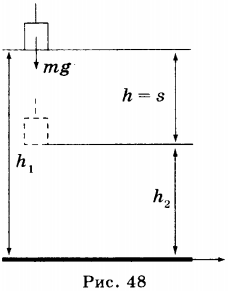
Если тело массой \( m \) падает с высоты \( h_1 \) до высоты \( h_2 \), то работа силы тяжести \( F_т \) на участке \( h=h_1-h_2 \) равна: \( A = F_тh = mgh = mg(h_1 — h_2) \) или \( A = mgh_1 — mgh_2 \) (рис. 48).
В полученной формуле \( mgh_1 \) характеризует начальное положение (состояние) тела, \( mgh_2 \) характеризует конечное положение (состояние) тела. Величина \( mgh_1=E_{п1} \) — потенциальная энергия тела в начальном состоянии; величина \( mgh_2=E_{п2} \) — потенциальная энергия тела в конечном состоянии.
Можно записать \( A=E_{п1}-E_{п2} \), или \( A=-(E_{п2}-E_{п1}) \), или \( A=-E_{п} \).
Таким образом, работа силы тяжести равна изменению потенциальной энергии тела. Знак «–» означает, что при движении тела вниз и соответственно при совершении силой тяжести положительной работы потенциальная энергия тела уменьшается. Если тело поднимается вверх, то работа силы тяжести отрицательна, а потенциальная энергия тела увеличивается.
Если тело находится на некоторой высоте \( h \) относительно поверхности Земли, то его потенциальная энергия в данном состоянии равна \( E_п=mgh \). Значение потенциальной энергии зависит от того, относительно какого уровня она отсчитывается. Уровень, на котором потенциальная энергия равна нулю, называют нулевым уровнем.
В отличие от кинетической энергии потенциальной энергией обладают покоящиеся тела. Поскольку потенциальная энергия — это энергия взаимодействия, то она относится не к одному телу, а к системе взаимодействующих тел. В данном случае эту систему составляют Земля и поднятое над ней тело.
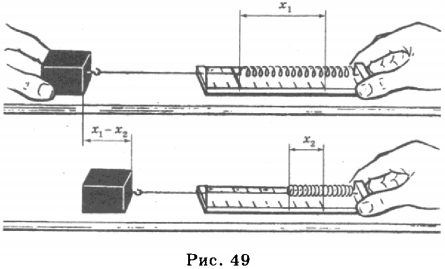
3. Потенциальной энергией обладают упруго деформированные тела. Предположим, что левый конец пружины закреплён, а к правому её концу прикреплён груз. Если пружину сжать, сместив правый её конец на \( x_1 \), то в пружине возникнет сила упругости \( F_{упр1} \), направленная вправо (рис. 49).
Если теперь предоставить пружину самой себе, то её правый конец переместится, удлинение пружины будет равно \( x_2 \), а сила упругости \( F_{упр2} \).
Работа силы упругости равна
\[ A=F_{ср}(x_1-x_2)=k/2(x_1+x_2)(x_1-x_2)=kx_1^2/2-kx_2^2/2 \]
\( kx_1^2/2=E_{п1} \) — потенциальная энергия пружины в начальном состоянии, \( kx_2^2/2=E_{п2} \) — потенциальная энергия пружины во конечном состоянии. Работа силы упругости равна изменению потенциальной энергии пружины.
Можно записать \( A=E_{п1}-E_{п2} \), или \( A=-(E_{п2}-E_{п1}) \), или \( A=-E_{п} \).
Знак «–» показывает, что при растяжении и сжатии пружины сила упругости совершает отрицательную работу, потенциальная энергия пружины увеличивается, а при движении пружины к положению равновесия сила упругости совершает положительную работа, а потенциальная энергия уменьшается.
Если пружина деформирована и её витки смещены относительно положения равновесия на расстояние \( x \), то потенциальная энергия пружины в данном состоянии равна \( E_п=kx^2/2 \).
4. Движущиеся тела так же могут совершить работу. Например, движущийся поршень сжимает находящийся в цилиндре газ, движущийся снаряд пробивает мишень и т.п. Следовательно, движущиеся тела обладают энергией. Энергия, которой обладает движущееся тело, называется кинетической энергией. Кинетическая энергия \( E_к \) зависит от массы тела и его скорости \( E_к=mv^2/2 \). Это следует из преобразования формулы работы.
Работа \( A=FS \). Сила \( F=ma \). Подставив это выражение в формулу работы, получим \( A=maS \). Так как \( 2aS=v^2_2-v^2_1 \), то \( A=m(v^2_2-v^2_1)/2 \) или \( A=mv^2_2/2-mv^2_1/2 \), где \( mv^2_1/2=E_{к1} \) — кинетическая энергия тела в первом состоянии, \( mv^2_2/2=E_{к2} \) — кинетическая энергия тела во втором состоянии. Таким образом, работа силы равна изменению кинетической энергии тела: \( A=E_{к2}-E_{к1} \), или \( A=E_к \). Это утверждение — теорема о кинетической энергии.
Если сила совершает положительную работу, то кинетическая энергия тела увеличивается, если работа силы отрицательная, то кинетическая энергия тела уменьшается.
5. Полная механическая энергия \( E \) тела — физическая величина, равная сумме его потенциальной \( E_п \) и кинетической \( E_п \) энергии: \( E=E_п+E_к \).
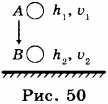
Пусть тело падает вертикально вниз и в точке А находится на высоте \( h_1 \) относительно поверхности Земли и имеет скорость \( v_1 \) (рис. 50). В точке В высота тела \( h_2 \) и скорость \( v_2 \) Соответственно в точке А тело обладает потенциальной энергией \( E_{п1} \) и кинетической энергией \( E_{к1} \), а в точке В — потенциальной энергией \( E_{п2} \) и кинетической энергией \( E_{к2} \).
При перемещении тела из точки А в точку В сила тяжести совершает работу, равную А. Как было показано, \( A=-(E_{п2}-E_{п1}) \), а также \( A=E_{к2}-E_{к1} \). Приравняв правые части этих равенств, получаем: \( -(E_{п2}-E_{п1})=E_{к2}-E_{к1} \), откуда \( E_{к1}+E_{п1}=E_{п2}+E_{к2} \) или \( E_1=E_2 \).
Это равенство выражает закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которыми действуют консервативные силы (силы тяготения или упругости) сохраняется.
В реальных системах действуют силы трения, которые не являются консервативными, поэтому в таких системах полная механическая энергия не сохраняется, она превращается во внутреннюю энергию.
Содержание
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Два тела находятся на одной и той же высоте над поверхностью Земли. Масса одного тела \( m_1 \) в три раза больше массы другого тела \( m_2 \). Относительно поверхности Земли потенциальная энергия
1) первого тела в 3 раза больше потенциальной энергии второго тела
2) второго тела в 3 раза больше потенциальной энергии первого тела
3) первого тела в 9 раз больше потенциальной энергии второго тела
4) второго тела в 9 раз больше потенциальной энергии первого тела
2. Сравните потенциальную энергию мяча на полюсе \( E_п \) Земли и на широте Москвы \( E_м \), если он находится на одинаковой высоте относительно поверхности Земли.
1) \( E_п=E_м \)
2) \( E_п>E_м \)
3) \( E_п<E_м \)
4) \( E_п\geq E_м \)
3. Тело брошено вертикально вверх. Его потенциальная энергия
1) одинакова в любые моменты движения тела
2) максимальна в момент начала движения
3) максимальна в верхней точке траектории
4) минимальна в верхней точке траектории
4. Как изменится потенциальная энергия пружины, если её удлинение уменьшить в 4 раза?
1) увеличится в 4 раза
2) увеличится в 16 раз
3) уменьшится в 4 раза
4) уменьшится в 16 раз
5. Лежащее на столе высотой 1 м яблоко массой 150 г подняли относительно стола на 10 см. Чему стала равной потенциальная энергия яблока относительно пола?
1) 0,15 Дж
2) 0,165 Дж
3) 1,5 Дж
4) 1,65 Дж
6. Скорость движущегося тела уменьшилась в 4 раза. При этом его кинетическая энергия
1) увеличилась в 16 раз
2) уменьшилась в 16 раз
3) увеличилась в 4 раза
4) уменьшилась в 4 раза
7. Два тела движутся с одинаковыми скоростями. Масса второго тела в 3 раза больше массы первого. При этом кинетическая энергия второго тела
1) больше в 9 раз
2) меньше в 9 раз
3) больше в 3 раза
4) меньше в 3 раза
8. Тело падает на пол с поверхности демонстрационного стола учителя. (Сопротивление воздуха не учитывать.) Кинетическая энергия тела
1) минимальна в момент достижения поверхности пола
2) минимальна в момент начала движения
3) одинакова в любые моменты движения тела
4) максимальна в момент начала движения
9. Книга, упавшая со стола на пол, обладала в момент касания пола кинетической энергией 2,4 Дж. Высота стола 1,2 м. Чему равна масса книги? Сопротивлением воздуха пренебречь.
1) 0,2 кг
2) 0,288 кг
3) 2,0 кг
4) 2,28 кг
10. С какой скоростью следует бросить тело массой 200 г с поверхности Земли вертикально вверх, чтобы его потенциальная энергия в наивысшей точке движения была равна 0,9 Дж? Сопротивлением воздуха пренебречь. Потенциальную энергию тела отсчитывать от поверхности земли.
1) 0,9 м/с
2) 3,0 м/с
3) 4,5 м/с
4) 9,0 м/с
11. Установите соответствие между физической величиной (левый столбец) и формулой, по которой она вычисляется (правый столбец). В ответе запишите подряд номера выбранных ответов
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия взаимодействия тела с Землёй
Б. Кинетическая энергия
B. Потенциальная энергия упругой деформации
ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) \( E=mv^2/2 \)
2) \( E=kx^2/2 \)
3) \( E=mgh \)
12. Мяч бросили вертикально вверх. Установите соответствие между энергией мяча (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия
Б. Кинетическая энергия
B. Полная механическая энергия
ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) Уменьшается
2) Увеличивается
3) Не изменяется
Часть 2
13. Пуля массой 10 г, движущаяся со скоростью 700 м/с, пробила доску толщиной 2,5 см и при выходе из доски имела скорость 300 м/с. Определить среднюю силу сопротивления, воздействующую на пулю в доске.







Добавить комментарий
привет
Салам