Глава 14. Передаем тепловую энергию в твердых телах и газах

В этой главе …
- Передаем тепловую энергию с помощью теплопроводности, конвекции и излучения
- Изучаем газы и число Авогадро
- Исследуем идеальный газ
- Знакомимся с молекулами идеального газа
Передачу теплоты и вызванные этой передачей химические изменения можно наблюдать практически ежедневно в окружающих нас бытовых ситуациях. Например, при варке макарон конвективные потоки воды в кастрюле закручивают в вихри отдельные макаронины. Если схватить кастрюлю с кипящей водой за ее металлические ручки, то можно обжечь руки из-за интенсивной теплопроводности металла. В яркий солнечный летний день можно сразу почувствовать, как лицо нагревается от излучения тепла солнцем.
Однако учтите, что если во время свидания вы вдруг ощущаете необыкновенное тепло, то скорее всего оно от волнения и взаимности симпатий, а не от физической передачи тепловой энергии.
В начале этой главы рассматриваются три основные способа распространения тепловой энергии. Затем речь идет о том, как тепловая энергия воздействует на газы: здесь можно найти базовые сведения о молях и определении числа молекул в некоторых жидкостях или твердых телах. Далее рассказывается, как тепловая энергия распространяется вокруг нас, какое количество молекул принимает участие в таких взаимодействиях в некоторых ситуациях и т.д. Прочитав эту главу, вы сможете поразить своих приятелей на вечеринках, легко и непринужденно сообщая им о том, какое чудовищно большое количество молекул воды содержится в их стаканах!
Содержание
Кипятим воду: конвекция
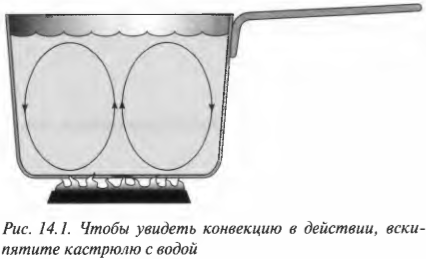
Конвекция — один из основных способов передачи тепловой энергии из одного места в другое. Она происходит при нагревании вещества, подобного, например, воздуху или воде. Дело в том, что при нагреве некоторая более теплая часть вещества становится менее плотной, чем остальная более холодная часть, и эта теплая и менее плотная часть поднимается вверх. Посмотрите (рис. 14.1) на кастрюлю, в которой нагревается вода. Как тепловая энергия переносится в воде? Вода поблизости от нагревательного элемента нагревается, расширяется и становится менее плотной. Нагретая менее плотная вода поднимается вверх, а охладившаяся и, следовательно, более плотная, опускается вниз, в результате чего возникают восходящие и нисходящие потоки воды. Чтобы увидеть, как происходит конвекция, бросьте в кастрюлю немного мелкой лапши и понаблюдайте за ее циркуляцией (повторяющимися движениями вверх и вниз). Здесь передатчиком тепловой энергии является движущаяся вода.
Впрочем, конвекция может обойтись и без воды; то же явление происходит с воздухом и многими другими веществами. Возможно, вы видели, как птицы, летая кругами и поднимаясь все выше и выше, парят в восходящих потоках теплого воздуха. Эти потоки создаются конвективным движением воздуха, нагретого у поверхности земли.
Многие печи работают на основе конвекции. Возможно, вы слышали термин “конвективная печь”, используемый, скажем так, в противоположность термину “микроволновая печь”. Воздух внутри конвективной печи нагревается, в результате чего происходит циркуляция потоков воздуха. А микроволновая печь с помощью сверхвысокочастотной электромагнитной волны поляризует молекулы в пище и заставляет их вибрировать. Поэтому, хотите — верьте, хотите — нет, нагревание в микроволновке на самом деле происходит из-за трения.
Возможно, вы слышали выражение “поднимается жара”. Оно-то и относится к конвекции. Горячий воздух расширяется и становится менее плотным, чем находящийся вокруг него холодный воздух. В результате этого горячий воздух поднимается. Таким образом, если у вас имеется двух- или трехэтажный дом с открытым лестничным маршем, тогда весь воздух, заботливо нагреваемый вами зимой, будет благополучно собираться на самом верхнем этаже. Кроме того, конвекция поднимает в комнатах тепловую энергию от радиаторов отопления, приводя в некоторой степени к циркуляции окружающего воздуха. Чтобы усилить распространение тепловой энергии, кое-кто использует потолочные вентиляторы. Если ранее вы сталкивались с такими проявлениями конвекции, то теперь знаете принцип ее работы. Впрочем, имеются и другие явления, связанные с нагреванием, о которых вы и не подозреваете. Так что читайте дальше!
Слишком жарко, чтобы держать в руках: теплопроводность
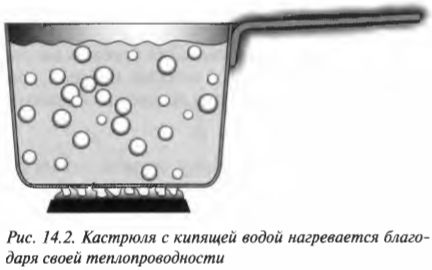
С помощью теплопроводности тепловая энергия передается прямо через материал, без помощи каких-либо потоков, как при конвекции (см. предыдущий раздел). Посмотрите на металлическую кастрюлю (рис. 14.2) и на ее металлическую ручку. Содержимое кастрюли кипит уже в течение 15 минут. Стоит ли брать ее с огня, хватаясь за ручку без кухонной рукавицы? Скорее всего, нет, если только вы не ищете острых ощущений. Конечно, металлическая ручка горячая, но почему? Да уж точно не из-за конвекции, так как здесь нет конвективных потоков вещества. Ручка горячая из-за наличия теплопроводности.
А теперь перейдем на молекулярный уровень. Молекулы, расположенные поблизости от источника тепловой энергии, нагреваются и начинают двигаться быстрее. Они сталкиваются с соседними молекулами и таким образом заставляют их двигаться быстрее (что подтвердит любой, кто играет в бильярд). Эти учащающиеся столкновения и нагревают вещество.
Одни материалы, например, большинство металлов, проводят тепловую энергию лучше других, например, таких, как фарфор, дерево или стекло. То, каким образом материалы проводят тепло, в значительной мере зависит от их молекулярной структуры, так что разные материалы проводят тепло по-разному.
Холодное и теплое ощущения от соприкосновения
Почему металлы на ощупь такие холодные? Любой металлический предмет на ощупь кажется более холодным (даже если он не находится в холодильнике, как, например, банка с пивом), чем деревянный. Этот факт повседневной жизни не вызывает удивления. Но в чем его причина? Все объясняется теплопроводностью. Металлы обладают гораздо большей теплопроводностью, чем, например, деревянная поверхность стола, и потому гораздо быстрее отводят тепловую энергию от пальцев.
Выводим формулу теплопроводности
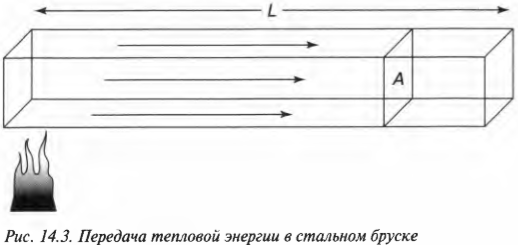
Чтобы изучать передачу тепловой энергии в физических телах, выполняемую с помощью теплопроводности, необходимо учитывать различные их свойства. Например, для стального бруска надо учитывать его площадь и длину, а также температуру в разных его частях. Посмотрите на рис. 14.3, где показан стальной брусок, нагреваемый с одного конца и передающий оттуда тепловую энергию по направлению к другому концу. Можно сказать, с какой скоростью проходит эта передача? Да никаких проблем.
В этой ситуации можно пойти двумя разными путями. Например, нетрудно предположить, что, чем больше разница температур между концами бруска, тем интенсивнее передается тепловая энергия. Оказывается, что количество переданной тепловой энергии \( Q \) пропорционально разнице температур \( \Delta{T} \) (символ \( \propto \) означает “пропорционально”):
С другой стороны, разумно было бы ожидать, что брусок в два раза большей ширины способен передать в два раза больше тепловой энергии. В общем, количество переданной тепловой энергии \( Q \) пропорционально площади поперечного сечения \( A \):
А чем брусок длиннее, тем меньше тепловой энергии дойдет до другого его конца; и действительно, переданная тепловая энергия оказывается обратно пропорциональной длине бруска, равной \( L \):
И наконец, количество переданной тепловой энергии \( Q \) зависит от величины прошедшего времени \( t \). Вот как это выражается математически:
Собрав это все воедино и обозначив буквой \( k \) константу (т.е. некую постоянную величину), которую еще предстоит определить, вы получите следующую формулу передачи тепловой энергии через тот или иной материал:
Таким способом определяется количество тепловой энергии, передаваемое с помощью теплопроводности за данный промежуток времени \( t \) через определенную длину \( L \), когда площадь поперечного сечения равна \( A \). Используемая в формуле постоянная \( k \) — это и есть теплопроводность материала, которая измеряется в Дж/с·м·°С.
Разные материалы (стекло, сталь, медь, жевательная резинка) проводят тепловую энергию с разной скоростью, поэтому постоянная теплопроводности зависит от используемого материала. К счастью, физики уже измерили значения этой постоянной для различных материалов. Некоторые из результатов этих измерений показаны в табл. 14.1.
Применяем формулу теплопроводности
Теплопроводность стальной части ручки кастрюли равна 14,0 Дж/с·м·°С (см. табл. 14.1). Посмотрите на рис. 14.3. Если длина ручки равна 15 см, площадь ее поперечного сечения составляет 2,0 см2, а температура огня с одного конца ручки равна 600°С, то сколько тепловой энергии вы получите после того, как возьметесь за эту ручку? Вот формула передачи тепловой энергии с помощью теплопроводности:
При условии, что у холодного конца ручки начальная температура равна комнатной, т.е. 25°С, вам достанется:
Как стать инженером холодильной установки
Веря за основу свойства теплопроводности или теплоизоляции различных материалов, можно выяснить, как сохранять предметы холодными или горячими, начиная с напитков и кончая хот-догами и стеллажами с мясом. Представьте себе, например, что нужно спроектировать специальное морозильное отделение в хранилище для замороженных продуктов. Первое, что приходит в голову: а не сделать ли это специальное отделение из меди, чья теплопроводность равна 390 Дж/с·м·°С. Впрочем, такой выбор материала может привести к печальным последствиям, так как из-за очень высокой теплопроводности меди тепло будет легко поступать в это специальное морозильное отделение и легко из него выходить. Лучше обратиться к теплопроводности других материалов. Теплопроводность пенопласта равна только 0,01 Дж/с·м·°С, что во много раз лучше. Если в медном морозильном отделении лед может храниться в течение времени, равного \( t \), то в морозильном отделении, построенном с использованием пенопласта, лед может храниться в 390/0,01 = 39000 раз дольше. (Конечно, это всего лишь прикидка; на самом деле ответ зависит и от теплопроводности того, что будет храниться в морозильном отделении.)
Как видите, каждую секунду к концу ручки передается 10,7 Дж тепловой энергии. И так с каждой секундой количество переданных джоулей будет все больше и больше, делая ручку все горячее и горячее.
Испускаем и поглощаем свет: тепловое излучение
Как быстро отогреться после прихода домой поздней осенью в мокрую и дождливую погоду? В определенной степени без участия физики здесь не обойтись. Конечно же, сразу же хочется принять теплую ванну! Обогреться можно не только теплой водой, но даже с помощью висящей в ванной лампы накаливания (рис. 14.4). Действительно, лампа накаливания испускает тепловую энергию и не дает вам мерзнуть.
Тепловое излучение — это свет, который может передавать тепловую энергию. Тепловую энергию, передаваемую с помощью излучения, мы получаем ежедневно в виде дневного света. Действительно, Солнце — это громадный тепловой реактор, расположенный от нас на расстоянии в 150 млн. км, и тепловая энергия, идущая от него через космический вакуум, попадает на Землю, не пользуясь теплопроводностью или конвекцией (см. два предыдущих раздела этой главы). На Земле солнечная энергия оказывается благодаря излучению, в чем можно убедиться самостоятельно, просто постояв в ясный день на улице и подставив лицо солнечным лучам. Впрочем, имеется еще один способ получить ощутимые признаки излучения, а именно заполучить солнечный ожог, с которым потом придется иметь дело.
Тепловое излучение: не видим, но ощущаем
Любое физическое тело вокруг вас является источником постоянного теплового излучения, если только оно не имеет температуру абсолютного нуля, что маловероятно, так как физически очень трудно достичь этой температуры. Например, порция мороженого тоже испускает тепловое излучение. Дело в том, что тепловое излучение — это не что иное, как электромагнитное излучение. Электромагнитное излучение возникает благодаря ускорению и замедлению электрических зарядов. На молекулярном уровне именно это и происходит при нагревании физических тел: атомы движутся с ускорением и довольно сильно взаимодействуют друг с другом.
Даже наши тела постоянно излучают энергию, только это электромагнитное излучение обычно не видно, так как находится в инфракрасной части спектра. Впрочем, этот свет виден в инфракрасные приборы, которые часто упоминаются как “приборы ночного видения”. Мы излучаем тепловую энергию постоянно по всем направлениям, а все предметы вокруг нас также постоянно излучают тепловую энергию по всем направлениям. Если у вас и окружающей вас среды одинаковая температура, то и вы, и эта среда излучаете энергию по направлению к друг другу с одинаковой интенсивностью.
Когда окружающая среда излучает недостаточно много тепловой энергии по направлению к вам, то возникает ощущение холода. Вот почему космос считается таким “холодным”. А ведь в нем нет ничего холодного на ощупь, и тепловая энергия в космосе не теряется из-за теплопроводности или конвекции. Единственное, что происходит, — это космическая среда слабо излучает по направлению к вам, а вы, благодаря собственному излучению, будете постоянно терять тепловую энергию и очень быстро начнете мерзнуть.
Когда тело нагрето примерно до 1000 К, оно начинает сиять красным светом (возможно, это и объясняет, почему вы, даже излучая, не сияете красным светом из видимой части спектра). А когда тело становится горячее, его излучение смещается через оранжевую, желтую и другие части спектра по направлению к его белой части, которая достигается где-то при 1700 К.
Нагреватели с накаляемой докрасна спиралью передают тепловую энергию с помощью теплового излучения. Что касается конвекции, то она происходит тогда, когда воздух нагревается, поднимается вверх и распространяется по комнате (а передача тепловой энергии с помощью теплопроводности — тогда, когда вы по ошибке прикоснетесь к горячей части нагревателя, что вряд ли можно назвать удачным примером теплопередачи). Впрочем, от нагревателя со спиралью накаливания передача тепловой энергии происходит в основном через излучение. В настоящее время во многих домах имеются нагревательные провода, вмонтированные в стены, потолки или полы и называемые нагревателями лучистого отопления. Этих нагревателей по замыслу архитектора не видно, но если стать лицом к одному из них, сразу почувствуется тепло, вызванное тепловым излучением.
Люди интуитивно понимают, что такое излучение и поглощение тепловой энергии в окружающей среде. Например, всем известно, что в жаркий день лучше не одевать черную тенниску, так как в ней будет жарко. Почему? По сравнению с белой тенниской она поглощает больше, а отражает меньше света, полученного из окружающей среды. Следовательно, в белой тенниске будет прохладнее и именно потому, что она отражает в окружающую среду больше теплового излучения. В какую машину вы предпочтете сесть в жаркий день: в обитую черной или белой кожей?
Излучение и “черные тела”
Некоторые тела поглощают падающий на них свет в большей степени, чем все остальные. Тела, которые поглощают все падающее на них тепловое излучение, имеют отдельное название — “черные тела”. “Черное тело” поглощает 100% падающего на него теплового излучения, и если оно находится в равновесии с окружающей его средой, то столько же теплового излучения оно испускает в эту среду.
Большинство физических тел находится между зеркалами и “черными телами”, которые, соответственно, отражают или поглощают весь падающий на них свет. Обычные тела “с серединки на половинку”, относящиеся к этому большинству, поглощают часть падающего на них света и затем снова испускают его в окружающую среду. Блестящие тела являются такими потому, что отражают большинство падающего на них света. Темные тела выглядят такими потому, что отражают мало падающего на них света.
Можно немало узнать о физике “черных тел”, если начать с вопроса: сколько тепловой энергии испускает “черное тело” при заданной температуре? Количество испускаемой тепловой энергии пропорционально времени испускания: например, за в два раза больший промежуток времени тепловой энергии испускается в два раза больше. Так что можно написать следующую формулу, где \( t \) — это время:
Нетрудно сообразить, что количество теплового излучения пропорционально общей площади, с которой происходит излучение. Поэтому можно написать еще одну формулу, где \( A \) — это площадь, с которой происходит излучение:
Где-то в формуле должна быть температура \( T \): чем тело теплее, тем больше оно излучает тепловой энергии. В ходе экспериментов выяснилось, что количество излучаемой тепловой энергии пропорционально температуре в четвертой степени, \( T^4 \). Таким образом, получается, что:
Чтобы придать формуле законченный вид, в нее надо вставить постоянную, которую находят экспериментально. Тепловую энергию, испускаемую “черным телом”, вычисляют, используя входящую в ее формулу постоянную Стефана-Больцмана \( \sigma \).
Значение \( \sigma \) равно 5,67·10-8 Дж(с·м2·К4). Впрочем, обратите внимание, что эта постоянная подходит только для “черных тел”, которые являются идеальными излучателями. Но большинство тел идеальными излучателями не является, поэтому в большинстве случаев приходится вставлять еще и другую постоянную — ту, которая зависит от используемого вещества. Эта постоянная называется излучательной (эмиссионной) способностью — \( e \). Таким образом, искомая формула, или закон излучения Стефана-Больцмана, принимает такой вид:
где \( e \) — излучательная (эмиссионная) способность тела, \( \sigma \) — постоянная Стефана-Больцмана (5,67·10-8 Дж(с·м2·К4)), \( A \) — излучающая площадь, \( t \) — время, а \( T \) — температура в кельвинах.
Допустим, что у некоего человека излучательная способность примерно равна 0,8. Сколько тепловой энергии излучает он каждую секунду при условии, что температура его тела равна 37°С? Во-первых, надо вычислить, чему равна площадь, с которой происходит тепловое излучение. Математически приняв этого человека за цилиндр высотой 1,6 м и радиусом 0,1 м, вы получите общую площадь поверхности как:
где \( r \) и \( h \) — это, соответственно, радиус и высота. Чтобы найти общую тепловую энергию, излучаемую этим человеком, вставьте числа в формулу закона излучения Стефана-Больцмана:
Итак, получается 449 Дж/сек, или 449 Вт. Это значение может показаться высоким, так как температура кожи не так высока, как температура внутренней части тела, но здесь мы имеем дело с приблизительными величинами.
Разбираемся с числом Авогадро
В этой главе в основном говорится о действии тепловой энергии на твердые тела и жидкости (например, в сосудах с жидким металлом), но много нового здесь можно узнать о процессах нагрева газов. Сначала разберемся, с каким количеством молекул приходится иметь дело. Для этого нам потребуется не слишком много знаний по физике. Представьте, что некто нашел большой алмаз и принес его вам для оценки.
“Сколько атомов в моем алмазе?”
“Это зависит от того, сколько в нем молей,” — отвечаете вы.
Человек, обидевшись, говорит: “Попрошу не выражаться!”
Моль — это количество атомов в 12 г углерода изотопа 12. Углерод изотопа 12 (обозначается как 12С, а также называется углеродом-12, или просто углеродом 12) — это наиболее распространенный вариант углерода, хотя в некоторых атомах углерода имеется чуть больше нейтронов (в углероде-13 уж точно), поэтому их в среднем получается где-то 12,011. Перед тем как узнать, сколько у вас атомов, выясните, сколько молей вещества находится в вашем распоряжении, а при работе с газами часто требуется знать количество атомов.
В результате измерений было найдено, что количество атомов в моле (так называемое число Авогадро, \( N_А \)) равно 6,022·1023. Итак, теперь вы знаете, сколько атомов находится в 12 г углерода-12. Будет ли то же количество атомов, скажем, в 12 г серы? Ни в коем случае. Каждый атом серы по весу отличается от каждого атома углерода, так что даже в одинаковом количестве граммов каждого из этих веществ будет разное количество атомов.
Насколько масса серы больше массы углерода-12? Изучив таблицу Менделеева, висящую на стене физической лаборатории, вы узнаете, что атомная масса серы равна 32,06 (обычно это число, расположенное правее и ниже символа элемента, например, для серы таким символом является S). Но чего именно 32,06? Имеются в виду 32,06 атомных единиц массы (или а.е.м.), каждая из которых равна 1/12 массы атома углерода-12. Тогда если масса моля углерода-12 равна 12 г и масса среднего атома серы больше массы атома углерода-12 в таком соотношении:
то моль атомов серы должен обладать такой массой:
Как удобно! Знание того, что моль элемента имеет ту же массу в граммах, что и атомная масса этого элемента в атомных единицах массы, еще пригодится в ваших вычислениях. Атомную массу любого элемента в атомных единицах массы можно узнать из любой таблицы Менделеева. Например, масса моля кремния равна 28,09 г, моля натрия равна 22,99 г и т.д. И в каждом из этих молей содержится 6,022·1023 атомов.
Теперь вы сможете определить количество атомов в алмазе, который является одним из твердых состояний углерода (с атомной массой, равной 12,01 а.е.м.). 12,01 г алмаза составляют 1 моль, поэтому для вычисления количества атомов в алмазе нужно определить количество молей в алмазе и умножить эту величину атомов в моле, т.е. на 6,022·1023 атомов.
Далеко не все тела состоят из атомов одного вида. Большинство материалов является составными, например, вода, в которой на каждый атом кислорода приходится два атома водорода (Н2O). В подобных случаях вместо атомной единицы массы следует использовать молекулярную массу, которая также основана на атомных единицах массы. Например, молекулярная масса воды равна 18,0153 а.е.м., так что масса одного моля молекул воды равна 18,0153 г.
Выводим закон идеального газа
Описание поведения газообразных состояний так, как того требует физика, начинается тогда, когда мы перейдем на уровень атомов и молекул. Как используется понятие “моль” для описания физических процессов при нагревании газов? Оказывается, что поведение разных газов можно связать друг с другом с помощью таких уже известных нам физических понятий, как моли, температура, давление и объем. Эта связь не совсем точна для реальных газов в природе, но очень хорошо описывает поведение идеальных газов. (Идеальный газ — это газ, в котором взаимодействие молекул сводится к парным столкновениям, причем время межмолекулярного столкновения много меньше среднего времени между столкновениями. — Примеч. ред.) Однако некоторые реальные газы, например гелий, с очень хорошей точностью описываются как идеальные, и именно они образуют надежный экспериментальный “оплот” термодинамики.
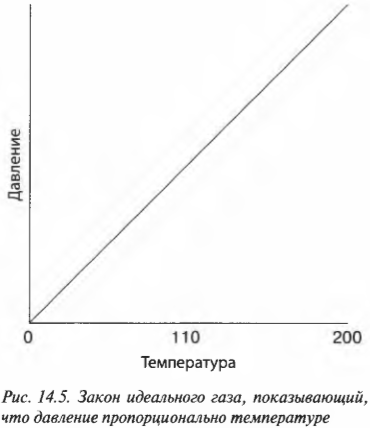
Экспериментально доказано, что если нагревать газ, сохраняя его объем неизменным, то, как показано на рис. 14.5, давление газа будет расти линейно. Другими словами, при постоянном объеме:
где \( T \) — температура, измеренная в кельвинах, а \( P \) — давление.
Если менять объем, то можно заметить, что давление будет ему обратно пропорционально, т.е. при увеличении объема газа в два раза, давление этого газа в два раза уменьшится:
С другой стороны, когда объем и температура идеального газа постоянны, то давление пропорционально количеству имеющихся молей газа — при увеличении количества газа в два раза, давление удваивается. Если количество молей равно \( n \), то:
Вставив в формулу постоянную \( R \) (так называемую универсальную газовую постоянную, значение которой равно 8,31 Дж/(моль·К), получим закон идеального газа, связывающий друг с другом давление, объем, количество молей и температуру:
Поистине идеальными считаются газы, для которых выполняется данный закон идеального газа. С помощью этого закона можно предсказывать давление идеального газа, если знать его количество, температуру и занимаемый им объем.
Закон идеального газа можно выразить несколько по-другому, если использовать число Авогадро \( N_А \) (см. предыдущий раздел) и общее количество молекул \( N \):
Отношение \( R/N_А \) также называется постоянной Больцмана \( k \) и равно 1,38·10-23 Дж/К. С использованием этой константы закон идеального газа принимает такой вид:
Давление: пример использования закона идеального газа
Допустим, что имеется резервуар объемом 1 м3, заполненный 600 молями гелия (очень близкого к идеальному газу) при комнатной температуре в 27°С. Каким будет давление газа? Используя следующую форму уравнения идеального газа:
получим следующую формулу, в которую подставим численные значения:
Давление во все стенки сосуда равно 1,50·106 Н/м2. Обратите внимание на используемую единицу измерения давления, Н/м2. Эта единица измерения используется настолько широко, что имеет в системе СИ собственное название — паскаль, или Па. Атмосферное давление равно 1,013·105 Па. Кроме того, давление в одну атмосферу иногда указывают в единицах торр и 1 атмосфера = 760 торр. А в нашем примере давление равно 1,50·106 Па, или примерно 15 атмосфер.
Иногда приходится сталкиваться со специальным набором условий, применяемым к газам, которые называются нормальными условиями (или н.у.). Они соответствуют следующим физическим условиям: давление равно 1 атмосфере, т.е. 1,013·105 Па, а температура равна 0°С. С помощью закона идеального газа можно подсчитать, что в нормальных условиях 1 моль идеального газа занимает объем 2,24136·10-2 м3, или около 22,4 литра (1 литр равен 1·10-3 м3).
Закон Бойля-Мариотта и закон Шарля: альтернативные формулировки закона идеального газа
Закон идеального газа часто формулируют по-разному. Например, можно выразить отношение между давлением и объемом идеального газа до и после того, как одна из этих величин изменится при постоянной температуре:
Из этой формулы, выражающей закон Бойля-Мариотта, следует, что при прочих неизменных условиях произведение \( PV \) будет сохраняться.
Далее, если давление постоянно, то можно сказать, что:
Из этой формулы, выражающей закон Шарля, следует, что для идеального газа при прочих неизменных условиях будет сохраняться отношение \( V/T \).
Аналогично, если объем постоянен, то можно сказать, что:
Из этой формулы, выражающей закон Гей-Люссака, следует, что для идеального газа при прочих неизменных условиях будет сохраняться отношение \( P/T \).
Измерение давления воды и воздуха
Попробуем применить наши знания о давлении в повседневной жизни. Ну, давление под слоем жидкости, например воды, можно определить с помощью простой формулы:
P = pgh.
Здесь p — плотность жидкости, g — ускорение свободного падения под действием силы тяжести (9,8 м/с2), h — глубина, для которой вычисляется давление. Для воды p равна 1000 кг/м2, так что получается:
P = (10000,0)(9,8)h = 9800h.
С каждым метром глубины, на которую вы уходите под воду, давление увеличивается примерно на 9800 Па, или примерно на 1/10 атмосферы (о том, как преобразовывать друг в друга атмосферы и паскали, описывалось выше).
Эта формула правильна, пока плотность жидкости не меняется, т.е. для воздуха предсказать такое давление трудно, ведь плотность воздуха, как известно, меняется вплоть до безвоздушного пространства открытого космоса. Часто встречаются задачи по физике, в которых спрашивается, насколько поменяется давление воздуха, если подняться на ту или иную высоту. Другими словами, в этих задачах предлагается найти разность давлений для данной разности высот, на которых p постоянна.
Следим за молекулами идеального газа
Некоторые свойства молекул идеального газа можно изучать, как если бы эти молекулы мчались, как автомобили вокруг вас. Например, среднюю кинетическую энергию для каждой молекулы можно вычислить с помощью очень простой формулы:
где \( k \) — постоянная Больцмана, равная 1,38·10-23 Дж/К, а \( T \) — температура. А так как можно получить массу каждой молекулы, если знать, для какого газа ведется расчет (см. выше), то можно вычислить скорости молекул при различных температурах.
Вычисляем скорость молекул воздуха
Представьте, что в один прекрасный весенний день вы находитесь с друзьями на пикнике. У вас прекрасное угощение: картофельный салат, бутерброды и напитки. Но спустя некоторое время вы вспоминаете о физике, заваливаетесь на спину и начинаете смотреть в небо. Физика на пикнике, что может быть скучнее? Вот уж нет. Физика присутствует всюду: в любом месте и в любое время, даже если прямые признаки ее присутствия совсем не очевидны.
Даже если снующие вокруг молекулы воздуха не видны, с помощью законов физики вы легко сможете вычислить их среднюю скорость. Все, что вам нужно, — это калькулятор и термометр. Допустим, что измеренная температура воздуха оказалась примерно равной 28°С, или 301 К (о том, как преобразовывать друг в друга градусы Цельсия и Кельвина, можно узнать в главе 13). Как известно, среднюю кинетическую энергию молекул, находящихся в воздухе, можно вычислять с помощью формулы:
Остается подставить в нее численные значения:
Итак, “среднестатистическая” молекула обладает кинетической энергией, равной 6,23·10-21 Дж. Однако молекулы очень малы — так какие же скорости будут соответствовать этому значению? Как можно узнать в главе 8:
где \( m \) и \( v \) — это, соответственно, масса и скорость, тогда:
Воздух в основном состоит из молекул азота N2 (около 78%) и молекул кислорода O2 (около 21%). Без большой утраты точности предположим, что воздух в основном состоит из молекул азота. Молекула азота имеет массу, примерно равную 4,65·10-26 кг (которую вы можете вычислить сами, зная молекулярную массу азота и затем поделив ее на число \( N_А \)). Подставив в последнюю формулу числа, получим:
Ух! Только себе представьте себе, что такое громадное количество “малышей” каждую секунду врезается в вас со скоростью 1861 км/ч! Хорошо, что молекулы такие маленькие. Представьте, если бы каждая молекула воздуха весила примерно килограмм.
Вычисляем внутреннюю энергию идеального газа
Атомы и молекулы обладают очень малой массой, но их в газах очень много, а поскольку все они обладают кинетической энергией, то можно определить их общую кинетическую энергию или ту часть внутренней энергии газа, которая состоит из энергии движения его молекул. Итак, какой кинетической энергией обладает известное количество газа? Каждая молекула обладает средней кинетической энергией:
Чтобы получить общую кинетическую энергию, надо среднюю кинетическую энергию умножить на количество имеющихся молекул, равное \( nN_А \), где \( n \) — это количество молей:
Здесь \( N_Аk \) равняется \( R \), т.е. универсальной газовой постоянной (см. ранее в этой главе), поэтому прежняя формула принимает вид:
Итак, 600 молей гелия при температуре 27°С обладают следующей внутренней энергией, которая связана с тепловым движением молекул:
Это чуть больше половины килокалории! Такого рода единицу измерения условной энергетической ценности продуктов питания (ккал) можно найти на их упаковках.






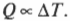
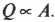
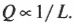
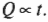
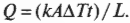

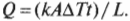
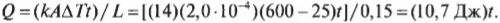
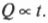
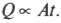
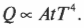
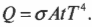
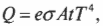
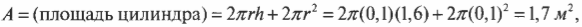
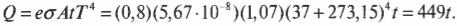
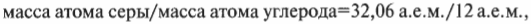
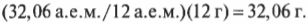
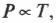
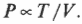
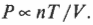
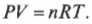
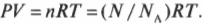
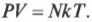
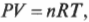
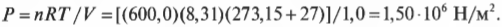
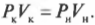
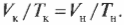
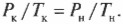
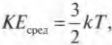
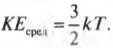
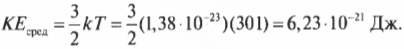
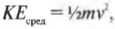
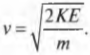
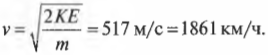
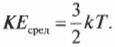
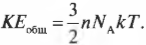
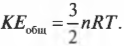
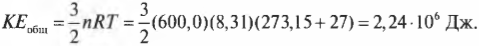
Добавить комментарий
[…] Источник […]