Механические колебания и волны

1. Механические колебания — точно или приблизительно повторяющееся движение, при котором тело смещается относительно положения равновесия, отклоняясь от него то в одну, то в другую сторону.

Для того чтобы возникли и совершались механические колебания необходима колебательная система. В механике изучаются две колебательные систем: математический и пружинный маятники.

2. Колебательная система — математический маятник — представляет собой тело, подвешенное на нити, размеры которого много меньше длины нити. Кроме того, нить математического маятника нерастяжима и не имеет массы, вся масса такого маятника сосредоточена в подвешенном к нити грузе.

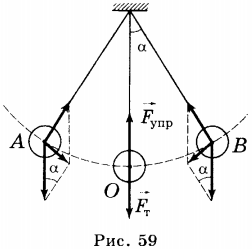
В положении равновесия (рис. 59) на маятник действуют противоположно направленные сила тяжести \( \vec{F}_т \) и сила упругости \( \vec{F}_у \). Их равнодействующая равна нулю.

При отклонении маятника от положения равновесия вправо эти две силы направлены
под углом друг к другу, и их равнодействующая \( \vec{F} \) уже не равна нулю. Под действием равнодействующей силы \( \vec{F} \) маятник начнёт двигаться к положению равновесия. Поскольку груз обладает инертностью, то он пройдет положение равновесия и отклонится от него в другую сторону. Дойдя до крайнего левого положения, маятник под действием равнодействующей сил тяжести и упругости начнёт двигаться к положению равновесия. Пройдя его, он опять отклонится вправо. Процесс будет повторяться. Таким образом, в процессе колебаний изменяются смещение, скорость, действующая на него сила, ускорение маятника. При этом ускорение маятника прямо пропорционально его смещению и направлено в противоположную сторону. Для математического маятника это равенство имеет вид: \( \vec{a}=-\frac{\vec{g}}{l} \), где \( l \) — длина нити маятника.

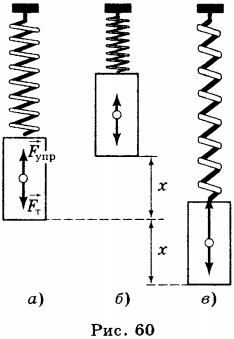
3. Колебательная система — пружинный маятник — это груз, прикреплённый к пружине (рис. 60). Считают, что масса пружины маятника мала по сравнению с массой груза, деформацией тела пренебрегают по сравнению с деформацией пружины. Кроме того, полагают, что деформация пружины подчиняется закону Гука \( (F=-kx) \).

В состоянии равновесия пружина не деформирована (рис. 60), и на груз в горизонтальном направлении силы не действуют.

При выведении груза из состояния равновесия, на него будет действовать сила упругости
пружины \( \vec{F}_у \), прямо пропорциональная её удлинению и направленная к положению равновесия. Под действием этой силы груз начнёт двигаться к положению равновесия.

Благодаря инертности груз пройдёт положение равновесия. Пружина сожмется, и в ней опять возникнет сила упругости. Дойдя до крайнего левого положения, груз остановится, а затем под действием силы упругости начнёт возвращаться в положение равновесия. Пройдя его, он отклонится вправо, и процесс повторится. Пружинный маятник будет совершать свободные колебания относительно положения равновесия.

Колебания, которые маятник совершает за счет однократно переданной ему энергии, называются свободными.

В соответствии со вторым законом Ньютона \( F=ma \). С другой стороны, \( F=-kx \). Откуда \( ma=-kx \), \( a=-\frac{kx}{m} \). Таким образом, ускорение колебаний пружинного маятника, так же как и математического, прямо пропорционально его смещению с обратным знаком. Такие колебания называются гармоническими.

4. Отклонение маятника от положения равновесия называется смещением \( (x) \), а максимальное отклонение — амплитудой колебаний \( (A\, или \,x_0) \).

Движение маятника от т. А до т. В и обратно до т. А называется полным колебанием. Время, за которое маятник совершает одно полное колебание, называется периодом колебаний (см. рис. 59). Период обозначают буквой \( T \) и измеряют в секундах.

Если маятник совершил за 4 секунды 8 полных колебаний, то его период равен 0,5 с.

Величину, обратную периоду, называют частотой колебаний. Частоту обозначают буквой \( \nu \). По определению \( \nu=1/T \). Единица частоты 1 герц (Гц).

Один герц — это частота таких колебаний, при которых за 1 секунду совершается одно полное колебание: 1 Гц = 1 с^-1.

Если частота колебаний 5 Гц, то это означает, что за 1 секунду совершается 5 полных колебаний. Период таких колебаний равен: \( T \) = 0,2 с.

Период колебаний математического и пружинного маятников зависит от характеристик этих систем.

Формула периода колебаний математического маятника: \( T=2\pi\sqrt{\frac{l}{g}} \), где \( l \) — длина нити маятника, \( g \) — ускорение свободного падения.

Формула периода колебаний пружинного маятника имеет вид: \( T=2\pi\sqrt{\frac{m}{k}} \), где \( m \) — масса груза, \( k \) — коэффициент жёсткости пружины.

5. Основной задачей механики является определение положения тела, т.е. его координаты, в любой момент времени. Эта задача может быть решена, если известно уравнение, выражающее зависимость координаты тела от времени. Для гармонического колебания это уравнение имеет вид: \( x=x_0\!\cos\!\omega t \) или \( x=x_0\!\sin\!\omega t \), в зависимости от того, какой была координата (смещение) маятника в начальный момент времени. В том случае, если маятник в начальный момент времени был отклонен от положения равновесия (начальная координата не равна нулю), изменение координаты происходит по закону косинуса; если он начал двигаться из положения равновесия \( (x_0=0) \), то изменение координаты (смещения) подчиняется закону синуса. В записанном уравнении координаты \( \omega \) — циклическая частота колебаний. Циклическая частота колебаний равна числу колебаний за \( 2\pi \) секунд: \( \omega=2\pi\sqrt{\frac{2\pi}{T}} \). Циклическая частота, так же как и период колебаний маятника, зависит от параметров колебательной системы: \( \omega=2\pi\sqrt{\frac{g}{l}} \) и \( \omega=2\pi\sqrt{\frac{k}{m}} \).

6. При выведении маятника из положения равновесия ему сообщают потенциальную энергию. За счет этой энергии происходит движение маятника к положению равновесия. В процессе движения потенциальная энергия переходит в кинетическую. В положении равновесия потенциальная энергия маятника равна нулю, а его кинетическая энергия максимальна. При движении маятника влево кинетическая энергия переходит в потенциальную; в крайнем левом положении кинетическая энергия равна нулю, а потенциальная — максимальна. В отсутствие трения полная механическая энергия маятника сохраняется.

7. При наличии сопротивления воздуха сообщенная маятнику энергия расходуется на совершение работы против силы трения, энергия маятника постоянно уменьшается, и колебания со временем прекращаются. Говорят, что они затухают.

Таким образом, реальные свободные колебания маятника всегда затухающие.

Для получения незатухающих колебаний необходимо компенсировать потери энергии. Это можно сделать, действуя на маятник с некоторой периодической силой. В этом случае колебания происходят под действием внешней силы и становятся вынужденными. Работа этой силы и восполняет потери энергии, вызванные трением. Эти колебания будут вынужденными.

Вынужденные колебания — это колебания, происходящие под действием внешней, периодически изменяющейся силы. Частота вынужденных колебаний равна частоте изменения действующей на тело силы. Частота вынужденных колебаний равна частоте изменения внешней силы.

8. Если подвесить к верёвке, прикреплённой к стойке, несколько маятников разной длины и привести в колебания один из них, то и другие маятники начнут колебаться. Частота их колебаний будет равна частоте колебаний маятника, возбудившего колебании. При этом с наибольшей амплитудой будет колебаться маятник, длина которого равна длине этого маятника. Следовательно, наибольшую амплитуду колебаний имеет маятник, собственная частота колебаний которого совпадает с частотой вынуждающей силы. Явление, которое наблюдается в этом случае, называется резонансом.

Резонанс — явление резкого возрастания амплитуды вынужденных колебаний тела, наступающего при равенстве частоты изменения внешней силы и частоты собственных колебаний тела.

Явление резонанса необходимо учитывать в практике. Известны случаи, когда вследствие резонанса разваливался на части самолёт в воздухе, ломались гребные винты у судов, рушились железнодорожные рельсы. Во всех этих случаях с резонансом приходится бороться, изменяя либо собственную частоту системы, либо частоту силы, вызывающей колебания.

9. Механической волной называется процесс распространения механических колебаний в среде.

Если закрепить конец шнура, слегка натянуть его и сместить свободный конец вверх, а затем вниз, т.е. привести его в колебания, то но шнуру «побежит» волна. Каждая точка
шнура будет совершать вынужденные колебания с частотой внешней силы, но с некоторым опозданием. При распространении колебаний по шнуру волна «бежит» в горизонтальном направлении, а колебания частицы совершают в вертикальном направлении.

Волны, направление распространения которых перпендикулярно направлению колебаний частиц среды, называются поперечными.

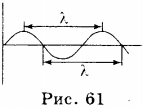
Поперечные волны представляют собой чередование горбов и впадин (рис. 61).

Расстояние между двумя ближайшими горбами или впадинами называется длиной волны.

Длина волны обозначается букой \( \lambda \) и измеряется в метрах.

На расстояние, равное длине волны, волна распространяется за время, равное периоду колебаний.

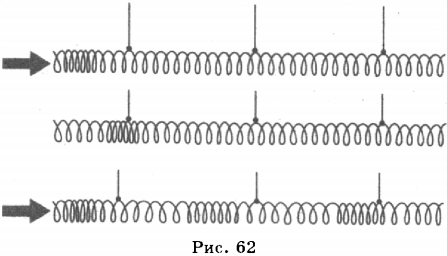
10. Если закрепить один конец длинной пружины, а по другому ударить, то возникшее на конце пружины сгущение витков «побежит» по ней (рис. 62). В этом случае волна представляет собой распространение сгущений и разрежений. Частицы среды при этом совершают колебания вдоль направления распространения волны. Такие волны называют продольными.

Продольные волны — это такие, направление распространения которых совпадает с направлением колебаний частиц среды.

11. Волновое движение имеет следующие особенности:

механические волны образуются благодаря инертности частиц среды и взаимодействию между ними, проявляющемуся в существовании сил упругости;
каждая частица среды совершает вынужденные колебания такие же, что и первая частица, приведенная в колебания, частота которых равна частоте внешней силы. Период колебаний всех частиц одинаков;
колебание каждой частицы происходит с запаздыванием, которое обусловлено её инертностью. Это запаздывание тем больше, чем дальше находится частица от источника колебаний;
вместе с волной не переносится вещество, переносится энергия.

12. Распространение продольных волн связано с изменением объёма тела. Они могут распространяться как в твёрдых, так и в жидких и газообразных телах, поскольку во всех этих телах при изменении объёма возникают силы упругости.

Распространение поперечных волн связано главным образом с изменением формы тела. В газах и жидкостях при изменении формы силы упругости не возникают, поэтому поперечные волны в них распространяться не могут. Поперечные волны распространяются только в твёрдых телах.

Примером волнового движения в твёрдом теле является распространение колебаний во время землетрясений. От центра землетрясения распространяются как продольные, так и поперечные волны. Сейсмическая станция принимает сначала продольные волны, а затем поперечные, т.к. скорость последних меньше. Если известны скорости поперечной и продольной волн и измерен промежуток времени между их приходом, то можно определить расстояние от центра землетрясения до станции.

13. Скоростью волны считается скорость перемещения гребня или впадины в поперечной волне, сгущения или разрежения в продольной волне.

За время, равное периоду колебаний \( (T) \), гребень или впадина перемещаются на расстояние, равное длине волны \( (\lambda) \). Следовательно, скорость волны \( (v) \) равна: \( v=\frac{\lambda}{T} \).

Поскольку \( T=\frac{1}{v} \), то формулу для скорости можно записать иначе: \( v=\lambda \nu \).

Скорость волны равна произведению длины волны и частоты колебаний.

14. Колебания, происходящие с частотой от 16 Гц до 20 000 Гц, являются звуковыми колебаниями. Для распространения звуковых колебаний, так же как и любых механических колебаний, необходима упругая среда.

Скорость звука можно определить, если известны расстояние от источника звука \( S \) и время распространения звука \( t \): \( v=\frac{S}{t} \). Скорость звука неодинакова в разных средах и зависит от температуры среды.

Физиологическим характеристикам звука (громкости, высоте тона) соответствуют физические характеристики. Громкость звука определяется амплитудой колебаний. Чем она больше, тем громче звук. Звук тем выше, чем больше частота колебаний.

Содержание

ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
Ответы

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Какой путь пройдёт груз математического маятника за 10 полных колебаний, если амплитуда колебаний равна 3 см?

1) 30 см
2) 60 см
3) 90 см
4) 120 см

2. Маятник совершает 20 полных колебаний за 10 с. Чему равна частота колебаний маятника?

1) 20 Гц
2) 2 Гц
3) 1 Гц
4) 0,5 Гц

3. Во сколько раз надо изменить массу груза пружинного маятника, чтобы период колебаний увеличился в 9 раз?

1) увеличить в 3 раза
2) уменьшить в 9 раз
3) уменьшить в 81 раз
4) увеличить в 81 раз

4. Массу груза математического маятника, совершающего гармонические колебания, увеличили в 9 раз. При этом период колебаний

1) увеличился в 3 раза
2) увеличился в 9 раз
3) уменьшился в 3 раза
4) не изменился

5. Если перенести математический маятник с Земли на Марс, то

1) частота колебаний не изменится
2) частота колебаний увеличится
3) частота колебаний уменьшится
4) маятник не будет колебаться

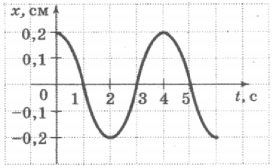
6. На рисунке представлен график колебаний математического маятника. Период колебаний маятника равен

1) 1 с
2) 2 с
3) 3 с
4) 4 с

7. Период колебаний частиц в волне можно вычислить по формуле

1) \( T=\frac{\nu}{\lambda} \)
2) \( T=\frac{\lambda}{\nu} \)
3) \( T=\lambda\nu \)
4) \( T=v\nu \)

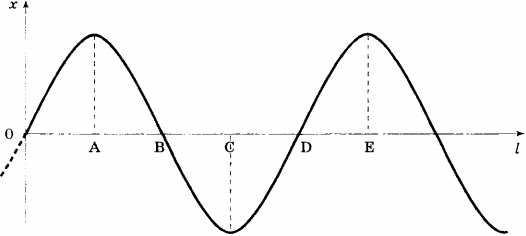
8. На рисунке показан график волны, бегущей вдоль упругого шнура, в некоторый момент времени. Длина волны равна расстоянию

1) ВС
2) BD
3) BE
4) OD

9. Сравните громкость звука и высоту тона двух звуковых колебаний, если для первого колебания: амплитуда \( A_1 \) = 2 мм, частота \( \nu_1 \) = 500 Гц, для второго колебания: \( A_2 \) = 4 мм, частота \( \nu_w \) = 300 Гц.

1) громкость первого звука больше, чем второго, а высота тона меньше
2) и громкость, и высота тона первого звука больше, чем второго
3) и громкость и высота тона первого звука, меньше, чем второго
4) громкость первого звука меньше, чем второго, а высота тона больше

10. Волна частотой 3 Гц распространяется в среде со скоростью 6 м/с. Длина волны равна

1) 18 м
2) 2 м
3) 1 м
4) 0,5 м

11. Математический маятник отвели в сторону и отпустили. Как будут изменяться значения величин, характеризующих колебания маятника при его движении к положению равновесия. Для каждой величины из первого столбца подберите соответствующее характеру её изменения слово из второго столбца. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры могут повторяться.

ВЕЛИЧИНЫ
A) смещение
Б) скорость
B) потенциальная энергия

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется

12. Среди приведённых ниже положений укажите два правильных и запишите их номера в таблице.

1) Звук распространяется только в воздухе.
2) Колебания, частота которых больше 20 000 Гц, называются ультразвуком.
3) Инфразвук — колебания, частота которых больше 16 Гц.
4) Эхо — явление многократного отражения звуковых волн от преград.
5) Звуковые волны — поперечные.