Глава 5. Толкаем, чтобы привести в действие: сила

В этой главе…
- Прилагаем силу
- Открываем три закона Ньютона
- Используем векторы силы для законов Ньютона
В этой главе описываются знаменитые три закона Ньютона. Вероятно, вам уже приходилось встречаться с разными формулировками этих законов, например “всякому действию всегда есть равное ему противодействие”. Эта формулировка не совсем верна, поскольку “всякой силе всегда есть равная ей противоположная сила”. В этой главе будут прояснены различия между этими формулировками. Законы Ньютона в данной главе используются для фокусировки вашего внимания на силах и их влиянии на окружающий нас мир.
Содержание
Форсируем тему
В окружающем нас мире нельзя избежать встречи с силами: силы используются для открытия двери, нажатия клавиш клавиатуры, управления автомобилем, подъема по ступенькам лестницы к Статуе Свободы, вытаскивания кошелька из кармана, разговора и даже для дыхания. Силы незримо присутствует всюду: во время пешеходной прогулки, катании на коньках, пережевывании хот-дога, открывании бутылки или моргании ресниц вашей ненаглядной спутницы. Сила неразрывно связана с движением объектов, а физика помогает понять, как эта связь работает.
Сила — это на самом деле довольно забавная тема. Как и другие физические темы, она кажется сложной только до настоящего знакомства с ней. Как наши старые “друзья”, перемещение, скорость и ускорение (см. главы 3 и 4), сила является вектором, т.е. имеет величину и направление.
Сэр Исаак Ньютон первым включил силу, массу и ускорение в одно уравнение в XVII веке. (Помните исторический анекдот с падением яблока на его голову, в результате чего он якобы придумал, как математически описать силу тяготения. Подробнее об этом рассказывается в главе 6, где Ньютон также является одним из основных действующих лиц.)
Законы Ньютона и скорость света
Законы Ньютона были пересмотрены Альбертом Эйнштейном в его теории относительности. В ней было показано, что законы Ньютона не выполняются для движения со скоростью, близкой к скорости света. Основная идея теории относительности заключается в том, что скорость света является наибольшей возможной скоростью. Это значит, что любое взаимодействие может происходить только с этой или меньшей скоростью. Следовательно, при приближении к этой скорости нужно учитывать изменяющийся характер взаимодействия; Например, измерение длины ракеты, движущейся со скоростью света, будет отличаться от измерения длины неподвижной ракеты. Как будет показано в главе 21, теория относительности Эйнштейна в значительной степени изменила представленный Ньютоном взгляд на мир и его законы.
Как часто происходит со многими физическими открытиями, Ньютон сначала внимательно наблюдал за поведением объектов, мысленно моделировал его, а затем выразил в математической форме. Зная основные сведения о векторах (которые изложены в главе 4), эта математика не вызовет у вас никаких трудностей.
Ньютон описал свою модель с помощью трех утверждений, которые теперь называются законами Ньютона. Однако нужно помнить, что на самом деле это не окончательные “законы природы”, ведь физики могут создавать лишь модели природы, которые часто впоследствии пересматриваются и уточняются.
Первый закон Ньютона
Барабанную дробь, пожалуйста! Законы Ньютона описывают силы и движение, а его первый закон гласит: “Объект находится в состоянии равновесия или прямолинейном движении с постоянной скоростью, если не подвергается внешнему воздействию”. Нужен перевод? Если вы не прилагаете силу к объекту в покое или “постоянном” движении, то он останется в покое или таком же движении по прямой. Причем вечно!
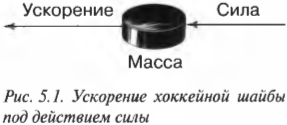
Например, при игре в хоккей шайба после удара движется к воротам по прямой, скользя по льду почти без трения. В случае удачи соперник не сможет зацепить шайбу своей клюшкой, т.е. не сможет изменить “постоянное” движение шайбы по прямой (и воспрепятствовать голу).
В повседневной жизни объекты не движутся так беспрепятственно, как в случае с шайбой на льду. Большинство окружающих нас объектов испытывает силу трения. Например, при скольжении кофейной чашки по гладкому столу она постепенно замедляет свое скольжение и останавливается (иногда с проливанием кофе не стоит чересчур упражняться, ибо вы рискуете испачкаться или ошпариться горячим кофе). Это совсем не значит, что первый закон Ньютона неверен. Наоборот, именно сила трения принуждает чашку изменить свое движение и остановиться.
Выражение “если не прилагать никакого действия к постоянно движущемуся объекту, он будет двигаться вечно” выглядит так же ужасно, как идея “вечного двигателя”. Однако полностью избавиться от внешнего воздействия сил невозможно, даже если объект находится в межзвездном пространстве. Даже на объекты в самых далеких уголках космоса оказывает воздействие (пусть даже очень слабое) масса других объектов Вселенной. А это значит, что на любое движение всегда оказывается внешнее воздействие, потому вечное постоянное движение в принципе невозможно.
Первый закон Ньютона утверждает лишь то, что единственным способом изменения движения является приложение внешней силы. Иначе говоря, сила является причиной движения. Кроме того, он гласит, что движущийся объект стремится оставаться в движении, что приводит к идее инерции.
Поддерживаем движение: инерция и масса
Инерция — это естественная тенденция объекта оставаться в покое или в движении с постоянной скоростью вдоль прямой линии. Инерция вызвана массой, а масса объекта является мерой инерции. Чтобы привести объект в движение, т.е. изменить его текущее состояние движения, необходимо приложить силу для преодоления инерции.
Представьте себе причал с маленькой шлюпкой и большим танкером с нефтью. Если попробовать толкнуть их ногой, то поведение этих судов будет разным. Шлюпка заскользит по водной глади, а танкер едва “вздрогнет” (да и для этого потребуется невероятно сильный толчок!). Дело в том, что они обладают совершенно разной массой и потому разной инерцией. В ответ на одинаковую силу объект с малой массой (и малой инерцией) ускорится в большей мере, чем объект с малой массой и большей инерцией.
Инерция, т.е. тенденция массы сохранять неизменность текущего состояния движения, иногда может представлять проблему. Например, в рефрижераторе тяжелые туши мороженного мяса подвешены к потолку кузова. Если рефрижератор войдет в крутой поворот на большой скорости, то туши по инерции начнут раскачиваться, как маятники, и их трудно будет остановить. Часто неопытные водители не учитывают инерцию туш мяса, и это приводит к печальным последствиям, например к опрокидыванию машины.
Поскольку масса обладает инерцией, то она сопротивляется изменению движения. Именно поэтому нам приходится прилагать силу для ускорения своего движения. Масса связывает силу и ускорение.
Измеряем массу
В разных системах измерения физических величин для указания массы (а значит, и инерции) используются разные единицы. В системе СГС используется грамм, а в системе СИ — килограмм, который содержит 1000 грамм.
А какая единица используется в Английской системе мер на основе фута-фунта- дюйма? Наберитесь мужества: в ней используется единица “слаг”, которая эквивалентна 14,5939 килограмма.
Учтите, что масса не равна весу. Масса — это мера инерции, а вес — это сила, которую оказывает сила притяжения Земли, измеренная на ее поверхности. Например, в Английской системе мер на основе фута-фунта-дюйма слаг имеет вес около 32 фунтов.
Леди и джентльмены, встречайте второй закон Ньютона!
Первый закон Ньютона очень и очень серьезен, но не выражается в математической формулировке, которая так необходима физикам. Потому Ньютон предложил свой второй закон: “если результирующая сила \( \sum\!F \) действует на объект массы \( m \), то ускорение \( a \) объекта можно вычислить по формуле \( \sum\!F=ma \)”. В “переводе” это значит: сила равна массе, умноженной на ускорение. Символ \( \sum \) означает суммирование, а значит, точнее говоря, закон гласит: суммарная, или результирующая, сила равна массе, умноженной на ускорение. (С точки зрения физики процесса, а не формальной математики, ускорение является следствием действия силы, а не наоборот. Потому логичнее было бы сформулировать второй закон Ньютона так: \( a=\sum\!F/m \), т.е. ускорение объекта прямо пропорционально результирующей силе на него и обратно пропорционально массе.)
Согласно первому закону Ньютона, движущееся тело остается в прямолинейном движении с постоянной скоростью, если на него не действует сила. Получается, что на самом деле он является частным случаем второго закона Ньютона, когда \( \sum\!F=0 \). Ведь в таком случае ускорение равняется нулю, о чем говорится в первом законе Ньютона. Взгляните на хоккейную шайбу на рис. 5.1: шайба ускоряется, пока на нее действует сила.
Попробуйте применить уже полученные знания физики в этом примере. Действительно, если даже на долю секунды с помощью клюшки применить силу к шайбе, то она ускорится и, несомненно, попадет в сетку! В данном примере сила применена к клюшке с определенной массой, которая ускорилась и придала это ускорение шайбе.
Чему равно это ускорение? Эта величина зависит не только от единиц измерения массы, но и от единиц измерения силы.
Выбираем единицы измерения силы
Итак, в каких единицах выражается сила? Поскольку \( \sum\!F=ma \), то, например, в системе СИ сила выражается следующим образом:
Поскольку большинство людей считают эту единицу чересчур сложной, то в системе СИ используется специальная единица — ньютон (угадайте, в честь кого?). Сокращенно “ньютон” записывается как Н. В системе СГС сила выражается следующим образом:
Это тоже довольно неуклюжая единица, и в системе СГС для силы предложено использовать особую единицу — дина, причем 1 ньютон равен 105 динам.
Еще проще выражается единица сила в Английской системе мер на основе фута-фунта-дюйма-секунды — фунт, который выражается следующим образом:
и равен 4,48 ньютонам.
Вычисляем результирующую силу
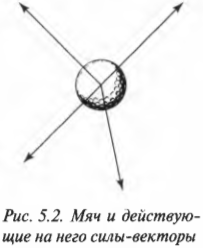
В большинстве учебников вместо полной записи \( \sum\!F=ma \) используется сокращенная — \( F=ma \), где под \( F \) подразумевается результирующая сила. Объект реагирует именно на результирующую силу, которая является суммой всех сил-векторов. Например, на рис. 5.2 показан мяч для игры в гольф и действующие на него силы. Как и в каком направлении будет двигаться мяч?
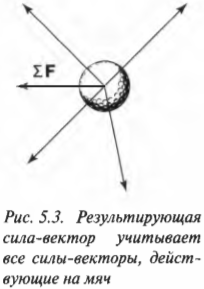
Поскольку во втором законе Ньютона говорится о результирующей силе, то задача упрощается. Все, что нужно сделать, так это сложить все силы-векторы для получения результирующей силы-вектора, как показано на рис. 5.3. Далее, для определения характера движения мяча нужно применить формулу \( \sum\!F=ma \).
Вычисляем перемещение по известному времени, массе и действующим силам
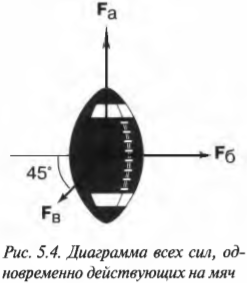
Допустим, что во время игры в мяч вы заинтересовались силами, действующими на мяч. Вот в одной из игровых ситуаций три игрока одновременно пытаются завладеть мячом и действуют на него тремя силами, как показано на рис. 5.4.
Схема на рис. 5.4 в физике называется диаграммой сил, действующих на тело. С ее помощью можно определить компоненты сил и результирующую силу.
Допустим, что с риском для жизни во имя науки вам удалось определить величины сил игроков:
Допустим, что масса мяча точно равна 1,0 кг. Вопрос звучит так: где будет мяч через 1 секунду? Вот те этапы, которые нужно пройти, чтобы вычислить перемещение мяча по известному времени движения и ускорению (которое еще нужно определить по известной массе и действующим силам), т.е. дать окончательный ответ на этот вопрос.
- Найти результирующую силу \( \sum\!F\) с помощью операции сложения векторов (подробное описание этой операции приводится в главе 4), складывая все силы, действующие на объект.
- Определить вектор ускорения по формуле \( \sum\!F=ma \).
- Вычислить пройденное расстояние за заданное время по формуле \( \mathbf{s}=\mathbf{v_0}(t_1-t_0)+{}^1\!/\!_2\mathbf{a}(t_1-t_0)^2 \) (см. главу 3, где подробно описывается эта формула).
Пора подставлять числа и доставать калькулятор. Итак, для связи силы, массы и ускорения нужно, прежде всего, определить результирующую силу. Для этого нужно разложить на компоненты все векторы-силы на рис. 5.4, а потом сложить компоненты, чтобы получить компоненты вектора результирующей силы (более подробно операция разбиения вектора на компоненты приводится в главе 4).
Компоненты векторов \( \mathbf{F_а} \) и \( \mathbf{F_б} \) можно определить очень легко, поскольку вектор \( \mathbf{F_а} \) ориентирован вдоль положительного направления оси Y, а вектор \( \mathbf{F_б} \) — вдоль положительного направления оси X. Это значит, что компоненты этих векторов выражаются следующим образом:
Компоненты вектора \( \mathbf{F_в} \) определяются немного сложнее, поскольку нам все придется их вычислить:
Вектор \( \mathbf{F_в} \) направлен под углом 45° по отношению к отрицательному направлению оси Х, как показано на рис. 5.4, и под углом \( \theta \) = 180°+45°=225° к положительному направлению оси X. Тогда компоненты вектора \( \mathbf{F_в} \) определяются следующим образом:
После подстановки чисел получим:
Обратите внимание на знак “минус” — оба компонента вектора \( \mathbf{F_в} \) отрицательные. Полученный результат всегда можно быстро проверить на непротиворечивость. Вектор \( \mathbf{F_в} \) направлен вниз и вправо, т.е. вдоль отрицательных направлений оси X и Y. Это значит, что оба компонента \( F_{вx} \) и \( F_{вy} \) должны быть отрицательными. Мне доводилось видеть людей, которые не могли правильно определить знак компонентов вектора, поскольку они не умели выполнять такую простую проверку непротиворечивости.
Всегда сравнивайте знаки компонентов векторов с фактическим направлением вдоль осей. Такая простая и быстрая проверка позволяет избежать многих потенциальных проблем.
Теперь нам известно, что:
И можно приступать к сложению векторов:
Итак, мы вычислили результирующую силу \( \sum\!\mathbf{F} \), которая равна (8 Н; 33 Н). Мы тем самым также определили направление движения мяча. На следующем этапе нужно определить ускорение на основании второго закона Ньютона:
Это означает, что:
Поскольку масса мяча равна 1 кг, то, подставляя это значение в предыдущую формулу, получим:
Неплохой прогресс: теперь вы знаете ускорение мяча. Теперь, чтобы узнать расстояние \( \mathbf{s} \), которое преодолеет мяч за 1 секунду, нужно использовать приведенную ниже формулу (из главы 3):
После подстановки чисел получим:
Ну что ж, совсем неплохо. После 1 секунды движения мяч продвинется на 8 метров вдоль положительного направления оси X и на 33 метра вдоль положительного направления оси Y. Достаньте секундомер, засеките промежуток времени длительностью 1 с и убедитесь, что мяч продвинулся на 8 метров вдоль горизонтальной линии и на 33 метра вдоль вертикальной линии. Вот вам еще один успешный физический эксперимент.
Вычисляем результирующую силу по известному времени и скорости
В предыдущем разделе перемещение объекта было вычислено по известному времени движения с постоянным ускорением. А как поступить, если нужно решить обратную задачу: как определить результирующую силу по известному времени и достигнутой скорости? Допустим, что нужно ускорить автомобиль от 0 до 60 миль в час за 10 секунд. Какую силу нужно приложить для этого? Сначала нужно преобразовать единицы измерения для более удобной работы со значениями скоростей, т.е. мили в час преобразовать в футы в секунды.
Обратите внимание на то, что часы и минуты в итоге сократились, а остались только мили и секунды. Теперь нужно выразить результат в футах в секунду:
Итак, за 10 секунд автомобиль разгонится до скорости около 88 футов в секунду. Если автомобиль весит около 2000 фунтов, то какая сила потребуется для такого ускорения? Сначала найдем величину самого ускорения на основе приведенной ниже формулы (более подробно она описывается в главе 3):
Подставляя числа, получим:
Итак, искомое ускорение равно 8,8 футов в секунду2. Согласно второму закону Ньютона:
Нам известно, что вес автомобиля равен 2000 фунтам. Чему равна масса автомобиля в другой системе единиц измерения, а именно в системе на основе фута-фунта-дюйма- секунды или в слагах? В этой системе единиц измерения нужно поделить вес на ускорение свободного падения под действием гравитации, т.е. 32,17 фута в секунду2 (эта величина получена после преобразования уже известной нам величины 9,8 метра в секунду2):
Теперь у нас есть все, что нужно для вычисления силы. Какая сила потребуется, чтобы автомобиль весом 62,17 слага двигался с ускорением 8,8 фута в секунду2. Нам нужно просто перемножить эти численные значения:
Итак, после округления до 2 значащих цифр получим, что для ускорения автомобиля до скорости 60 миль в час за 10 секунд потребуется сила 550 фунтов.
Учтите, что в данной задаче игнорируются такие особенности, как трение и наклон дороги. Более подробно эти вопросы рассматриваются в главе 6. Даже при движении по плоской поверхности без наклона трение может играть очень большую роль, и для ускорения автомобиля с учетом трения часто требуется приложить силу на 30% больше, чем 550 фунтов.
Торжественный финал: третий закон Ньютона
Этот закон движения особенно популярен среди борцов и инструкторов вождения автомобилей. Он гласит: сила действия одного объекта на другой равна по величине силе противодействия другого объекта, направленной в противоположную сторону.
Наиболее популярной формулировкой этого закона является следующая: “для любого действия всегда найдется равное ему и противоположное действие”. Однако физики предпочитают вместо неконкретного термина “действие” использовать более точный термин “сила”. Дело в том, что под действием часто подразумеваются совершенно разные явления, например характер голосования на избирательном участке или изменение температуры.
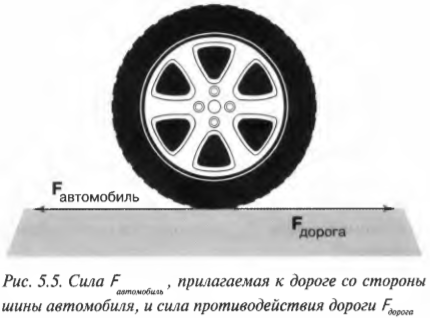
Допустим, что вы едете в автомобиле и для движения шина автомобиля должна прилагать силу к дороге (т.е. отталкиваться от нее), ибо иначе автомобиль не сможет двигаться. В таком случае дорога оказывает такую же силу на шину автомобиля, как показано на рис. 5.5.
Если бы силы действия автомобиля была больше силы противодействия, то шина проскальзывала бы по дороге, как при движении по льду.
У внимательного читателя может возникнуть вопрос: а почему дорога не движется в обратную сторону? На самом деле, верьте или нет, но третий закон Ньютона действует и дорога движется в обратную сторону. Действительно, шина автомобиля прилагает силу к поверхности дороги и приводит в движение Землю. Однако, учитывая, что масса Земли в 6⋅1021 раз больше массы автомобиля, это действие практически незаметно.
Учитываем трение
Когда хоккеист бьет клюшкой по шайбе, она ускоряется с места удара и ускоряется сам хоккеист. Если бы шайба имела массу 1000 кг (а не 105-185 г), то хоккеист, несомненно, ощутил бы это ускорение в гораздо большей мере. При таком нереальном соотношении масс хоккеиста и шайбы могло случиться так, что после удара шайба едва сдвинулась бы, а хоккеист заскользил бы в обратном направлении. (Более подробно такая ситуация описывается в части III.)
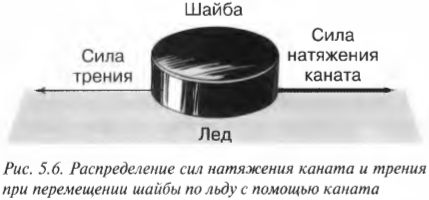
Допустим, что в данном фантасмагорическом примере по окончании игры нужно оттащить такую чудовищно тяжелую шайбу в сторону с помощью каната, как показано на рис. 5.6.
В физических задачах часто используются канаты, а также блоки, причем сила, с которой канат тянут с одного конца, равна силе сопротивления на другом конце каната.
В данном случае 1000-килограммовая шайба будет испытывать силу трения, пусть небольшую, но ощутимую. Итак, результирующая сила равна:
Поскольку сила натяжения каната \( F_{канат} \) больше силы трения \( F_{трение} \), то шайба начнет движение, причем ускоренное. Величину ускорения можно определить по известной формуле из второго закона Ньютона:
Одна часть силы натяжения каната \( F_{канат} \) расходуется на ускорение шайбы, а другая — на преодоление силы трения \( F_{трение} \):
Однако сила натяжения каната с одной стороны равна силе натяжения каната с другой, согласно третьему закону Ньютона.
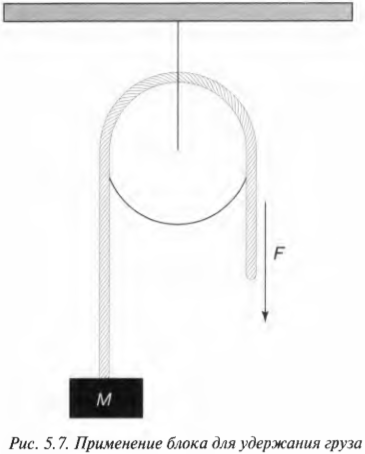
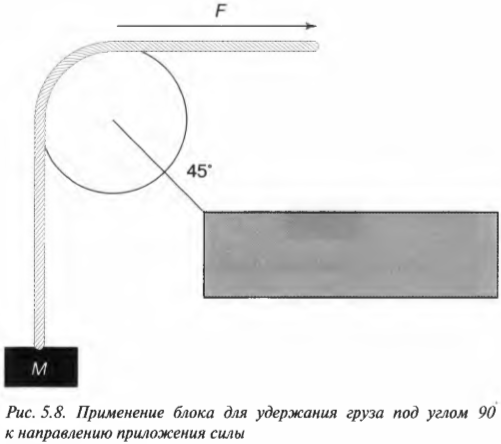
Рассмотрим теперь немного другую ситуацию, показанную на рис. 5.7. Допустим, что канат перекинут через блок и таким образом вам нужно поднять груз массы \( M \). Чтобы поднять груз, нужно преодолеть силу тяжести, которая действует на груз весом \( Mg \). Здесь \( g \) — это ускорение свободного падения под действием гравитации, равное 9,8 см/с2 (более подробно сила гравитации описывается в главе 6). На рис. 5.7 показана общая схема приложения силы к канату, необходимая для удержания груза.
Канат и блок используются не только для удержания груза, но и для изменения направления приложения силы. Сила прилагается вниз, а груз под ее действием движется вверх, поскольку канат перекинут через блок, где и происходит изменение направления действия силы. В данном случае, если сила натяжения каната \( F \) на свободном конце больше веса груза \( Mg \), то груз будет двигаться вверх с ускорением \( a \), согласно формуле:
Подсчитаем теперь силу, действующую на потолок, к которому прикреплен блок. Если блок находится в покое, то действующая на него результирующая сила \( \sum\!F=0 \). Это значит, что все силы, которые действуют на блок, в сумме дают 0.
На блок действуют две силы, направленные вниз: сила натяжения каната \( F \) на свободном конце и сила со стороны груза с весом \( Mg \), движущегося с ускорением \( a \). Согласно третьему закону Ньютона, они равны, и сумма двух сил, направленных вниз, равна \( 2F \). Поскольку действующая на блок результирующая сила \( \sum\!F=0 \), то действующая на блок и направленная вверх сила со стороны потолка тоже равна \( 2F \).
Ни одна сила не может прилагаться к объекту без возникновения равной по величине и противоположной по направлению силы (даже если какая-то ее часть порождается ускоренным движением объекта). В предыдущем примере канат и блок позволяют изменять направление действия силы. Однако такое изменение направления силы от \( -F \) до \( +F \) возможно за счет приложение силы \( 2F \) к блоку со стороны потолка.
Анализируем углы и величины в третьем законе Ньютона
Чтобы учесть углы приложения силы, нужно вспомнить правила сложения векторов. Взгляните на рис. 5.8, где с помощью каната и блока сила \( F \) прилагается для удержания в состоянии покоя груза с массой \( M \). Вопрос: с какой величиной и в каком направлении действует сила \( F_{опора} \) на опору блока?
Поскольку блок не движется, то действующая на него результирующая сила \( \sum\!F=0 \). Теперь нужно найти все силы, которые действуют на блок. Во-первых, нужно учесть силу тяжести \( \mathbf{F_{груз}}=M\mathbf{g} \), которая действует на груз. После разложения вектора этой силы на компоненты (подробнее об этом рассказывается в главе 4) получим (Y-компонента силы имеет отрицательный знак, поскольку она направлена вниз, т.е. вдоль отрицательного направления оси Y):
Теперь вычислим силу натяжения каната с другого конца \( F_{канат} \). Поскольку груз не движется, то сила натяжения каната на одном конце равна силе натяжения каната на другом конце. После разложения вектора силы натяжения каната на компоненты получим (Х-компонента силы имеет положительный знак, поскольку она направлена вправо, т.е. вдоль положительного направления оси X):
Теперь, чтобы найти результирующую силу, действующую на блок со стороны каната, нужно сложить компоненты сил \( F_{груз} \) и \( F_{канат} \):
Нам известно, что:
где \( F_{опора} \) — это сила, которая действует на опору блока.
Это значит, что:
Следовательно:
Глядя на рис. 5.8, можно легко проверить направление этого вектора. Действительно, блок должен противостоять силе тяжести груза (т.е. возникает сила противодействия, направленная вверх) и натяжению каната (т.е. возникает сила противодействия, направленная вправо).
Попробуем теперь определить величину и направление вектора силы \( F_{опора} \) (подробнее об этом рассказывается в главе 4). Величина этого вектора определяется по теореме Пифагора:
Обратите внимание на то, что здесь (как и в предыдущем примере) величина силы на опору блока больше величины каждой из сил по отдельности. Такова плата за изменение направления силы.
А в каком направлении действует сила \( F_{опора} \)? Из рис. 5.8 ясно, что сила \( F_{опора} \) должна быть направлена влево и вверх, а теперь попробуем проверить это предположение с помощью тригонометрии. Если \( \theta \) — это угол, под которым сила \( F_{опора} \) направлена по отношению к положительному направлению оси X, то Х-компонента силы \( F_{опора} \) имеет вид:
Следовательно:
Нам уже известно, что:
а также:
В итоге получим:
Нетрудно проверить, глядя на рис. 5.8, что найденное значение для направления силы на опору (-135) соответствует нашим предварительным оценкам и ожиданиям.
Если вы не уверены в правильности определения знаков сил, то всегда пробуйте проверить полученные значения с помощью визуального анализа нарисованной схемы распределения сил. Один рисунок порой стоит больше тысячи слов, особенно в физике!
Ищем состояние равновесия
В физике считается, что объект находится в состоянии равновесия, если его ускорение равно нулю, т.е. действующая на него результирующая сила равна 0. При этом объект необязательно должен находиться в покое — он может двигаться даже со скоростью 1000 километров в час, но без ускорения. Конечно, на объект в состоянии равновесия могут действовать самые разные силы, но их векторная сумма должна быть равна нулю.
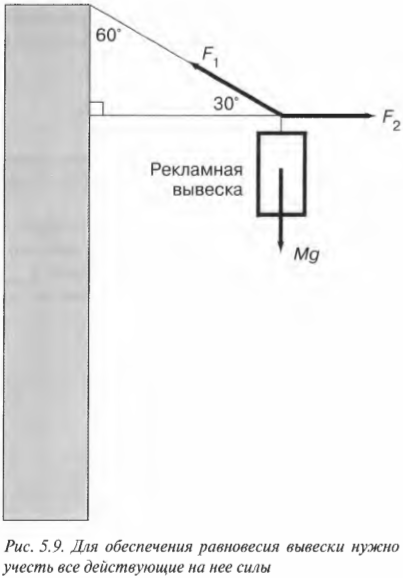
На рис. 5.9 показана схема распределения сил, действующих на рекламную вывеску перед магазином, которую вы собираетесь подвесить на проволоке, выдерживающей силу 15 Н.
Допустим, что вес вывески равен 8 Н. Хватит ли прочности проволоки для ее подвешивания? Иначе говоря, чему равна сила натяжения проволоки \( F_1 \) на этой схеме? Вывеска должна быть в состоянии равновесия, значит, результирующая сила на нее \( \sum\!F=0 \). Следовательно, весь вес вывески \( Mg \) должен быть уравновешен силой натяжения проволоки \( F_1 \).
В данном примере единственная направленная вверх сила — это Y-компонента силы \( F_1 \), как показано на рис. 5.9. Сила сопротивления \( F_2 \) горизонтальной балки направлена только по горизонтали, а потому не оказывает никакого влияния на вертикальную компоненту результирующей силы. С помощью навыков тригонометрии (более подробно базовые сведения по тригонометрии приводились в главе 4) можно определить Y-компоненту силы \( F_1 \):
Величина этой компоненты силы равна весу вывески:
Отсюда получаем натяжение проволоки:
Поскольку вес \( Mg \) вывески равен 8 Н, то получим
Ну и дела! Похоже, что проволока должна выдерживать силу 16 Н, а мы уже купили проволоку, выдерживающую всего 15 Н. Мораль сей задачи такова: нужно купить проволоку попрочнее!
Допустим, что мы купили более прочную проволоку и теперь интересуемся, достаточно ли прочна горизонтальная балка, чтобы выдержать силу сопротивления \( F_2 \), как показано на рис. 5.9. Какую прочность должна иметь балка, чтобы выдержать вес вывески? Иначе говоря, какую силу должна выдержать балка? На рис. 5.9 показаны только две горизонтальные силы: сила сопротивления балки \( F_2=F_{балка} \) и Х-компонента силы \( F_1 \). Нам уже известно, что \( F_1 \) = 16 Н. Теперь нам осталось только вычислить \( F_2 \). Для начала нужно определить Х-компоненту силы \( F_1 \) Глядя на рис. 5.9 и используя тригонометрию, получим:
Именно эта компонента силы натяжения проволоки равна силе сопротивления балки:
Это значит, что:
Итак, балка должна выдерживать силу около 14 Н.
Для подвешивания вывески весом около 8 Н потребуется проволока, выдерживающая силу около 16 Н, и балка, выдерживающая силу около 14 Н. Посмотрите снова на рис. 5.9: Y-компонента силы натяжения проволоки должна выдерживать вес груза. Такая прочность проволоки и балки нужна для того, чтобы изменить направление силы тяжести груза.






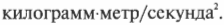
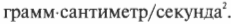
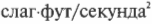
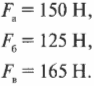
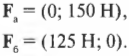
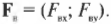
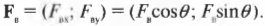
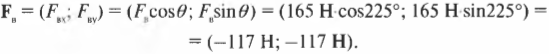

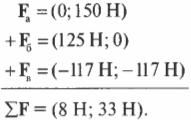
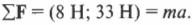
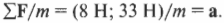
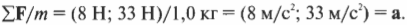
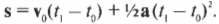
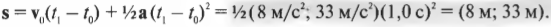

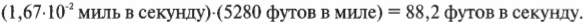
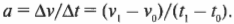
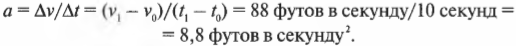
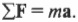
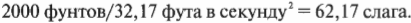
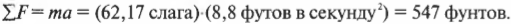

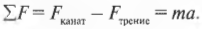
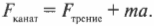
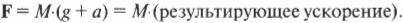
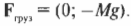
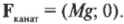
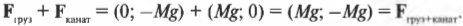

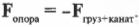
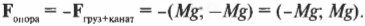
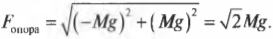
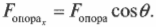
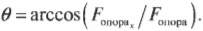
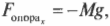
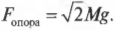
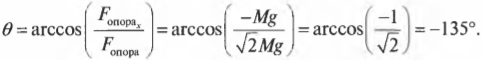
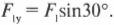
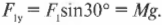
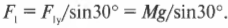
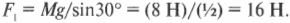
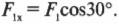
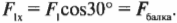
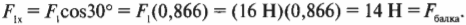
Добавить комментарий
[…] Источник […]
[…] Источник […]
Пока допирал с задачей с вывеской, дважды вывихнул себе мозг.
Почему 8 и 33 в задаче? Куда пропала 1/2? Невозмутимо опустилась? Авторы, не вводите в заблуждение, вы же сами учили пользоваться формулами.
куда делась 1/2 в последнем действии в главе «Вычисляем перемещение по известному времени, массе и действующим силам»?
Иначе говоря, сила является причиной движения.
Ньютон это не утверждал. Это утверждал Аристотель. Ньютон же утверждал, что сила является причиной изменения скорости движения!
Изменение скорости от нуля до, к примеру, десяти, это начало движения, а т.к Ньютон утверждал что сила является причиной изменения скорости движения, он так же и утверждал что сила является причиной движения.
В части «Учитываем трение» написано g=9.8см/с^2