Глава 2. Постигаем основы физики

В этой главе …
- Концепции физики и почему они так важны
- Учимся измерять (и решать уравнения)
- Оцениваем значимость и ошибку величин
- Освежаем свои знания алгебры и тригонометрии
Представьте себе, что вы бьетесь над решением почти неразрешимой физической задачи и пытаетесь найти подход к ней. Задача очень сложна и многим так и не поддалась. Внезапно в результате озарения все становится предельно ясным.
“Ну конечно, — говорите вы, — это же элементарно! Мяч в максимальной точке поднимется на высоту 9,8 м”.
Глядя на правильное решение задачи, преподаватель одобрительно кивнет головой, а вы, окрыленные успехом, с удвоенной силой приметесь за решение следующей задачи.
В физике, как и в любой другой области деятельности, заслуженный успех и слава достаются только в результате упорного труда. Не бойтесь работы, ведь цель оправдывает средства. По окончании чтения этого курса вы настолько овладеете предметом, что сможете решать те задачи, которые прежде казались вам просто неразрешимыми.
Эта глава начинается с описания некоторых базовых сведений и навыков, которые потребуются для освоения следующих глав. В ней описываются способы научных измерений, научные обозначения, базовые сведения по алгебре и тригонометрии, а также правила оценки значимости величин и точности полученных результатов. Полагаясь на эти твердые и незыблемые сведения, вы сможете овладеть всем другим материалом в этом курсе.
Содержание
Не бойтесь, это всего лишь физика
Многих от слова “физика” бросает в дрожь. Легко прийти в ужас, если представить себе физику, как нечто совершенно чуждое с высосанными из пальца абстрактными числами и правилами. Однако истина заключается в том, что физика призвана помочь нам понять реальный мир. Погружение в физику — это увлекательное путешествие, которое совершает человечество в попытке понять устройство мира.
Хотя может показаться справедливым и обратное утверждение, но нет никакой загадки в целях и методах физики: физика просто моделирует мир. Идея заключается в том, чтобы создать мысленные модели, описывающие поведение мира: как бруски скользят по наклонной плоскости, как образуются и светят звезды, как черные дыры захватывают свет, что происходит при столкновении автомобилей и т.п. В момент создания модели она совсем не содержит чисел, а только описывает самую суть явления. Например, звезда образуется из этого слоя, потом из того слоя, дальше возникает реакция, за ней другая и — бац, вот вам новая звезда!
По мере совершенствования модели ее описание становится количественным, и именно с этого момента изучения физики у учеников и студентов возникает большинство проблем. С изучением физики было бы меньше проблем, если бы можно было просто сказать: “Тележка, скатываясь по наклонной плоскости, движется все быстрее и быстрее”. Но для полного физического описания этого явления недостаточно сказать, что тележка движется быстрее, нужно сказать, насколько именно быстрее движется тележка.
Суть физики заключается в следующем: сделать наблюдение, создать модель для имитации явления, добавить математическое описание и — все! В таком случае вы сможете предсказывать развитие событий в реальном мире. Математика нужна, чтобы занять более уверенную позицию в реальном физическом мире и чтобы помочь в исследовании принципов и причин такого явления.
Учитесь у гения: не отгораживайтесь математикой от физики
Ричард Фейнман, лауреат Нобелевской премии по физике 1965 года “За фундаментальные работы по квантовой электродинамике, имевшие глубокие последствия для физики элементарных частиц*, в 1950-1960 годах заработал уникальную репутацию среди физиков. Свой метод исследования он объяснял так: нужно мысленно “на пальцах” описать задачу с указанием аналогии из реальной жизни, тогда как другие стремились сразу перейти к математическому описанию. Когда ему встречалась очень длинная теория с подозрительным результатом, он стремился найти какое-то физическое явление, которое можно было бы объяснить этой теорией. Если в своих размышлениях он достигал точки, в которой ему становилось очевидно несоответствие предлагаемой теории и факта реального мира, он сразу же заявлял: “Это не верно, проблема в том-то и том-то”. Он всегда оказывался прав, что озадачивало многих его коллег и буквально лишало их дара речи. Многие современники считали и считают его настоящим гением. Хотели бы стать супергением? Поступайте так же: не дайте математике запугать вас и скрыть от вас физику.
Всегда имейте в виду, что реальный мир находится на первом месте, а математика — на втором. Для успешного решения физической задачи важно не утонуть в математических выкладках и сохранить глобальное видение явления, чтобы удержать контроль над ситуацией. После обучения физике студентов колледжа в течение многих лет я столкнулся с одной из самых крупных проблем в изучении физики: студенты часто напрочь запуганы математикой.
А теперь зададимся одним из наиболее важных вопросов: для чего вам нужна физика? Если вы хотите продолжить свою карьеру в физике или смежной области, то ответ прост: вам нужно знать физику для “ежедневного применения”. Но даже если вы не планируете карьеру физика, вы все еще можете извлечь достаточно много пользы от овладения этим предметом. Многие сведения из вводного курса физики можно применять на практике. Но еще более важным преимуществом овладения физикой является не ее применение на практике, а приобретенные навыки решения задач. Решение физических задач учит вас настойчивости, умению учитывать все варианты решения и выбирать наиболее оптимальный, а также поиску простейшего метода решения.
Измеряем окружающий мир и делаем предсказания
Физики прекрасно умеют измерять и предсказывать явления реального мира. В конце концов, именно потому физика оказалась такой жизнеспособной. Измерение является начальной точкой, на основе которой создается модель явления и делаются предсказания. Множество мер предусмотрено для измерения длины, веса, времени и т.д. Овладение искусством измерения величин является залогом успешного изучения физики.
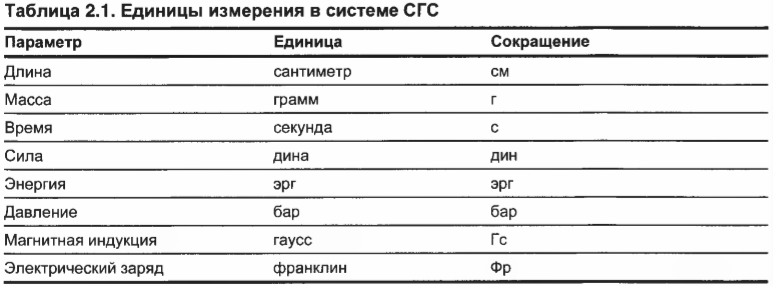
Для достижения согласия в измерениях физики и математики сгруппировали меры в системы единиц измерения. Наиболее распространенными являются система СГС (сантиметр-грамм-секунда) и СИ (система интернациональная). Например, в табл. 2.1 показаны основные единицы измерения в системе СГС. (Пока не стоит напрягаться и запоминать эти единицы, поскольку мы вернемся к ним позже.)
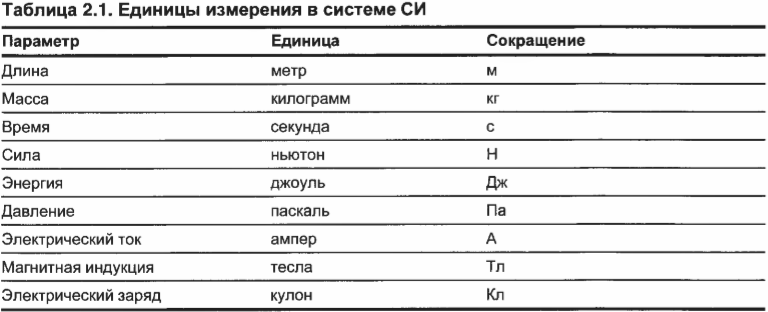
В табл. 2.2 перечислены основные единицы измерения в системе СИ и их сокращения.
Никогда не смешивайте единицы из разных систем
Поскольку в разных системах используются разные единицы длины, то в зависимости от используемой системы можно получать разные численные значения. Например, для измерения глубины плавательного бассейна можно использовать систему СИ, с помощью которой ответ будет выражен в метрах; в системе СГС она будет представлена в сантиметрах, а в еще менее популярной системе — в дюймах.
Предположим, однако, что вам нужно узнать давление воды на дне бассейна. Измеряем глубину бассейна и подставляем найденное значение в формулу давления (см. главы 14 и 15). Однако в этом месте нужно обратить пристальное внимание на используемую систему единиц измерения.
Всегда помните, что в процессе решения задачи нужно использовать одну и ту же систему единиц измерения. Если вы начали решать задачу с помощью системы СИ, то придерживайтесь ее до конца. Иначе вместо правильного ответа вы получите бессмысленную смесь разных величин, поскольку в таком случае вы фактически приравниваете величины, измеренные с помощью разных мерок. Эта ситуация подобна ошибке кулинара, когда, читая рецепт, вместо двух ложек муки он использует два стакана.
В течение многих лет мне приходилось видеть, как студенты ошибочно смешивали величины, полученные с помощью разных систем измерения, и не могли понять причину неправильного решения. Конечно, их намерения были совершенно благородны, идеи прекрасны, выводы уравнений безупречны, а численные значения в ответах получались неверными. Например, в ответе для величины ускорения приведено значение 15, а студент получил 1500. Оказывается, в ответе используется система СИ и ответ дан в метрах на секунду в квадрате, а студент решал задачу с помощью системы СГС и получил правильный ответ, но выраженный в сантиметрах на секунду в квадрате. Численный ответ получился другим именно из-за использования другой системы единиц измерения.
От метров к дюймам и обратно: преобразуем значения из разных единиц измерения
Физики используют разные системы измерения для записи измеренных значений. Но как преобразовать эти значения при переходе от одной системы к другой? При решении физических задач часто приходится иметь дело с величинами, выраженными в разных системах: одни величины могут быть измерены в метрах, другие — в сантиметрах, а третьи — даже в дюймах. Не пугайтесь. Нужно просто научиться их преобразовывать из одной системы в другую. Как проще всего это сделать? Используйте коэффициенты преобразования! Рассмотрим следующую задачу.
Допустим, что за 3 дня вы преодолели расстояние 4680 миль. Впечатляет. Подсчитаем среднюю скорость движения. Как показано в главе 3, в физике скорость определяется так же, как и в жизни: нужно пройденное расстояние поделить на время. Итак, с помощью приведенной ниже формулы получим конечный результат:
Полученный ответ выражен в нестандартных единицах измерения. Обычно для скорости используют другие единицы, например мили в час (в США), а потому нам придется преобразовать полученный ответ в более понятные единицы.
Для преобразования величин из одной системы единиц измерения в другую нужно использовать коэффициенты преобразования. Коэффициент преобразования — это значение, после умножения на которое все нежелательные единицы измерения устраняются, а остаются только нужные.
В предыдущем примере результат получен в милях в день и записан как миль/день. Для вычисления количества миль в час нужно использовать коэффициент преобразования, который позволит исключить дни и оставить часы, т.е. нужно умножить на величину “количество дней в час” (дней/час) и таким образом избавиться от дней:
Коэффициентом преобразования в данном случае является количество дней в час. После подстановки всех значений, упрощения полученного выражения и умножения на коэффициент преобразования получим следующее выражение:
Слова “секунда” (или “метр”) можно рассматривать как некие переменные \( x \)или \( y \), которые исключают друг друга из соотношения, если встречаются одновременно в числителе и знаменателе.
Если числа затуманивают голову, взгляните на единицы измерения
Хотите узнать об одной хитрости, которую применяют учителя при решении задач по физике? Внимательно следите за единицами измерения! Мне приходилось тысячи раз решать задачи “лицом к лицу” со студентами, и я убедился в том, что преподаватели всегда пользуются этим трюком.
Допустим, что нужно определить скорость по заданному расстоянию и времени. Эта задача решается практически мгновенно, потому что всем известно, что расстояние (например, выраженное в метрах), деленное на время (например, выраженное в секундах), дает скорость (выраженную в метрах в секунду).
Однако в более сложных задачах может быть гораздо больше величин, например масса, расстояние, время и т.д. В таких случаях приходится вылавливать в формулировке задачи численные значения и единицы измерения. Как определить количество энергии? Как показано в главе 10, единица энергии выражается как единица массы, умноженная на квадрат единицы длины и деленная на квадрат единицы времени. Если вы сможете легко выделить величины и их единицы измерения, то сможете не запутаться и представить их в решении.
На самом деле единицы измерения — это наши друзья. Они упрощают нам жизнь, в общем, и путь к решению, в частности. Потому если вы чувствуете, что “погрязли» в числах, то проверьте используемые единицы измерения.
Обратите внимание, что в сутках 24 часа, т.е. коэффициент преобразования равен 1/24. Потому преобразование единиц измерения (дней на часы) происходит при умножении величины 1560 миль/день на этот коэффициент преобразования.
При исключении дней во время умножения отношений получается следующий ответ:
Итак, средняя скорость равна 65 милям в час, что достаточно быстро, если ехать с такой средней скоростью на протяжении 3 суток!
Совсем не обязательно использовать коэффициент преобразования. Если инстинктивно вам понятно, что для преобразования единицы измерения “миль в день” в единицу “миль в час” нужно поделить числовое значение на 24, то нечего такой огород городить. Но если вы все же пребываете в сомнениях, то лучше все-таки найти и использовать все нужные коэффициенты преобразования. Лучше пройти этот длинный путь преобразования единиц измерения, чем поспешить и людей насмешить. Мне довольно часто встречались студенты, которые умели успешно решать задачи, но не справлялись с такими преобразованиями.
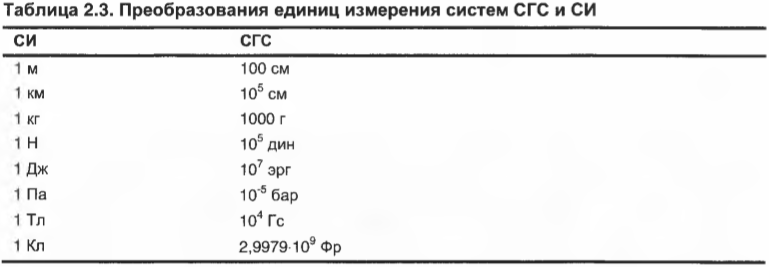
Преобразование суток в часы выполняется легко и просто, поскольку всем известно, что в сутках содержится 24 часа. Однако не все преобразования единиц измерения столь очевидны. Далеко не всем хорошо известны системы единиц СГС и СИ. Потому всегда полезно иметь под рукой табличку преобразований единиц из одной системы в другую, как, например, табл. 2.3. (Расшифровка приведенных здесь сокращений приводится в табл. 2.1 и 2.2.)
Поскольку разница между величинами в двух этих системах практически всегда кратна степеням 10, то преобразование величин выполняется достаточно просто. Например, если шар падает с высоты 5 метров, но вам нужно выразить расстояние в сантиметрах, то для этого достаточно умножить результат на отношение 100 сантиметров/1 метр:
А как преобразовать величины в единицы измерения Английской системы мер на основе фута-фунта-дюйма (foot-pound-inch — FPI)? Нет проблем. Все необходимые сведения о таких преобразованиях приведены в шпаргалке. Держите ее под рукой при чтении этой книги или при решении задач.
Исключаем нули: представляем числа в экспоненциальном виде
Физики часто мысленно погружаются в самые темные глубины и отправляются в самые далекие дали, а потому вынуждены использовать чудовищно большие или малые величины. Например, расстояние от Солнца до Плутона приблизительно равно 5 890 000 000 000 метрам. Что делать с таким огромным количеством метров и нулей? Физики для более удобной работы с такими очень большими или очень малыми величинами используют экспоненциальное представление чисел. В этом представлении нули выражаются в степенях 10. Чтобы определить степень, нужно подсчитать все цифры справа налево до первой цифры (первая цифра будет находиться перед запятой в итоговом экспоненциальном представлении). Итак, расстояние от Солнца до Плутона можно выразить следующим образом:
Экспоненциальное представление чисел также используется для записи очень маленьких значений, где степень имеет отрицательный знак. В таком случае нужно подсчитать количество цифр слева направо от десятичной запятой до места после первой ненулевой цифры (опять первая ненулевая цифра будет находиться перед запятой в итоговом экспоненциальном представлении):
Если число больше 10, то в экспоненциальном представлении оно будет иметь положительную степень, а если меньше 1, то — отрицательную. Как видите, операции с очень большими или малыми числами в экспоненциальном представлении выполняются гораздо проще. Именно поэтому во многих калькуляторах встроена возможность такого представления чисел.
Проверяем точность измерений
Точность имеет огромную важность для измерения и анализа физических параметров. Нельзя считать, что измерение стало более точным, если к измеренной величине необоснованно добавить дополнительное количество значащих цифр. Кроме того, всегда следует указывать оценку ошибки измерения с помощью знака ±. В следующих разделах более подробно описываются указания точности измерения физических величин.
Определяем значащие цифры
В измеренной величине значащими цифрами считаются те, которые были фактически получены в ходе измерения. Так, например, если после измерения ученые сообщили, что ракета прошла расстояние 10,0 за 7,00 секунд, то в результате этих измерений получено по три значащие цифры.
Чтобы определить скорость ракеты, эти данные можно ввести в калькулятор и после деления 10,0 на 7,00 получить, казалось бы, очень точный результат: 1,428571429. Но это совсем не так: если после измерения расстояния и времени для них получено всего по три значащие цифры, то в результате манипуляций с числами точность измерений не может возрасти до десяти значащих цифр. Ведь после измерения расстояния с помощью линейки с миллиметровыми делениями нельзя утверждать, что результат получен с точностью до нескольких микрон.
В примере с ракетой получено только по три значащие цифры, потому величина скорости равна 1,43, а не 1,428571429. Если записать больше цифр, то в таком случае будет сделано ничем необоснованное заявление о повышенной точности измерений, которой не было на самом деле.
При округлении числа нужно учитывать следующее простое правило. Если цифра справа от округляемой цифры больше или равна 5, то округление выполняется в сторону увеличения, а если эта цифра меньше 5, то округление выполняется в сторону уменьшения. Например, число 1,428 округляется до 1,43, а число 1,42 — до 1,4.
А что если в результате двух измерений ракета преодолела 10,0 метров за 7,0 секунд? Одно число имеет три, а другое — две значащих цифры. В таком случае нужно учитывать перечисленные ниже правила округления чисел с разным количеством значащих цифр.
- При умножении или делении чисел результат будет иметь то же количество значащих цифр, что и исходное число с наименьшим количеством значащих цифр.
В примере с ракетой, где нужно поделить расстояние на время, результат будет иметь только две значащие цифры, т.е. правильный ответ равен 1,4 м/с.
- При сложении или вычитании чисел нужно расположить их в столбик и выровнять по положению десятичной запятой в числах; самая последняя значащая цифра в результате будет соответствовать самой правой значащей цифре в том столбце, в котором все числа в столбике имеют значащие цифры.
Например, при сложении чисел 3,6, 14 и 6,33 получим:
Здесь нужно округлить результат до целого числа, поскольку число 14 не имеет значащих цифр после десятичной запятой, т.е. до 24.
По соглашению нули, используемые доя заполнения пустых мест до или после десятичной запятой, не считаются значащими цифрами. Например, по умолчанию число 3600 имеет только две значащие цифры. Но если некая величина измерена с высокой точностью и действительно равна 3600, то для подчеркивания точности измерения ее иногда приводят с указанием знака, отделяющего целую часть числа от десятичной дроби 3600,0.
Оцениваем точность
Физики при записи результатов измерений не всегда полагаются только на значащие цифры, и иногда можно встретить следующую запись:
Символ ± обозначает оценку физика возможной ошибки измерения. Физик сообщает таким образом, что действительное значение измеряемой величины находится в промежутке от 5,36+0,05 (т.е. 5,41) до 5,36-0,05 (т.е. 5,31) метров. (Это не значит, что именно настолько измеренное значение отличается от “истинного”. Это просто оценка точности измерения, т.е. насколько надежно это измерение.)
Определяем размер ±
С недавних пор символ ± стал чрезвычайно популярным, и его можно встретить даже в объявлениях о продаже недвижимости, например “продается 35± акров”. Иногда даже публикуются объявления о продаже ±35 акров. Значит ли это, что в итоге вы можете приобрести участок площадью в диапазоне от «-35 до +35 акров? Что значит приобрести -15 акров? Может быть, то, что после приобретения такого участка вы будете должны 15 акров?
Вспоминаем алгебру
В физике используется довольно много уравнений, и чтобы умело работать с ними, нужно овладеть основными приемами манипулирования частями уравнения. Сейчас самое время напомнить некоторые основные сведения из курса алгебры.
Следующее уравнение выражает расстояние \( s \), которое проходит объект с ускорением \( a \) за время \( t \):
Допустим, что нужно определить ускорение по известному времени движения и пройденному расстоянию. Манипулируя отдельными членами уравнения, получим следующее соотношение:
Для получения такого соотношения для \( a \) нужно обе стороны предыдущего выражения умножить на 2 и поделить на \( t^2 \).
А что если нужно найти время \( t \)? С помощью несложных манипуляций с переменными и числами получим следующее соотношение:
Нужно ли запоминать все эти три варианта одного уравнения? Конечно же, нет. Достаточно запомнить только один вариант, который связывает эти три величины (расстояние, ускорение и время), а потом извлекать из него соотношение для нужной переменной. (В шпаргалке приводится несколько основных соотношений, которые следует помнить.)
Немного тригонометрии
Кроме базовых сведений из алгебры для решения физических задач необходимо также иметь некоторые сведения из тригонометрии, например о синусе, косинусе, тангенсе. Для этого нужно запомнить простые соотношения на основе прямоугольного треугольника, который показан на рис. 2.1 во всей своей красе.
Для определения тригонометрических величин с помощью треугольника на рис. 2.1 нужно поделить длину одной стороны на длину другой, как показано ниже:
Эти простые соотношения пригодятся нам при изучении векторов в главе 4 и при решении многих задач по физике.
Зная величину одного острого угла и длину одной стороны этого треугольника, можно найти величину другого угла и длины двух других сторон. Ниже приводится несколько примеров, которые по мере изучения курса станут для вас просто родными, но которые вовсе не нужно запоминать наизусть. Если вы знаете предшествующие соотношения для синуса, косинуса и тангенса, то вы сможете легко вывести приведенные ниже соотношения:
Помните, что можно пойти и в “обратную сторону”, т.е. вычислить обратные функции для синуса (\( sin^{-1} \), или \( arcsin \)), косинуса (\( cos^{-1} \), или \( arccos \)) или тангенса (\( tan^{-1} \), или \( arctg \)). Вот как они определяются:
(Строго говоря, обратной синусу функцией является функция “арксинус”, или \( arcsin(x) \), обратной косинусу — “арккосинус”, или \( arccos(x) \), обратной тангенсу — “арктангенс”, или \( arctg(x) \). Обозначения \( sin^{-1}(x) \), \( cos^{-1}(x) \) и \( tg^{-1}(x) \) часто используются в иностранной литературе для обозначения функций “арксинус”, “арккосинус” и “арктангенс”, но их не рекомендуется употреблять, чтобы не путать с функциями \( 1/sin(x) \), \( 1/cos(x) \) и \( 1/tg(x) \). — Примеч. ред.)






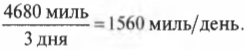
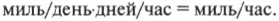
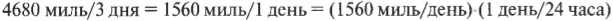

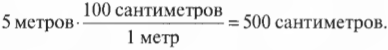
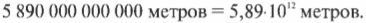


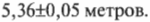
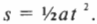
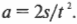
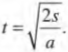

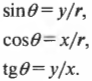
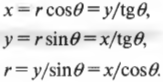
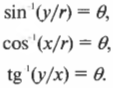
Добавить комментарий
Стивен Хольцнер Физика для чайников
хочу сказать огромное спасиюо за данный учебник так как я недавно в 5 класс перешол меня сильно вдохновила физика я просто всю ночь сижу чтоб это почитать
Привет спасибо, за интересный материал физика это прикольно Я учусь 5 классе и хочу изучать физику.
muy muy interesante
Спасибо за интересный материал. А где шпаргалка, которую периодически упоминают в тексте?
на этом обучение стоит прекратить, потому как дальше будет все еще сложнее
А почему при пересчете скорости вы пишите «При исключении дней во время умножения отношений получается следующий ответ:» разве тут не деление? формула, впрочем, тоже в итоге дает деление.
Спасибо
Все просто и понятно.Спасибо!