Законы сохранения в механике

Содержание
Импульс тела
Импульс тела – это векторная физическая величина, равная произведению массы тела на его скорость:
Обозначение – \( p \), единицы измерения – (кг·м)/с.
Импульс тела – это количественная мера движения тела.
Направление импульса тела всегда совпадает с направлением скорости его движения.
Изменение импульса тела равно разности конечного и начального значений импульса тела:
где \( p_0 \) – начальный импульс тела,
\( p \) – конечный импульс тела.
Если на тело действует нескомпенсированная сила, то его импульс изменяется. При этом изменение импульса тела равно импульсу подействовавшей на него силы.
Импульс силы – это количественная мера изменения импульса тела, на которое подействовала эта сила.
Обозначение – \( F\!\Delta t \), единицы измерения — Н·с.
Импульс силы равен изменению импульса тела:
Направление импульса силы совпадает по направлению с изменением импульса тела.
Второй закон Ньютона (силовая форма):
Важно!
Следует всегда помнить, что совпадают направления векторов:
• силы и ускорения: \( \vec{F}\uparrow\uparrow\vec{a} \);
• импульса тела и скорости: \( \vec{p}\uparrow\uparrow\vec{v} \);
• изменения импульса тела и силы: \( \Delta\vec{p}\uparrow\uparrow\vec{F} \);
• изменения импульса тела и ускорения: \( \Delta\vec{p}\uparrow\uparrow\vec{a} \).
Импульс системы тел
Импульс системы тел равен векторной сумме импульсов тел, составляющих эту систему:
При рассмотрении любой механической задачи мы интересуемся движением определенного числа тел. Совокупность тел, движение которых мы изучаем, называется механической системой или просто системой.
Рассмотрим систему, состоящую из трех тел. На тела системы действуют внешние силы, а между телами действуют внутренние силы.
\( F_1,F_2,F_3 \) – внешние силы, действующие на тела;
\( F_{12}, F_{23}, F_{31}, F_{13}, F_{21}, F_{32} \) – внутренние силы, действующие между телами.
Вследствие действия сил на тела системы их импульсы изменяются. Если за малый промежуток времени сила заметно не меняется, то для каждого тела системы можно записать изменение импульса в виде уравнения:
В левой части каждого уравнения стоит изменение импульса тела за малое время \( \Delta t \).
Обозначим: \( v_0 \) – начальные скорости тел, а \( v^{\prime} \) – конечные скорости тел.
Сложим левые и правые части уравнений.
Но силы взаимодействия любой пары тел в сумме дают нуль.
Важно!
Импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.
Закон сохранения импульса
Закон сохранения импульса
Векторная сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой:
Замкнутая система – это система, на которую не действуют внешние силы.
Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций.
При абсолютно упругом ударе взаимодействующие тела до и после взаимодействия движутся отдельно.
Закон сохранения импульса для абсолютно упругого удара:
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.
Закон сохранения импульса для абсолютно неупругого удара:
Реактивное движение – это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-то его части.
Принцип реактивного движения основан на том, что истекающие из реактивного двигателя газы получают импульс. Такой же по модулю импульс приобретает ракета.
Для осуществления реактивного движения не требуется взаимодействия тела с окружающей средой, поэтому реактивное движение позволяет телу двигаться в безвоздушном пространстве.
Реактивные двигатели
Широкое применение реактивные двигатели в настоящее время получили в связи с освоением космического пространства. Используются они также для метеорологических и военных ракет различного радиуса действия. Кроме того, все современные скоростные самолеты оснащены воздушно-ракетными двигателями.
Реактивные двигатели делятся на два класса:
- ракетные;
- воздушно-реактивные.
В ракетных двигателях топливо и необходимый для его горения окислитель находятся непосредственно внутри двигателя или в его топливных баках.
Ракетный двигатель на твердом топливе
При горении топлива образуются газы, имеющие очень высокую температуру и оказывающие давление на стенки камеры. Сила давления на переднюю стенку камеры больше, чем на заднюю, где находится сопло. Выходящие через сопло газы не встречают на своем пути стенку, на которую могли бы оказать давление. В результате появляется сила, толкающая ракету вперед.
Сопло – суженная часть камеры, служит для увеличения скорости истечения продуктов сгорания, что, в свою очередь, повышает реактивную силу. Сужение струи газа вызывает увеличение его скорости, так как при этом через меньшее поперечное сечение в единицу времени должна пройти такая же масса газа, что и при большем поперечном сечении.
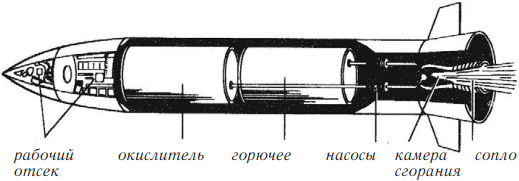
Ракетный двигатель на жидком топливе
В ракетных двигателях на жидком топливе в качестве горючего используют керосин, бензин, спирт, жидкий водород и др., а в качестве окислителя – азотную кислоту, жидкий кислород, перекись водорода и пр.
Горючее и окислитель хранятся отдельно в специальных баках и с помощью насосов подаются в камеру сгорания, где температура достигает 3000 0С и давление до 50 атм. В остальном работает так же, как и двигатель на твердом топливе.
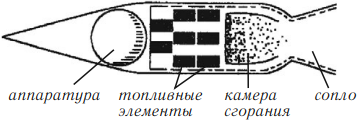
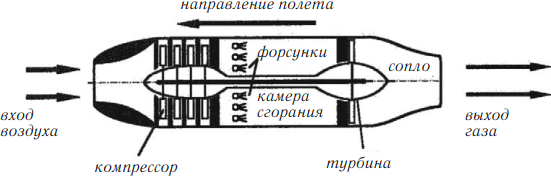
Воздушно-реактивный двигатель
В носовой части находится компрессор, засасывающий и сжижающий воздух, который затем поступает в камеру сгорания. Жидкое горючее (керосин) попадает в камеру сгорания с помощью специальных форсунок. Раскаленные газы выходят через сопло, вращают газовую турбину, приводящую в движение компрессор.
Основное отличие воздушно-реактивных двигателей от ракетных двигателей состоит в том, что окислителем для горения топлива служит кислород воздуха, поступающего внутрь двигателя из атмосферы.
Алгоритм применения закона сохранения импульса к решению задач:
- Запишите краткое условие задачи.
- Определите характер движения и взаимодействия тел.
- Сделайте рисунок, на котором укажите направление векторов скоростей тел до и после взаимодействия.
- Выберите инерциальную систему отсчета с удобным для нахождения проекций векторов направлением координатных осей.
- Запишите закон сохранения импульса в векторной форме.
- Спроецируйте его на выбранные координатные оси (сколько осей, столько и уравнений в системе).
- Решите полученную систему уравнений относительно неизвестных величин.
- Выполните действия единицами измерения величин.
- Запишите ответ.
Работа силы
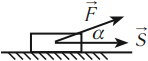
Механическая работа – это скалярная векторная величина, равная произведению модулей вектора силы, действующей на тело, вектора перемещения и косинуса угла между этими векторами.
Обозначение – \( A \), единицы измерения – Дж (Джоуль).
1 Дж – это работа, которую совершает сила в 1 Н на пути в 1 м:
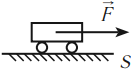
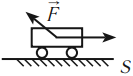
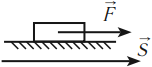
Механическая работа совершается, если под действием некоторой силы, направленной не перпендикулярно, тело перемещается на некоторое расстояние.
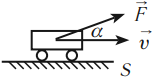
Зависимость механической работы от угла \( \alpha \)
- \( \alpha=0^{\circ},\, \cos\alpha=1,\, A=FS,\,A>0; \)
- \( 0^{\circ}<\alpha<90^{\circ},\, A=FS\cos\alpha,\,A>0; \)
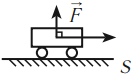
- \( \alpha=90^{\circ},\, \cos\alpha=0,\, A=0; \)
- \( 90^{\circ}<\alpha<180^{\circ},\, A=FS\cos\alpha,\,A<0; \)
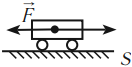
\( \alpha=180^{\circ},\, \cos\alpha=-1,\, A=-FS,\,A<0; \)
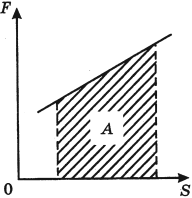
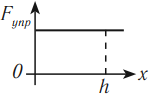
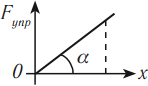
Геометрический смысл механической работы
На графике зависимости \( F=F(S) \) работа силы численно равна площади фигуры, ограниченной графиком, осью перемещения и прямыми, параллельными оси силы.
Формулы для вычисления работы различных сил
Работа силы тяжести:
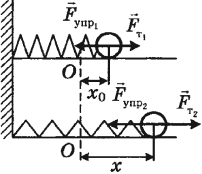
Работа силы упругости:
Коэффициент полезного действия механизма (КПД) — это физическая величина, равная отношению полезной работы, совершенной механизмом, ко всей затраченной при этом работе.
Обозначение – \( \eta \), единицы измерения – %.
\( A_{\mathit{пол.}} \) – полезная работа – это та работа, которую нужно сделать;
\( A_{\mathit{зат.}} \) – затраченная работа – это та работа, что приходится делать на самом деле.
Важно!
КПД любого механизма не может быть больше 100%.
Мощность
Мощность – это количественная мера быстроты совершения работы.
Обозначение – \( N \), единицы измерения – Вт (Ватт).
Мощность равна отношению работы к времени, за которое она была совершена: .
1 Вт – это мощность, при которой за 1 с совершается работа в 1 Дж:
1 л. с. (лошадиная сила) = 735 Вт.
Связь между мощностью и скоростью равномерного движения:
Таким образом, мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов.
Важно!
Если интервал времени стремится к нулю, то выражение представляет собой мгновенную мощность, определяемую через мгновенную скорость.
Работа как мера изменения энергии
Если система тел может совершать работу, то она обладает энергией.
Работа и изменение кинетической энергии (теорема о кинетической энергии)
Если под действием силы тело совершило перемещение и вследствие этого его скорость изменилась, то работа силы равна изменению кинетической энергии.
Силы, работа которых не зависит от формы траектории, называются консервативными.
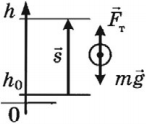
Работа и изменение потенциальной энергии тела, поднятого над землей
Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.
Работа и изменение потенциальной энергии упруго деформированного тела
Работа силы упругости равна изменению потенциальной энергии, взятому с противоположным знаком.
Кинетическая энергия
Кинетическая энергия – это энергия, которой обладает тело вследствие своего движения.
Обозначение – \( W_k (E_k) \), единицы измерения – Дж.
Кинетическая энергия равна половине произведения массы тела на квадрат его скорости:
Важно!
Так как кинетическая энергия отдельного тела определяется его массой и скоростью, то она не зависит от того, взаимодействует ли это тело с другими телами или нет. Значение кинетической энергии зависит от выбора системы отсчета, как и значение скорости. Кинетическая энергия системы тел равна сумме кинетических энергий отдельных тел, входящих в эту систему.
Потенциальная энергия
Потенциальная энергия – это энергия взаимодействия тел или частей одного и того же тела.
Обозначение – \( W_p (E_p) \), единицы измерения – Дж.
Потенциальная энергия тела, поднятого на некоторую высоту над землей, равна произведению массы тела, ускорения свободного падения и высоты, на которой он находится:
Потенциальная энергия упруго деформированного тела равна половине произведения жесткости на квадрат удлинения:
Важно!
Величина потенциальной энергии зависит от выбора нулевого уровня. Нулевым называется уровень, на котором потенциальная энергия равна нулю. Нулевой уровень выбирается произвольно, исходя из удобства решения задачи.
Закон сохранения механической энергии
Полная механическая энергия – это энергия, равная сумме кинетической и потенциальной энергий.
Обозначение – \( W (E) \), единицы измерения – Дж.
Закон сохранения механической энергии
В замкнутой системе тел, между которыми действуют только консервативные силы, механическая энергия сохраняется, т. е. не изменяется с течением времени:
Если между телами системы действуют кроме сил тяготения и упругости другие силы, например сила трения или сопротивления, действие которых приводит к превращению механической энергии в тепловую, то в такой системе тел закон сохранения механической энергии не выполняется.
Важно!
В случае, если кроме консервативных сил (тяжести, упругости, тяготения) существуют еще и неконсервативные силы, например сила трения, а также внешние силы, то
Теорема о кинетической энергии справедлива для сил любой природы:
Если на систему тел действуют неконсервативные и внешние силы, то изменение полной энергии равно сумме работ неконсервативных и внешних сил.
Закон сохранения и превращения энергии
Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой или передается от одного тела к другому.






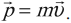
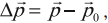
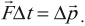
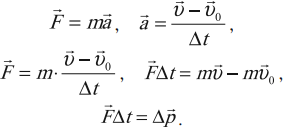
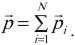
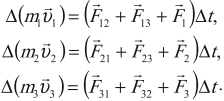
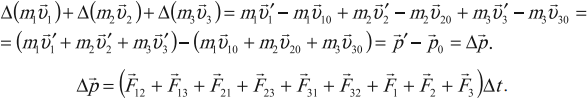
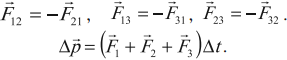
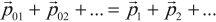
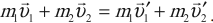
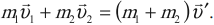
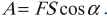
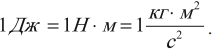
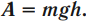
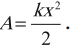
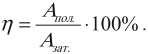
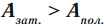
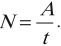
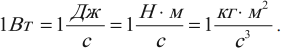
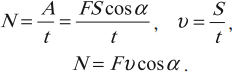
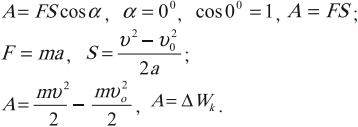
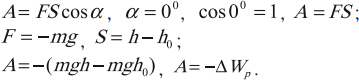
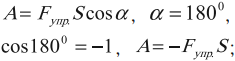
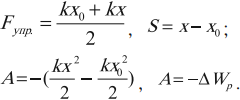
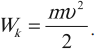
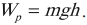
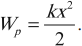
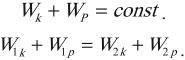

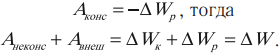


Добавить комментарий