Молекулярная физика

Молекулярная физика – раздел физики, в котором свойства вещества изучаются на основе его молекулярного (микроскопического) строения.
Молекулярно-кинетической теорией (МКТ) называется теория, объясняющая строение и свойства тел движением и взаимодействием частиц, из которых состоят тела.
В основе МКТ лежат следующие основные положения:
- все тела состоят из частиц, разделенных промежутками;
- частицы вещества находятся в непрерывном хаотическом движении;
- частицы взаимодействуют между собой.
Атомом называется мельчайшая частица химического элемента. Атом электрически нейтрален. Размеры атома порядка 10-10 м. Атомы одного и того же химического элемента одинаковы. Атом состоит из положительно заряженного ядра и отрицательно заряженных электронов. В состав атомного ядра входят протоны и нейтроны. Атомы соединяются в молекулы.
Молекула – наименьшая устойчивая частица данного вещества, обладающая его химическими свойствами. Размеры молекул 10-10–10-7 м. Молекулы одного вещества одинаковы. Молекулы электрически нейтральны.
Макроскопическое тело – тело, состоящее из очень большого числа частиц.
Макроскопические параметры – величины, характеризующие состояние макроскопических тел без учета их молекулярного строения.
Микроскопические параметры – величины, являющиеся характеристиками частицы (молекулы) вещества.
Тепловое (термодинамическое) равновесие – состояние тела или системы тел, при котором его термодинамические параметры (\( p, V, m \) и др.) остаются неизменными сколь угодно долго.
Содержание
- Модели строения газов, жидкостей и твердых тел
- Тепловое движение атомов и молекул вещества
- Броуновское движение
- Диффузия
- Экспериментальные доказательства атомистической теории. Взаимодействие частиц вещества
- Модель идеального газа
- Связь между давлением и средней кинетической энергией теплового движения молекул идеального газа
- Абсолютная температура
- Связь температуры газа со средней кинетической энергией его частиц
- Уравнение p=nkT
- Уравнение Менделеева – Клапейрона
- Изопроцессы: изотермический, изохорный, изобарный, адиабатный процессы
- Насыщенные и ненасыщенные пары
- Влажность воздуха
- Изменение агрегатных состояний вещества: испарение и конденсация, кипение жидкости
- Изменение агрегатных состояний вещества: плавление и кристаллизация
- Изменение энергии в фазовых переходах
- Основные формулы по теме «Молекулярная физика»
Модели строения газов, жидкостей и твердых тел
Все вещества могут существовать в трех агрегатных состояниях – твердом, жидком и газообразном. Четвертым агрегатным состоянием вещества считают плазму. Агрегатное состояние зависит от физических условий, в которых находится вещество. Существование у вещества нескольких агрегатных состояний обусловлено различиями в тепловом движении его молекул (атомов) и в их взаимодействии при разных условиях. Переходы между агрегатными состояниями сопровождаются скачкообразным изменением ряда физических свойств (плотности, теплопроводности и др.). Рассмотрим особенности строения газов, жидкостей и твердых тел.
В газах силы притяжения между молекулами очень малы. Частицы газа находятся на больших расстояниях друг от друга: расстояния между частицами гораздо больше размеров самих частиц. Частицы газа движутся беспорядочно. Кинетическая энергия молекул газа гораздо больше потенциальной энергии их взаимодействия. Порядок в расположении частиц отсутствует. Это объясняет следующие свойства газа: газы занимают весь объем сосуда, не имеют формы, легко сжимаемы.
Молекулы жидкости сильно взаимодействуют друг с другом и расположены очень близко друг к другу. Однако такое расположение частиц не является строго упорядоченным по всему объему. Говорят, что в жидкостях наблюдается ближний порядок – упорядоченное относительное расположение соседних частиц жидкости. Потенциальная энергия взаимодействия молекул жидкости сравнима с их кинетической энергией. Молекулы жидкости совершают хаотические колебания около положений равновесия. Эти колебания происходят внутри свободного объема, предоставляемого молекулам ее соседями. Через некоторое время положение равновесия смещается, и частица жидкости совершает скачок. Свойства жидкостей одинаковы по всем направлениям. Основные свойства жидкостей: жидкости имеют определенный объем, но не сохраняют форму, текучи и мало сжимаемы.
В твердых телах силы взаимного притяжения частиц очень велики. Частицы твердых тел не могут уйти со своих мест на большое расстояние. Потенциальная энергия взаимодействия молекул твердого тела больше их кинетической энергии. Движение частиц представляет собой колебания относительно их положений равновесия – узлов кристаллической решетки.
Твердые тела делятся на кристаллические и аморфные. Кристаллические твердые тела имеют упорядоченное, периодически повторяющееся в пространстве расположение частиц – кристаллическую решетку. Одиночные кристаллы, имеющие форму правильных многогранников, называются монокристаллами. Для таких тел характерна анизотропия – зависимость физических свойств от направления. Большинство твердых тел представляют собой сросшиеся монокристаллы – поликристаллы. Поликристаллы изотропны – их физические свойства одинаковы по всем направлениям. В кристаллических твердых телах имеется дальний порядок в расположении частиц: упорядоченное расположение частиц повторяется по всему объему кристалла. В аморфных телах атомы колеблются около хаотически расположенных точек. Свойства аморфных тел: они изотропны, не имеют постоянной температуры плавления, обладают текучестью. Примерами аморфных тел являются смола, янтарь, стекло. Свойства твердых тел: они сохраняют форму и объем, мало сжимаемы, имеют определенную температуру плавления.
Тепловое движение атомов и молекул вещества
Молекулы (атомы) вещества всегда находятся в постоянном беспорядочном движении независимо от того, имеем ли мы дело с твердым, жидким или газообразным состоянием вещества. Это движение обусловливает собой наличие в любом веществе внутренней кинетической энергии, связанной с температурой вещества.
Тепловое движение – это беспорядочное хаотическое движение частиц, из которых состоит вещество.
Тепловым движением объясняется, например, давление газа на стенки сосуда, теплопроводность, т. е. перенос тепла от более нагретого к менее нагретому телу.
Хаотичность является важнейшей чертой теплового движения. Нельзя точно определить координаты молекулы и ее скорость (импульс), поэтому используют усредненные или вероятностные значения координат и импульса. При механическом движении координаты и импульс объекта определяются строго из законов динамики Ньютона и кинематических уравнений.
Температура тела зависит от средней кинетической энергии молекул. Скорость теплового движения частиц увеличивается с ростом температуры. Эксперименты показывают, что при любой температуре в веществе есть молекулы, двигающиеся довольно медленно, и молекулы, скорость которых высока. Если количество молекул вещества, имеющих высокую скорость, увеличивается, т. е. увеличивается средняя скорость молекул, то это значит, что температура вещества также увеличивается.
Важно!
В тепловом движении молекул и атомов участвуют абсолютно все молекулы тела, именно поэтому с изменением теплового движения меняется и состояние самого тела, его различные свойства.
Броуновское движение
Броуновским движением называют тепловое движение взвешенных в жидкости или газе частиц. Это движение в 1827 г. впервые наблюдал английский ботаник Р. Броун, рассматривая в микроскоп взвешенные в воде споры плауна. Интенсивность броуновского движения не зависит от времени, но возрастает с ростом температуры среды, с уменьшением вязкости и размеров частиц.
Причиной броуновского движения частицы являются беспорядочные нескомпенсированные удары молекул жидкости (газа) о взвешенную частицу. Молекулы среды движутся хаотически, и взвешенная частица в любой момент времени подвергается неуравновешенным воздействиям, сила которых непрерывно изменяется по величине и направлению. Если бы частица была большой, то молекулы равномерно толкали бы ее со всех сторон, и она оставалась бы на месте. Но небольшая частица имеет маленькую поверхность, и удары молекул не уравновешивают друг друга. Равнодействующая сил не равна нулю, и в течение времени меняется по величине и направлению. Так как молекулы среды движутся беспорядочно, число ударов о броуновскую частицу быстро изменяется, и скорость ее меняется по величине и направлению. В результате частица перемещается по сложной траектории.
Теория броуновского движения была создана в 1905 г. А. Эйнштейном и М. Смолуховским. Эйнштейн доказал, что при движении броуновской частицы средний квадрат смещения молекулы пропорционален времени ее движения.
В 1908 г. Ж. Перрен изучал движение нерастворимых в жидкости частиц в горизонтальной кювете в воде и их распределение в поле силы тяжести в узкой вертикальной кювете. Выявленные закономерности полностью подтвердили теорию Эйнштейна. На основе экспериментов Перрена удалось найти с достаточной точностью число Авогадро.
Броуновское движение в метрологии является основной причиной, по которой точность чувствительных измерительных приборов ограничена, потому что тепловое движение атомов деталей приборов и окружающей среды вызывает дрожание стрелок измерительных приборов.
Диффузия
Диффузия – явление взаимного проникновения молекул соприкасающихся веществ в межмолекулярные промежутки друг друга. Так как молекулы вещества хаотически движутся, то они проникают в межмолекулярные промежутки соприкасающегося с ним тела и распределяются между ними. Диффузия приводит к выравниванию концентраций соприкасающихся веществ.
Это явление наблюдается в газах, жидкостях и твердых телах. Скорость диффузии наибольшая в газах, а самая маленькая в твердых телах. Скорость диффузии увеличивается при повышении температуры. Диффузия играет существенную роль в природе.
Диффузия газов обеспечивает однородность атмосферы вблизи поверхности Земли. Диффузия способствует нормальному питанию растений, животных.
Экспериментальные доказательства атомистической теории. Взаимодействие частиц вещества
Атомистическая гипотеза была выдвинута Демокритом около 2500 лет назад. Такие ученые как Декарт, Ломоносов, Ньютон считали, что материя состоит из мельчайших неделимых частиц. Однако в их работах не было приведено доказательства их существования. Количественное обоснование теории было дано в работах Дальтона, Гей-Люссака, Авогадро.
МКТ подтверждена многочисленными опытами и наблюдениями.
Первое положение МКТ — все тела состоят из частиц (атомов, молекул, ионов и др.), разделенных промежутками.
Его подтверждают явления испарения жидкостей и твердых тел, делимости веществ, диффузии, броуновского движения, растворения веществ, окрашивания воды крупинкой краски, сжимаемости веществ. Экспериментальным подтверждением существования отдельных, разделенных промежутками частиц могут служить проницаемость, сжимаемость, растворимость веществ.
Косвенными доказательствами являются фотографии молекул и групп атомов, полученные с помощью электронного микроскопа, измерения масс и размеров молекул – например, образование пленки олеиновой кислоты на поверхности воды. Полагая, что эта пленка имеет толщину в одну молекулу, получаем диаметр молекулы \( d \).
где \( V \) – объем капли олеиновой кислоты, \( S \) – площадь пленки на поверхности воды.
Существование молекул доказывает закон кратных соотношений (закон Дальтона): при образовании из двух элементов различных веществ массы одного из элементов в разных соединениях находятся в кратных отношениях. Например:
Существование промежутков доказывает тот факт, что при смешивании различных жидкостей объем смеси меньше суммы объемов отдельных жидкостей; диффузия; деформация.
Массы атомов и молекул определяют по формуле:
где \( M \) – молярная масса, \( N_A \) – постоянная Авогадро.
Постоянная Авогадро – число атомов, молекул (структурных элементов) в одном моле любого вещества:
Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде массой 0,012 кг. Моль – основная единица Международной системы (СИ).
Важно!
В одном моле любого вещества содержится одинаковое число частиц – 6·1023 частиц.
Так как массы молекул очень малы, удобно использовать в расчетах не абсолютные значения масс, а относительные. По международному соглашению массы всех атомов и молекул сравнивают с \( \frac{1}{12} \) массы атома углерода (углеродная шкала атомных масс).
Относительной молекулярной (или атомной) массой вещества \( M_r \) называют отношение массы молекулы (или атома) \( m_0 \) данного вещества к \( \frac{1}{12} \) массы атома углерода \( m_{0C} \):
Относительные атомные массы всех химических элементов точно определены. Складывая относительные атомные массы, можно вычислить относительную молекулярную массу.
Чем больше атомов и молекул содержится в макроскопическом теле, тем больше вещества содержится в нем. Число молекул в макроскопических телах огромно, поэтому удобно указывать не абсолютное число атомов или молекул, а относительное. Принято сравнивать число молекул или атомов в данном теле с числом атомов, содержащихся в углероде массой 12 г.
Относительное число атомов или молекул в теле характеризует особая физическая величина: количество вещества.
Обозначение – \( \nu \), единица измерения в СИ – моль.
Количеством вещества \( \nu \) называют отношение числа молекул \( N \) в данном теле к числу атомов в 0,012 кг углерода:
Молярной массой вещества \( M \) называют массу вещества, взятого в количестве 1 моля:
Важно!
В СИ единица измерения молярной массы – кг/моль.
Второе положение МКТ — движение частиц.
Это положение доказывают диффузия, броуновское движение, существование давления газа на стенки сосуда.
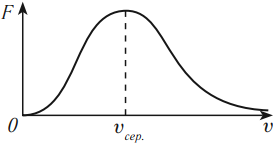
В 1860 году Максвелл пришел к выводу о том, что молекулы газа движутся с различными скоростями. Он вывел закон распределения молекул газа по скоростям. Значительное число молекул движется со скоростью, названной наиболее вероятной. Она зависит от температуры – чем выше температура, тем больше эта скорость. Число молекул, движущихся со скоростями больше или меньше наиболее вероятной скорости, мало. Эта скорость по теоретическим расчетам составляет несколько сотен метров в секунду при нуле градусов Цельсия.
На графике по оси абсцисс отложены значения модуля скорости частиц, по оси ординат – относительное число молекул, скорости которых лежат в интервале от \( v \) до \( v+\Delta v \) (это отношение обозначено \( F \)).
Экспериментально скорость движения молекул была определена в опыте Штерна в 1920 году.
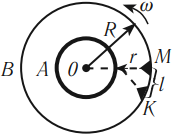
Экспериментальная установка представляла собой два цилиндра разных радиусов, обладающих общей осью вращения, которые приводились во вращение с большой скоростью. На оси внутреннего цилиндра располагалась платиновая проволока, покрытая серебром. При пропускании по ней тока проволока нагревалась, и атомы серебра испарялись с нее. На внутреннем цилиндре была сделана прорезь. Установка помещалась в вакуум.
Если цилиндры были неподвижны, то атомы серебра осаждались на внешнем цилиндре напротив щели. При вращении цилиндров полоска смещалась относительно прорези и была неоднородна по толщине. Это доказывало, что скорость атомов серебра разная и что число частиц, движущихся с различными скоростями, неодинаково. Толщина слоя определяется числом частиц, движущихся с определенной скоростью.
Третье положение МКТ — частицы вещества взаимодействуют друг с другом силами притяжения и отталкивания.
Эти силы зависят от расстояния: с увеличением расстояния преобладают силы притяжения, при уменьшении – силы отталкивания. Взаимодействие частиц доказывает деформация, существование различных агрегатных состояний вещества, сохранение формы и объема твердого тела, смачивание и капиллярность (существование сил поверхностного натяжения жидкости), опыт с двумя свинцовыми цилиндрами, которые, будучи притерты друг к другу свежими срезами, выдерживают значительную нагрузку.
Силы межмолекулярного взаимодействия имеют электромагнитную природу, хотя в целом молекула электрически нейтральна (суммы положительных и отрицательных зарядов составляющих ее частиц равны). Электрическое поле молекулы на расстоянии, большем 2–3 ее диаметров, можно считать равным нулю. Принято считать силы притяжения отрицательными, а силы отталкивания положительными. При сближении молекул возникает взаимодействие электрических зарядов ядер и электронных оболочек молекул: разноименные заряды притягиваются, одноименные отталкиваются; между молекулами возникают силы притяжения. Расстояния между центрами молекул при этом порядка 10-9 м. Когда молекулы «соприкоснутся» своими электронными оболочками, дальнейшее сближение станет невозможным, и возникнут большие силы отталкивания. Расстояния между центрами молекул при этом порядка 10-10 м.
При растяжении тела увеличиваются расстояния между частицами и возникают силы притяжения, а при сжатии расстояние между частицами становится меньше и начинают действовать силы отталкивания. В обоих случаях возникает сила упругости, стремящаяся вернуть тело в исходное состояние.
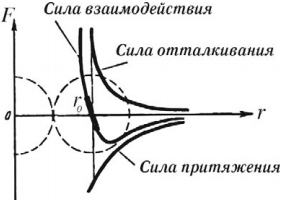
Зависимость силы взаимодействия между молекулами от расстояния показана на рисунке. \( F \) – проекция силы взаимодействия, которая отрицательна в случае притяжения и положительна при отталкивании частиц, \( r \) – расстояние между частицами. При сближении сила взаимодействия сначала растет по модулю, затем убывает (область притяжения частиц). При переходе через \( r = r_0 \) сила взаимодействия изменяет знак и очень быстро увеличивается по модулю при уменьшении расстояния (область отталкивания частиц). Расстояние \( r_0 \) соответствует устойчивому равновесию двух частиц. При отклонении от него в любую сторону возникает сила, возвращающая молекулы в состояние равновесия. Этому расстоянию соответствует минимальная потенциальная энергия.
Модель идеального газа
В молекулярно-кинетической теории используется идеализированная модель – идеальный газ.
Идеальный газ – газ, молекулы которого не взаимодействуют между собой.
Эта модель удовлетворяет следующим условиям:
- молекулы газа можно считать материальными точками, так как расстояния между ними намного больше, чем их размеры;
- молекулы газа представляют собой упругие шарики конечных малых размеров. Соударения молекул идеального газа между собой и стенками сосуда абсолютно упругие;
- движение каждой частицы подчиняется законам динамики.
По своим свойствам близки к идеальному газу разреженные газы (при малом давлении и не слишком низких температурах).
Связь между давлением и средней кинетической энергией теплового движения молекул идеального газа
Большое число молекул газа и хаотичность их движения приводит к тому, что все направления их движения встречаются одинаково часто. Соударения между частицами приводят к непрерывному изменению их скоростей. Поэтому для описания движения одной частицы можно использовать законы Ньютона, а для описания движения большого числа частиц эти законы использовать нельзя. Для описания поведения большого числа частиц используют теорию вероятностей, с помощью которой находят средние значения физических величин – среднее значение скорости частицы \( v \), среднее значение кинетической энергии частицы \( E \).
Основное уравнение МКТ устанавливает связь между макропараметром – давлением и микропараметрами, характеризующими частицу. Давление идеального газа пропорционально произведению массы молекулы на концентрацию молекул и средний квадрат их скорости:
где \( m_0 \) – масса частицы, \( n \) – концентрация частиц, \( \overline{v^2} \) – среднее значение квадрата скорости.
Среднее значение квадрата скорости находится по формуле:
где \( \overline{v_x^2},\,\overline{v_y^2},\,\overline{v_z^2} \) – средние значения квадрата проекции скорости на оси ОХ, ОУ и ОZ соответственно.
Среднее значение квадрата проекции скорости на оси ОХ вычисляется по формуле:
Аналогично вычисляются средние значения квадрата проекции скорости на оси ОУ и ОZ.
Так как все направления движения из-за хаотичности движения молекул равновероятны, то:
Множитель \( \frac{1}{3} \) появляется вследствие существования трех проекций у любого вектора скорости.
Важно!
При решении задач не путать среднее значение квадрата скорости и среднюю квадратичную скорость \( v_{ск}=\sqrt{\overline{v^2}} \) (м/с). Единица измерения в СИ среднего значения квадрата скорости – м2/с2.
Средняя кинетическая энергия поступательного движения молекулы:
Давление идеального газа пропорционально концентрации молекул и средней кинетической энергии их поступательного движения.
Абсолютная температура
Термодинамическое (тепловое) равновесие – состояние тела или системы тел, при котором все макроскопические параметры (давление, объем, температура, масса) остаются неизменными сколь угодно долго.
Температура – термодинамический параметр, который одинаков во всех частях термодинамической системы.
Температура – скалярная физическая величина, характеризующая состояние термодинамического равновесия системы и являющаяся мерой кинетической энергии поступательного движения молекул (атомов) тела.
Основой измерения температуры является зависимость какого-либо свойства тела (например объема или электрического сопротивления) от температуры. На практике чаще всего встречаются термометры, в которых используется зависимость объема жидкости (спирт, ртуть) от температуры. Для измерения температуры необходимо привести тело в тепловой контакт с термометром. Показания термометра следует отсчитывать только после наступления теплового равновесия с термометром. Масса термометра должна быть намного меньше массы тела, температуру которого измеряют.
На практике распространена температурная шкала Цельсия. Она строится по двум опорным (реперным) точкам: температуре таяния льда и температуре кипения воды, которым приписаны температуры \( t_{пл.} \) = 0 °С и \( t_{к.в.} \) = 100 °С. Недостаток этой шкалы, как и остальных температурных шкал, – произвольный выбор опорных точек и их зависимость от внешних условий.
От этого недостатка свободна абсолютная шкала температур. Принцип создания этой шкалы заключается в следующем. Кинетическая энергия молекул может быть больше или равна нулю. Температура, при которой прекращается хаотическое поступательное движение молекул, называется абсолютным нулем. Этому значению соответствует температура –273,15 °С.
Шкала температур, на которой температура отсчитывается от абсолютного нуля, а деления равны градусам шкалы Цельсия, называется абсолютной температурной шкалой, или шкалой Кельвина. На такой шкале не существует отрицательных температур.
Обозначение – \( T \), единица измерения в СИ – кельвин (К).
Кельвин является одной из основных единиц Международной системы единиц. Перевод температуры \( t \) из градусов Цельсия в температуру \( T \) в кельвинах:
Перевод температуры \( T \) из кельвинов в температуру \( t \) в градусах Цельсия:
Важно!
При решении задач нужно помнить, что температура всегда переводится в кельвины. Один градус по шкале Цельсия и один кельвин равны. Поэтому любое значение абсолютной температуры будет на 273 градуса выше соответствующей температуры в градусах Цельсия. Но изменение абсолютной температуры равно изменению температуры в градусах Цельсия: \( \Delta T=\Delta t \).
Связь температуры газа со средней кинетической энергией его частиц
Температура – характеристика внутреннего состояния макроскопической системы – состояния теплового равновесия.
Важно!
Температура – термодинамический параметр, одинаковый во всех частях термодинамической системы, находящейся в тепловом равновесии. Температуры тел, находящихся в тепловом контакте, выравниваются.
Опытным путем было установлено, что при тепловом равновесии отношение давления к концентрации для всех газов одинаково. То есть отношение
обладает свойствами температуры. Но здесь возникает неудобство, связанное с тем, что единица измерения \( \Theta \) – джоуль, а температуру традиционно измеряют в градусах. Поэтому отношение давления к концентрации считают пропорциональным абсолютной температуре:
Коэффициент пропорциональности называется постоянной Больцмана. Эта постоянная связывает температуру в энергетических единицах (джоулях) с температурой в кельвинах:
Числовое значение постоянной Больцмана \( k=1.38\cdot10^{-23} \) Дж/К. Тогда основное уравнение МКТ можно записать так:
Из этого уравнения следует, что давление газа пропорционально концентрации молекул и абсолютной температуре. Используя запись этого уравнения, через среднюю кинетическую энергию частицы \( E \) можно получить соотношение между средней кинетической энергией и температурой:
Абсолютная температура является величиной, прямо пропорциональной средней кинетической энергии теплового движения частиц.
Для скорости частицы можно записать формулу:
где \( m_0 \) – масса частицы, \( M \) – молярная масса, \( R \) – универсальная газовая постоянная.
Уравнение p=nkT
Основное уравнение МКТ, используя понятие абсолютной температуры, можно записать так:
Из этой формулы следует, что при одинаковых давлениях и температурах концентрация молекул у всех газов одинакова. В равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число частиц (закон Авогадро).
Уравнение Менделеева – Клапейрона
Уравнение, устанавливающее связь между макропараметрами газа массой \( m \), давлением \( p \), объемом \( V \) и температурой \( T \), называется уравнением состояния идеального газа.
Клапейрон установил, что при постоянной массе газа отношение произведения давления газа на объем к его абсолютной температуре остается постоянным:
Это одна из форм записи уравнения состояния идеального газа. Если газ взят в количестве одного моля при нормальном атмосферном давлении и температуре 273 К, то его объем равен 0,0224 м3. Тогда отношение
Эту величину обозначают \( R \) и называют универсальной газовой постоянной:
Тогда уравнение Клапейрона для 1 моль идеального газа запишется так:
Для количества вещества, равного любому числу моль:
В такой форме уравнение состояния идеального газа впервые было записано Д. И. Менделеевым. Эту формулу называют уравнением Менделеева – Клапейрона.
Изопроцессы: изотермический, изохорный, изобарный, адиабатный процессы
Изопроцесс — это процесс, протекающий при постоянной массе газа и постоянном значении одного из параметров состояния системы.
Изотермический процесс — термодинамический процесс, проходящий при постоянной температуре и неизменной массе газа.
Изотермический процесс подчиняется закону Бойля – Мариотта: для данной массы газа при неизменной температуре произведение числовых значений давления и объема постоянно:
Важно!
Процесс можно считать изотермическим, если он протекает медленно. Например, подъем воздушного пузырька со дна пруда к поверхности.
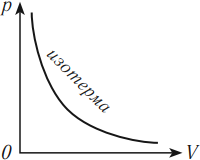
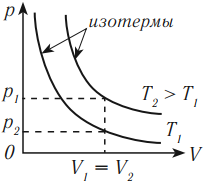
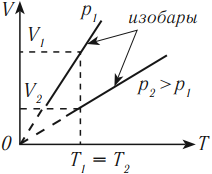
На графике изотермический процесс изображается кривой, которую называют изотерма.
Разным температурам соответствуют разные изотермы. При одинаковых объемах газ с более высокой температурой производит большее давление. Значит, чем выше температура, тем выше расположена изотерма в осях \( (p,V) \).
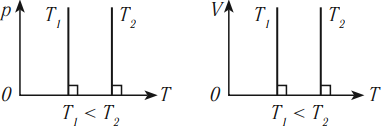
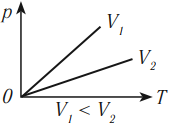
В координатных осях \( p(T) \) и \( V(T) \) график изотермического процесса выглядит так:
Изобарный процесс — термодинамический процесс, проходящий при неизменной массе газа и постоянном давлении.
Изобарный процесс подчиняется закону Гей-Люссака: при неизменном давлении объем данной массы газа прямо пропорционален его абсолютной температуре:
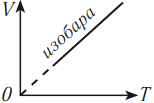
На графике зависимости объема от температуры этот процесс изображается прямой, которую называют изобара. Изобара всегда выходит из начала координат в осях \( (V, T) \).
Так как абсолютный нуль недостижим, то из начала координат изобару проводят пунктиром.
Разным давлениям соответствуют разные изобары. При одинаковой температуре чем меньше объем газа, тем большее давление он производит. Это значит, что, чем выше давление, тем ниже расположена изобара в осях \( (V, T) \).
В координатных осях \( p(T) \) и \( p(V) \) график изобарного процесса выглядит так:
Важно!
Процесс можно считать изобарным, если не меняется внешнее давление.
Изохорный процесс – это термодинамический процесс, проходящий при неизменной массе газа и постоянном объеме.
Изохорный процесс подчиняется закону Шарля: при неизменном объеме давление данной массы газа прямо пропорционально его абсолютной температуре:
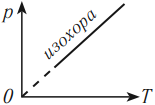
На графике зависимости давления от температуры этот процесс изображается прямой, которую называют изохора. Изохора всегда выходит из начала координат в осях \( (p, T) \). Так как абсолютный нуль недостижим, то из начала координат изохору проводят пунктиром.
Разным объемам соответствуют разные изохоры. При одинаковой температуре чем меньше объем газа, тем большее давление он производит. Поэтому при одинаковой температуре чем больше объем, тем ниже расположена изохора (в осях \( p,V \)).
В координатных осях \( V(T) \) и \( p(V) \) график изобарного процесса выглядит так:
Важно!
Процесс можно считать изохорным, если он происходит в закрытом сосуде.
Адиабатный процесс – термодинамический процесс, проходящий без теплообмена с окружающей средой.
Адиабатный процесс возможен при хорошей теплоизоляции системы. К адиабатным можно отнести быстро протекающие процессы сжатия или расширения газа. При быстром сжатии газа затрачивается работа, приводящая к увеличению внутренней энергии и повышению температуры. Тело, температура которого повышена, должно некоторое количество теплоты передать окружающей среде, но процесс теплопередачи требует некоторого времени, поэтому при быстром сжатии (или расширении) теплота не успевает распространиться из данного объема (\( Q \) = 0), и процесс можно рассматривать как адиабатный.
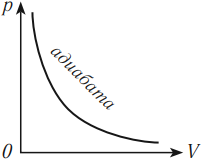
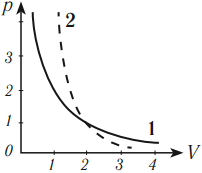
Зависимость давления от объема газа при адиабатном процессе на графике изображается кривой, называемой адиабата. При адиабатном сжатии давление газа с уменьшением объема растет быстрее из-за повышения температуры. Различие в изображении адиабаты и изотермы дает рисунок, на котором адиабата обозначена цифрой 2, а изотерма – цифрой 1.
Примером адиабатного процесса в природе является образование облаков.
При решении задач на «Уравнение Менделеева – Клапейрона» и газовые законы выделяют следующие группы задач:
- Переход идеального газ из одного состояния в другое без изменения массы.
- Состояние газа не меняется, а масса изменяется.
- Изменяется и масса и состояние газа.
Алгоритм решения задач первой группы:
- установить, какой газ участвует в том или ином процессе;
- определить параметры p, V и T, характеризующие каждое состояние газа;
- записать уравнение объединенного газового закона Клапейрона для данных состояний; если один из трех параметров остается неизменным, уравнение Клапейрона автоматически переходит в одно из трех уравнений газовых законов;
- записать математически все вспомогательные условия;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Алгоритм решения задач второй группы:
- установить, какие газы участвуют в рассматриваемых процессах;
- определить параметры p, V и T, характеризующие каждое состояние газа;
- для каждого состояния каждого газа (если их несколько) составить уравнение Менделеева – Клапейрона. Если дана смесь газов, то это уравнение записывается для каждого компонента. Связь между значениями давлений отдельных газов и результирующим давлением смеси устанавливается законом Дальтона;
- записать математически дополнительные условия задачи;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Алгоритм решения задач третьей группы:
- внимательно проанализировать условие задачи и исходные данные;
- установить, какие параметры газа изменяются, а какие остаются постоянными;
- обратить внимание на параметры, заданные неявно;
- записать для каждого состояния газа уравнение Менделеева – Клапейрона;
- записать математически дополнительные условия задачи;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Насыщенные и ненасыщенные пары
При испарении жидкости в закрытом сосуде через некоторое время количество жидкости перестает уменьшаться, хотя молекулы продолжают переходить в пар. В этом случае наряду с процессом парообразования происходит процесс превращения пара в жидкость – конденсация. Это означает, что жидкость и ее пар находятся в состоянии динамического равновесия, когда число молекул, вылетающих из жидкости, равно числу молекул, возвращающихся в жидкость из пара. В состоянии динамического равновесия скорости процессов испарения и конденсации одинаковы. С этого момента количество жидкости и ее пара не меняется. Пар, находящийся в равновесии со своей жидкостью, называют насыщенным.
При повышении температуры давление насыщенного пара и его плотность возрастают, а плотность жидкости уменьшается из-за теплового расширения. Температура, при которой исчезают физические различия между жидкостью и ее паром, называется критической \( T_{кр.} \). При температуре, равной критической температуре \( T_{кр.} \) для данного вещества, плотности пара и жидкости становятся одинаковыми. При \( T \geq T_{кр.} \) исчезают физические различия между жидкостью и ее насыщенным паром.
Свойства насыщенного пара
Давление насыщенного пара данной жидкости при постоянной температуре – постоянная величина, и она не зависит от объема пространства над испаряющейся жидкостью. Значит, при постоянной температуре плотность насыщенного пара постоянна.
- Давление и плотность насыщенных паров у различных жидкостей при одной и той же температуре различны. У летучих жидкостей они больше.
- Давление насыщенных паров – наибольшее возможное давление паров данной жидкости при данной температуре.
- Наличие других газов над испаряющейся жидкостью не влияет на давление и плотность насыщенного пара данной жидкости, а только замедляет процесс испарения.
- Давление насыщенного пара \( p_{нас.} \) данного вещества зависит только от его температуры и не зависит от объема.
Число молекул, вылетающих с единицы площади поверхности жидкости за одну секунду, зависит от температуры жидкости. Число молекул, возвращающихся из пара в жидкость, зависит от концентрации молекул пара и от средней скорости их теплового движения, которая определяется температурой пара. Отсюда следует, что для данного вещества концентрация молекул пара при равновесии жидкости и ее пара определяется их температурой. Установление динамического равновесия между процессами испарения и конденсации при повышении температуры происходит при более высоких концентрациях молекул пара.
Так как давление газа (пара) определяется его концентрацией и температурой, то можно сделать вывод: давление насыщенного пара \( p_{нас.} \) данного вещества зависит только от его температуры и не зависит от объема.
Если изотермически сжимать ненасыщенный пар \( (T < T_{кр.}) \), то его давление будет возрастать, пока не станет равным давлению насыщенного пара. При дальнейшем уменьшении объема на дне сосуда образуется жидкость и устанавливается динамическое равновесие между жидкостью и ее насыщенным паром. С уменьшением объема все большая часть пара конденсируется, а его давление остается неизменным. Когда весь пар превращается в жидкость, давление резко возрастает при дальнейшем уменьшении объема вследствие малой сжимаемости жидкости.
Давление насыщенного пара не зависит от объема при данной температуре. Если объем изменяется, то конденсация будет преобладать над испарением или наоборот, пока не установится динамическое равновесие.
Давление \( p_{нас.} \) насыщенного пара очень быстро возрастает с ростом температуры \( T \). Зависимость \( p_{нас.}(T) \) нельзя получить из законов идеального газа. Давление газа при постоянной концентрации молекул растет прямо пропорционально температуре. В насыщенном паре при повышении температуры возрастает не только средняя кинетическая энергия движения молекул, но и их концентрация. Поэтому давление насыщенного пара при повышении температуры возрастает быстрее, чем давление идеального газа при постоянной концентрации молекул.
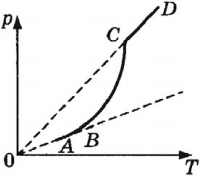
На рисунке показана зависимость давления насыщенного пара от температуры. На участке АВ (в сосуде пар и жидкость) давление увеличивается за счет роста температуры и, соответственно, скорости частиц. На участке ВС (в сосуде пар и жидкость) давление увеличивается как за счет роста температуры, так и за счет увеличения концентрации молекул пара. Участок СD (в сосуде только пар) соответствует состоянию, когда давление растет за счет увеличения скоростей молекул пара.
Зависимость между массой, объемом, давлением и температурой для насыщенного пара не такая, как для идеального газа, так как если пар в каком-либо процессе остается насыщенным, то его масса меняется. При изотермическом сжатии насыщенный пар частично конденсируется, так что его давление остается постоянным. При изохорном охлаждении насыщенный пар частично конденсируется, его давление уменьшается и становится равным давлению насыщенного пара при более низкой температуре.
Ненасыщенный пар можно теоретически описывать с помощью уравнения состояния идеального газа при обычных для реальных газов ограничениях: давление пара должно быть не слишком велико (практически \( p \) ≤ (106–107) Па), а его температура выше некоторого определенного для каждого вещества значения. К насыщенному пару также можно приближенно применять законы идеального газа.
Влажность воздуха
Влажность воздуха – физическая величина, характеризующая содержание водяного пара в воздухе. Различают абсолютную и относительную влажность.
Абсолютная влажность – физическая величина, равная массе водяных паров, содержащихся в 1 м3 воздуха при данных условиях. Обычно ее вычисляют не в единицах СИ, а в г/м3. В метеорологии абсолютную влажность оценивают по давлению водяного пара, выраженному в миллиметрах ртутного столба.
Относительной влажностью называют отношение абсолютной влажности к тому количеству водяного пара, которое необходимо для насыщения 1 м3 воздуха при данной температуре.
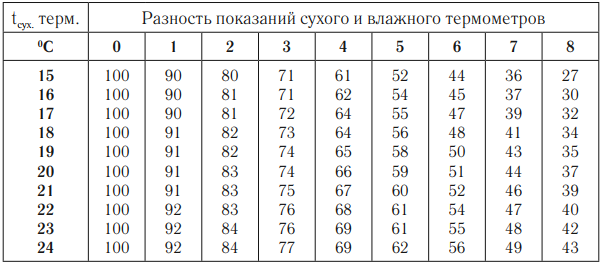
Обозначение – \( \varphi \), единица измерения – %.
Относительная влажность показывает, насколько водяной пар, содержащийся в воздухе, близок к насыщению. Формула для вычисления относительной влажности:
где \( p_{пар} \) –парциальное давление водяного пара воздуха при данной температуре, \( p_{нас} \) – давление насыщенного пара при той же температуре.
От относительной влажности зависит интенсивность испарения и потеря влаги живыми организмами. Комфортной для человека является влажность 40–60%.
Точкой росы называется температура, при которой водяной пар, содержащийся в воздухе, становится насыщенным.
Для измерения влажности используют:
- психрометр, основанный на зависимости влажности от скорости испарения воды;
- гигрометр, основанный на использовании температуры выпадения росы при охлаждении воздуха (определение точки росы);
- волосяной гигрометр, основанный на удлинении волоса при изменении влажности;
- электронный измеритель влажности, основанный на изменении сопротивления полупроводника при изменении влажности.
Психрометр состоит из двух термометров – сухого, который показывает температуру воздуха, и влажного, резервуар которого обмотан влажной тканью. По психрометрической таблице выбирают строку, соответствующую показаниям сухого термометра, и столбец, соответствующий значению разности температур сухого и влажного термометров. На пересечении строки и столбца – значение относительной влажности воздуха.
Гигрометр дает определение влажности по точке росы. Определив точку росы и зная температуру воздуха, по таблице зависимости давления насыщенного водяного пара от температуры вычисляют абсолютную влажность воздуха.
Изменение агрегатных состояний вещества: испарение и конденсация, кипение жидкости
Любое вещество при определенных условиях может находиться в различных агрегатных состояниях – твердом, жидком и газообразном. Переход из одного состояния в другое называется фазовым переходом.
Парообразование – это процесс перехода вещества из жидкого состояния в газообразное.
Испарением называется парообразование, происходящее с поверхности жидкости при любой температуре.
Молекулы, вылетевшие из жидкости при парообразовании, называются паром данной жидкости. Поверхность жидкости покидают молекулы с наибольшей скоростью (соответственно и кинетической энергией), поэтому в результате испарения температура жидкости уменьшается. Скорость испарения зависит от рода жидкости, температуры, площади поверхности жидкости и отвода вылетевших молекул.
Конденсация – это процесс, обратный процессу испарения. При конденсации молекулы пара возвращаются в жидкость.
Кипением называется процесс интенсивного парообразования, происходящий по всему объему жидкости.
В жидкости всегда имеются мельчайшие пузырьки пара. Пар внутри пузырька является насыщенным. При повышении температуры жидкости давление пара в пузырьке возрастает и его объем увеличивается. Под действием архимедовой силы пузырек всплывает на поверхность. Если давление насыщенного пара внутри пузырька равно внешнему давлению, то жидкость кипит.
Важно!
Кипение жидкости начинается при такой температуре, при которой давление ее насыщенных паров становится равным внешнему давлению.
Температурой кипения называется температура жидкости, при которой давление ее насыщенного пара равно внешнему давлению.
Температура кипения повышается с ростом внешнего давления и понижается при его уменьшении. При нормальном атмосферном давлении вода кипит при температуре 100 °С. Это значит, что при такой температуре давление насыщенных паров воды равно 1 атм или 105 Па. При подъеме в горы атмосферное давление уменьшается, и поэтому температура кипения воды понижается (приблизительно на 1 °С на каждые 300 м высоты). На высоте 7 км давление составляет примерно 0,4 атм и температура кипения понижается до 70 °С.
Важно!
В герметически закрытом сосуде жидкость кипеть не может, т. к. при каждом значении температуры устанавливается равновесие между жидкостью и ее насыщенным паром.
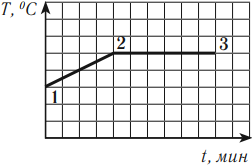
В процессе кипения температура жидкости остается постоянной (если не изменяется внешнее давление). На графике можно увидеть, что участок 1–2 — это нагревание жидкости, участок 2–3 — кипение. Подводимое к жидкости тепло расходуется на парообразование.
Количество теплоты, необходимое для превращения жидкости, нагретой до температуры кипения, в пар, вычисляется по формуле:
где \( L \) – удельная теплота парообразования вещества, \( m \) – масса вещества.
Удельная теплота парообразования вещества – это физическая величина, равная количеству теплоты, необходимому для превращения 1 кг жидкости при постоянной температуре в пар.
Единица измерения удельной теплоты парообразования в СИ – Дж/кг.
При конденсации пара выделяется такое же количество теплоты:
Изменение агрегатных состояний вещества: плавление и кристаллизация
Плавление – процесс перехода вещества из твердого состояния в жидкое.
Чтобы происходило плавление твердого тела, к нему необходимо подводить тепло. Плавление твердого тела происходит при определенной температуре, называемой температурой плавления. Температура плавления зависит от внешнего давления.
При плавлении амплитуда колебаний частиц, находящихся в узлах кристаллической решетки, увеличивается и становится сравнимой с расстоянием между частицами. Притяжение частиц вещества становится слабее. В результате в процессе плавления происходит разрушение кристаллической решетки. В процессе плавления твердое тело существует одновременно в твердом и жидком состояниях. При плавлении температура тела не меняется и равна температуре плавления.
Для того чтобы расплавить вещество, к нему необходимо подводить тепло. Количество теплоты, необходимое для плавления, вычисляется по формуле:
где \( \lambda \) – удельная теплота плавления вещества, \( m \) – масса вещества.
Удельная теплота плавления вещества – это физическая величина, равная количеству теплоты, необходимому для превращения 1 кг кристаллического вещества при температуре плавления в жидкость той же температуры.
Единица измерения в СИ – Дж/кг.
Кристаллизация (отвердевание) – переход вещества из жидкого состояния в твердое.
Кристаллизация происходит при постоянной температуре, равной температуре плавления. Кристаллизация начинается вблизи центров кристаллизации – примесей, пылинок. Около них начинается упорядочение структуры в расположении частиц и образование кристаллической решетки. Кристаллизация сопровождается выделением тепла:
Изменение энергии в фазовых переходах
Все вещества могут находиться в трех агрегатных состояниях (фазах): газообразном, жидком и твердом. Возможен переход вещества из одного агрегатного состояния (фазы) в другое. Такие переходы называют фазовыми переходами.
Фазовый переход – это переход вещества из одной фазы в другую при изменении внешних условий (температуры, давления), сопровождающийся скачкообразным изменением его физических свойств.
Выделяют следующие фазовые переходы: плавление и кристаллизация, парообразование и конденсация.
Важно!
Переход вещества из одной фазы в другую при постоянном давлении происходит при строго определенной температуре. Внутренняя энергия при фазовых переходах изменяется.
Для плавления требуется сообщить телу некоторое количество теплоты. При нагревании вещества до температуры плавления подводимая энергия идет на увеличение скорости движения частиц. Это значит, что при нагревании до температуры плавления растут температура вещества и его внутренняя энергия. Подводимая к телу энергия в процессе плавления идет на работу по преодолению сил межмолекулярного притяжения. Это связано с увеличением средних расстояний между частицами вещества при переходе из твердого состояния в жидкое. Скорость движения частиц при этом не изменяется, поэтому остается постоянной и температура вещества.
Внутренняя энергия увеличивается за счет увеличения потенциальной энергии взаимодействия частиц, а кинетическая энергия частиц не меняется. Вещество в жидком состоянии обладает большей внутренней энергией, чем в твердом.
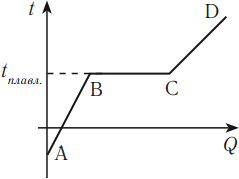
График зависимости температуры кристаллического тела от полученного количества теплоты выглядит следующим образом.
На этом графике участок АВ соответствует нагреванию кристаллического тела, участок ВС – плавлению, участок CD – нагреванию жидкости.
При понижении температуры вещества до температуры плавления происходит кристаллизация – переход вещества из жидкой фазы в твердую фазу. При кристаллизации выделяется количество теплоты, равное поглощаемому при плавлении. В процессе кристаллизации температура остается постоянной. Происходит восстановление межмолекулярных связей и кристаллической решетки.
Внутренняя энергия при кристаллизации уменьшается. Если тело отдает количество теплоты, то участок графика DC соответствует охлаждению жидкости, участок СВ – кристаллизации, участок ВА – охлаждению кристаллического тела.
Для осуществления процесса кипения к жидкости нужно подводить тепло. При нагревании до температуры кипения растет температура жидкости и ее внутренняя энергия за счет увеличения скорости молекул жидкости.
При кипении температура жидкости не изменяется, а внутренняя энергия растет за счет увеличения потенциальной энергии взаимодействия частиц (расстояния между частицами увеличиваются). Кинетическая энергия частиц остается постоянной. При конденсации внутренняя энергия молекул пара уменьшается, так как потенциальная энергия уменьшается (кинетическая энергия частиц не меняется).
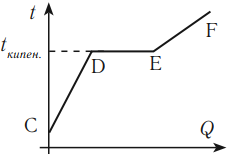
График зависимости температуры жидкости от полученного или отданного количества теплоты выглядит следующим образом.
На графике участок CD соответствует нагреванию жидкости, участок DE – кипению, участок EF – нагреванию пара.
Если тело отдает количество теплоты, то участок FE соответствует охлаждению пара, участок ED – конденсации, участок DC – охлаждению жидкости.






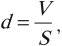
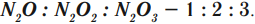
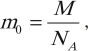
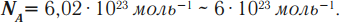
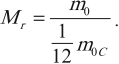
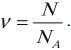
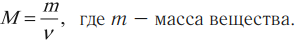
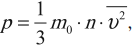
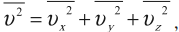
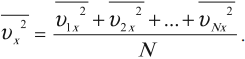
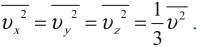
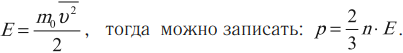
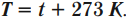
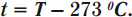
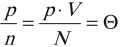
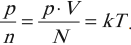
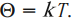
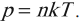
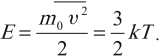
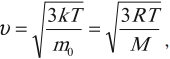
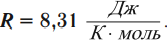
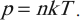
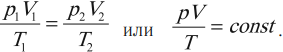
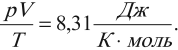
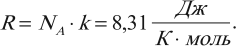
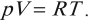
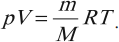
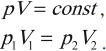
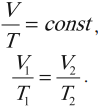
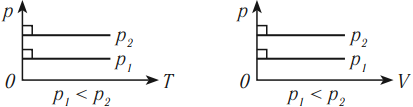
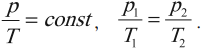
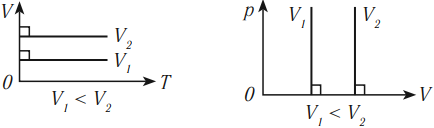
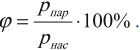
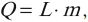
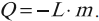
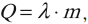
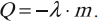


Добавить комментарий
я в рот ебала физичку мамонтиха сраная
мой отец насиловал меня в детстве
Нет, это меня он насиловал, а вас с мамой он никогда не любил
я продаю оружие и наркотики
А как мефедрон то сварить
бля ненавижу физику ща пополню баланс на скайпе и пизда этому техникуму
Я ЕБАЛ ФИЗРУКА.Я ЕМУ УЖЕ ПИВО ДАЖЕ ПОДОГНАЛ А ОН ВСЁ АТТЕСТАЦИЮ НЕ СТАВИТ.Не могу я пробежать круг без бургера в руках.
А я пацаны дома апельсин ебу,делаю дырку в нем и сую свой писюнчик,а после сьедаю,по вкусу напоминает хурму
Парни,честно я лизал пизду химички😝😝😝😝
АХ АХ ВСУНЬ В МЕНЯ СВОЮ КНИЖКУ ФИЗИКИ ОРГАЗМ YEAAASSSAYATATSGSTSGGSGSGS
У меня член 10 см,думаю не маленький,че думаете пацаны??
че делать если писюн не растет, устал уже мизинцем дрлчить
В ЖОПУ МЕНЯ ТРАХНИТЕ АААА СЕКС НАРКОТИКИ МЕФЕДРОН КАК ЖЕ КАЙФОВО ДОЛБИТЬСЯ В ЖОПУ АААА
я в рот ебал вашу физику идите нахуй с ней, физик чмо ебанное, душнила нахуй
бляя, я на нашу математичку подрачиваю, как возбуждает
Крч, бухал вчера, блевал пиздец , успел подрочить на физичку и химичку
Я химичку в рот ебал, заебала, меня говном обозвала и ещё товар требует,
Ахуеть пацаны,я на физичку Машу дрочу
Вы офигели? Кто от моего имени пишет тут плохие вещи, про эту мымру
не суетись
Я эту Кашицину вертел и её английский, я ей мерс обоссу
Парни я устал писать, скажите ему чтобы он нас отпустил